Общие понятия РЕКУРСИЯ

 Общие понятия РЕКУРСИЯ

Рекурсивным называют метод, если он вызывает сам себя в каче- стве вспомогательного. В основе рекурсивного метода лежит так назы- ваемое рекурсивное определение какого-либо понятия. Классическим примером рекурсивного метода является метод, вычисляющий факто- риал.

Из курса математики известно, что 0!=1!=1, n!=1*2*3…*n. С дру- гой стороны n!=(n-1)!*n. Таким образом, известны два частных случая параметра n, а именно n= 0 и n=1, при которых мы без каких-либо до- полнительных вычислений можем определить значение факториала. Во всех остальных случаях, то есть для n>1, значение факториала может быть вычислено через значение факториала для параметра n-1. Таким образом, рекурсивный метод будет иметь вид:

long F(int n)

{

// Дошли до 0 или 1? if (n == 0 || n == 1)

// Нерекурсивная ветвь return 1;

else

// Шаг рекурсии: повторный вызов

// метода с другим параметром return n * F(n - 1);

}

// Пример вызова рекурсивного метода

long f = F(3); MessageBox.Show(f.ToString());

Рассмотрим работу описанного выше рекурсивного метода для n=3.

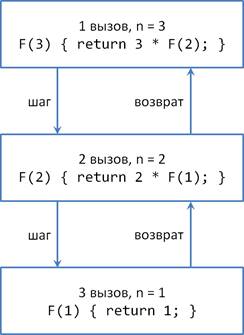Рис. 14.1. Структура рекурсивных вызовов

Первый вызов метода осуществляется из основной программы, в нашем случае командой f = F(3). Этап вхождения в рекурсию обозна- чим стрелками с подписью «шаг». Он продолжается до тех пор, пока значение переменной n не становится равной 1. После этого начинается выход из рекурсии (стрелки с подписью «возврат»). В результате вы- числений получается, что F(3) = 3 * 2 * 1.

Рассмотренный вид рекурсии называют прямой. Метод с прямой рекурсией обычно содержит следующую структуру:

if (<условие>)

<оператор>;

else

<вызов этого же метода с другими параметрами>;

В качестве <условия> обычно записываются некоторые граничные случаи параметров, передаваемых рекурсивному методу, при которых результат его работы заранее известен, поэтому далее следует простой

оператор или блок, а в ветви else происходит рекурсивный вызов дан- ного метода с другими параметрами.

Что необходимо знать для реализации рекурсивного процесса? Со входом в рекурсию осуществляется вызов метода, а для выхода необхо- димо помнить точку возврата, т. е. то место программы откуда мы при- шли и куда нам нужно будет возвратиться после завершения метода. Место хранения точек возврата называется стеком вызовов и для него выделяется определенная область оперативной памяти. В этом стеке за- поминаются не только адреса точек возврата, но и копии значений всех параметров. По этим копиям восстанавливается при возврате вызываю- щий метод. При развертывании рекурсии за счет создания копий пара- метров возможно переполнение стека. Это является основным недо- статком рекурсивного метода. С другой стороны, рекурсивные методы позволяют перейти к более компактной записи алгоритма.

Следует понимать, что любой рекурсивный метод можно преобра- зовать в обычный метод с использованием циклов. И практически лю- бой метод можно преобразовать в рекурсивный, если выявить рекур- рентное соотношение между вычисляемыми в методе значениями.

Рассмотрим пример кода для создания набора самоподобных структур. В нашем случае это будет набор увеличивающихся квадра- тов (рис. 14.2).

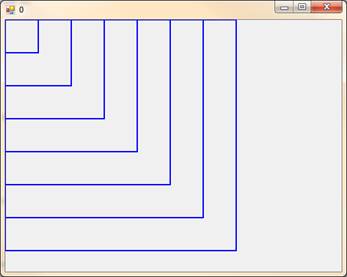Рис. 14.2. Набор квадратов

При проектировании данной программы были созданы два метода:

private void MyDraw(Graphics g, int N, int x, int y)

{

if (N == 0)

return;

else

{

}

}

// Отрисовка прямоугольника g.DrawRectangle(new Pen(Brushes.Blue, 2),

0, 0, x, y);

// Увеличение x и y на 50 x += 50;

y += 50; N--;

// Рекурсивный вызов с новыми параметрами MyDraw(g, N, x, y);

private void Form1_Paint(object sender, PaintEventArgs e)

{

Graphics g = e.Graphics;

// Первый вызов метода и вход в рекурсию MyDraw(g, 7, 50, 50);

}

Координаты левого верхнего угла всех прямоугольников неизмен- ны и находятся в точке (0, 0). Поэтому в параметрах метода MyDraw до- статочно передавать x и y для правого нижнего угла. Также в парамет- рах передается N, значение которой определяет текущую вложенность рекурсии (сколько вызовов рекурсии еще будет).