ОДНОЧЛЕНЫ И ЕГО СТАНДАРТНЫЙ ВИД

Одночлены и его стандартный вид

Цели: ввести понятие одночлена и его стандартного вида; формировать умение приводить одночлен к стандартному виду путем его упрощения; формировать умение определять коэффициент и степень одночлена.

Ход урока

I. Устная работа.

1. Упростите выражение.

а) х³ · (–х⁴);                                б) х³ · (–х)⁴;                                       в) (–х)³ · х⁴;

г) (–х³) · (–х)⁴;                                          д) (а²)⁵ · а⁵;                                        е) (а² · а⁵)².

2. Выполняя задания на преобразование выражений, содержащих степени, ученик допустил следующие ошибки:

а) 5 · 5 · 5 · 5 = 4⁵;        б) (–3)² = –3 · 3 = –9;                      в) 7¹ = 1;

г) 0⁰ = 1;                                          д) 2³ · 2⁷ = 2²¹;                                                   е) 2³ · 2⁸ = 4¹⁰;

ж) 2³ + 2⁷ = 2¹⁰;             з) 2³⁰ : 2¹⁰ = 2³;                                                  и) (2х)³ = 2х³;

к) (а³)² = а⁹;                                   л) (а²)³ · (а⁴)² = (а⁶)⁵ = а³⁰.

Какие определения, свойства, правила не знает ученик?

II. Объяснение нового материала.

1. При решении различных задач часто встречаются алгебраические выражения вида  a · b;   · a · b · c;  3 · a² · b. Для сокращения записи этих выражений знак умножения «точка» обычно опускается, то есть пишут просто  ab;  abc;  3a²b.  Каждое  из  этих  произведений  называют одночленом.

На доску выносится запись:

Например, одночленами являются выражения:

abc;     (–4)a3ab;     a(–0,3)bab;     172;     –.

Так как произведение равных множителей можно записать в виде степени с натуральным показателем, то степень числа и произведение степеней чисел также называют одночленами.

Например:  ;     (–7)³;     c⁵;     4a²; 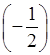    a²b.

Множители одночлена, записанные с помощью цифр, называют числовыми множителями одночлена, а множители, обозначенные буквами, называют буквенными множителями.

2. Одночлены можно упрощать, пользуясь переместительным и сочетательным законами умножения.

Обращаем внимание учащихся, что коэффициент одночлена может быть  равен  единице,  в  этом  случае  мы  его  не  пишем  перед  буквенной частью. Переменные принято записывать в алфавитном порядке, то есть не 3x²a⁴c, а 3a⁴cx².

3. Вводим понятие степени одночлена.

III. Формирование умений и навыков.

На этом занятии необходимо отработать следующие умения:

1) выявлять одночлен, используя определения;

2) выделять элементы одночлена: числовой коэффициент и буквенную часть;

3) определять, записан ли одночлен в стандартном виде;

4) приводить одночлен к стандартному виду;

5) вычислять значение одночлена в стандартном виде;

6) определять степень одночлена стандартного вида.

1. (Устно). Назовите числовые и буквенные множители одночлена.

а) 6a(0,3)b2c;                                           в) 3p(–0,1)q7r;  б) 0,5ab3c;                                   г) 2,5mn4k.

2. № 455 (устно).

3. Вместо  словесной  формулировки  запишите  алгебраическое  выражение:

а) удвоенное произведение чисел a и b;

б) утроенное произведение чисел b и с;

в) произведение квадратов чисел х и у;

г) произведение числа а и квадрата числа b;

д) произведение куба числа т и числа р;

е) утроенное произведение квадрата числа а и числа b.

4. № 456 (устно).

При выполнении этого упражнения ученики должны мотивировать свой ответ.

5. Среди одночленов  10,2a²b²c;  –7,3ab²c;  17a²bca;  –2,6ab²c;  –m;  3ab; –28a²b²c²;  3aabc;  –2ab;  –m⁴m;  m ∙  2;  17a²b²c²:

а) назвать одночлены стандартного вида;

б) указать одночлены, отличающиеся только коэффициентами.

6. № 457.

Решение:

а) 8x²x = 8x^{2 + 1} = 8x³; б) 1,2abc ∙  5a = (1,2 ∙  5) ∙  (a ∙  a) ∙  bc = 6a²bc;

в) 3xy(–1,7)y = 3 ∙  (–1,7) ∙  x ∙  y ∙  y = –5,1xy²; г) 6c²(–0,8)c = 6(–0,8)c²c = –4,8c³;

д) m²n ∙  4,5n³ =  ∙  m² ∙  n ∙  n³ = 3m²n⁴; е) 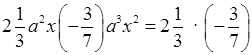 a²a³xx² = –a⁵x³.

7. № 459.

Решение:

а) если у = –2, то –0,125у⁴ = –0,125 · (–2)⁴ = –0,125 · 16 = –2;

б) если х = –0,3, у = , то 12x²y = 12 · (–0,3)² · = 2 · 0,09 = 0,18.

Ответ: а) –2;  б) 0,18.

8. № 461.

Решение:

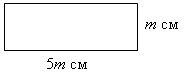                         S = 5m · m = 5m² (см²).

Ответ: 5m² (см²).

9. Запишите одночлен в стандартном виде и определите его степень.

а) ac12c;                                                     г)  · 4; б) a8b²ba³;                       д) –m³np;

в) –0,5xy²x³;                                        е) a³d0x.

IV. Итоги урока.

Домашнее задание: № 458; № 460; № 462; № 463; № 554; № 555.