
Олимпиада по математике
для учащихся 7 классов
Школьный этап
(2022/23учебный год)
Пояснительная записка
Цели олимпиады по математике:
· овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин.
· интеллектуальное развитие, формирование умений точно, грамотно, аргументировано излагать мысли овладение методами поиска, систематизации, анализа, классификации информации
· формирование представлений об идеях и методах математики как средства моделирования явлений и процессов;
· воспитание отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
Тематика заданий:
1. Арифметические преобразования.
2. Решить уравнение на понятие модуля.
3. Логическая задача.
4. Логическая задача.
5. Логическая задача на числа.
6. Геометрическая задача.
7. Задача на проценты.
Рекомендуемое время: 135мин
Критерии оценивания:
|
Число баллов |
4 |
5 |
6 |
|
Безупречное решение |
4 |
5 |
6 |
|
Решение с недочетами |
3 |
4 |
5 |
|
Неполное решение с негрубыми ошибками |
2 |
3 |
4 |
|
Неверное решение, но есть продвижение в верном направлении |
1 |
2 |
3 |
|
Отсутствие решения |
0 |
0 |
0 |
При оценивании олимпиадных заданий жюри следует учитывать, что:
а) любое правильное решение оценивается в максимальное колличество баллов. Недопустимо снятие баллов за то, что решение слишком длинное, или за то, что решение школьника отличается от приведенного в методических разработках или от других решений, известных жюри;
б) олимпиадная работа не является контрольной работой обучающегося, поэтому любые исправления в работе, в том числе зачеркивание ранее написанного текста, не являются основанием для снятия баллов;
в) баллы не выставляются «за старание Участника», в том числе за запись в работе большого по объему текста, но не содержащего продвижений в решении задачи;
г) победителями олимпиады в одной параллели могут стать несколько участников, набравшие наибольшее количество баллов, поэтому не следует в обязательном порядке «разводить по местам» лучших участников олимпиады.
Подведение итогов:
I место присуждается всем участникам, набравшим больше 75 % от максимального числа баллов за все задания олимпиады. ( При необходимости опустить число баллов до 70%, 65%...). Олимпиада- это соревнование, а в любом соревновании бывают победители, они должны быть и здесь.)
II место присуждается участникам, набравшим от 50% до 75% от максимального числа баллов.
III место присуждается набравшим от 33 до 50%.
Олимпиадные задания по математике
2020год
7 класс
Задание 1. (7 баллов).
Поставьте вместо звездочек в выражение * + ** + *** + **** = 3330 десять различных цифр так, чтобы получилось верное равенство.
Задание 2.(7 баллов)
Решите уравнение: |5x|*|-1,5|=12
Задача 3(7 баллов)
Лифт едет с 1-го на 6-й этаж 15 секунд. За сколько секунд он проедет со 2-го по 10-й этаж?
Задание 4. (7 баллов).
В магазине картофель расфасовали в 24 пакета по 3 кг и 5 кг. Масса всех 5-килограммовых пакетов равна общей массе 3-килограммовых. Сколько было 3- и 5-килограммовых пакетов?
Задание5.(7 баллов)
На доске написано число 49. За один ход разрешается либо удваивать число, либо стирать его последнюю цифру. Можно ли за несколько ходов получить число 50?
Задание 6. (7 баллов).
Все внутренние углы выпуклого шестиугольника равны.
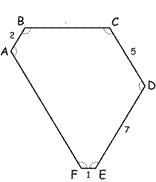 Длина некоторых сторон
указана на рисунке.
Длина некоторых сторон
указана на рисунке.
Найдите длину сторон AF и BC.
Задание 7.
Бригада косарей в первый день скосили половину луга и еще 2 га, а во второй день 25% оставшейся части и последние 6 га. Найти площадь луга.
Ответы и решения.
1. Например, 5 + 40 + 367 + 2918 = 3330.
2. Х= -1,6; Х=1,6
3. Решение. С 1-го по 6-й этаж – 5 этажей, 15:5=3(с) – лифт проезжает 1 этаж за 3 секунды. Со 2-го по 10-й будет 8 этажей, поэтому нужно затратить времени 3с · 8 = 24 с.
4. Так как масса 5-килограммовых пакетов равна массе 3- килограммовых пакетов, то наименьшее количество 5- килограммовых пакетов 3, а 3-кг пакетов – 5, т.е. 5*3=3*5, но тогда всего пакетов 3+5=8, в три раза меньше чем у нас есть, значит, пакетов по 5кг не 3, а 9, а по 3 кг – не 5, а 15.
Ответ: было 15 пакетов по 3 кг и 9 пакетов по 5 кг.
5. Ответ. Можно. Решение. Число 50 можно получить, удвоив 25, а 25 можно получить, стерев последнюю цифру числа 256, которое является степенью двойки. Таким образом, необходимая цепочка преобразований может выглядеть так: 49 → 4 → 8 → 16 → 32 → 64 → 128 → 256 → 25 → 50. Существуют и другие решения.
6. 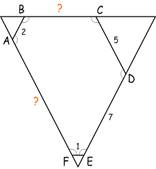 Исходный
шестиугольник достроим до треугольника. Так как сумма всех углов шестиугольника
равна 720° и все углы равны, то каждый угол равен 120°. Соответственно, смежные
с ними углы равны 60°. Построенный треугольник равносторонний. Приравняв его
стороны легко найти неизвестные отрезки AF и BC.
Исходный
шестиугольник достроим до треугольника. Так как сумма всех углов шестиугольника
равна 720° и все углы равны, то каждый угол равен 120°. Соответственно, смежные
с ними углы равны 60°. Построенный треугольник равносторонний. Приравняв его
стороны легко найти неизвестные отрезки AF и BC.
Ответ: AF=10, ВС=6
7. 6 га составляют 75% (3/4)
оставшейся части, значит, вся
оставшаяся часть равна 8 га. По
условию половина луга больше 8 га
на 2 га, т. е. равна 10 га ( 8 + 2 =10). Значит, весь луг занимал 20 га (10*2 = 20).
Ответ: 20 га.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.