Олимпиада

Муниципальный этап всероссийской олимпиады школьников по математике. 2020–21 учебный год

5 класс

Время выполнения заданий — 180 минут                             Максимальный балл — 100

В каждой из предложенных вам задач нужно написать правильный ответ. Ответ может быть числовой, а может быть строкой текста. Если в задаче требуется привести пример, достаточно указать один пример. Никаких решений задач писать не нужно! Условия задач можно оставить себе. Пользоваться калькулятором НЕ разрешается. Правильные ответы будут выложены на сайте www.kazan-math.info после олимпиады.

Задача 1. Расставьте в некоторых (можно во всех) промежутках между цифрами: 1 6 1 1 2 0 2 0 знаки арифметических действий («+», «−», «×», «÷») так, чтобы значение получившегося выражения равнялось 68. Можно использовать скобки.

Задача 2. Яна сложила три последовательных числа и получила сумму 39. Артем тоже нашел сумму трех последовательных чисел, но у него получилось 45. На сколько отличается наибольшее число Артема от наибольшего числа Яны?

Задача 3. Катя хочет подарить своим подружкам подарки. Если она купит каждой своей подруге по заколке за 28 рублей, то у нее останется 29 рублей. А если же купит каждой по браслету за 42 рубля, то ей не хватит 13 рублей. а) Сколько у Кати подруг?

б) Сколько у Кати денег на подарки?

Ответ оформить в виде «а) 100, б) 200».

Задача 4. Три каштана весят 50 граммов. Сколько каштанов на весах, если они показывают 3 кг?

Задача 5. Марья Ивановна пошла в кино с 5А, 5Б и 5В классами. Всего пошло 84 школьника. Билет стоил 50 рублей, но каждый 12-й школьник получал билет за полцены, а каждый 35-й школьник проходил бесплатно. Сколько всего денег заплатила Марья Ивановна за школьников?

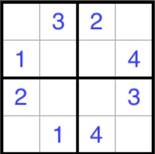Задача 6. В пустые ячейки квадрата 4×4 нужно вписать числа от 1 до 4 так, чтобы в каждом горизонтальном ряду, в каждой вертикальной колонке и в каждом из четырех выделенных квадратов 2×2 каждое число встречалось ровно по одному разу. Некоторые числа уже расставлены. В ответ нужно записать сумму четырех чисел, стоящих на диагонали, идущей из левого нижнего угла в правый верхний.

Задача 7. В корзинке лежат 9 желтых, 2 красных и 7 зеленых яблок. Какое наименьшее количество яблок нужно достать из корзинки, чтобы среди них обязательно нашлись яблоки всех трех цветов?

Задача 8. На числовой прямой обозначены точки. Какая координата у точки A?

Задача 9. Ваня записал на доске все натуральные числа от 1 до 100 включительно. Сколько четных цифр ему пришлось написать? (Цифра 0 — четная.)

Задача 10. В очереди в школьную столовую стоят пять мальчиков — Кирилл, Амир, Рома, Егор и Матвей. Кирилл стоит впереди Амира, но позади Матвея. Рома и Матвей не стоят рядом, а Егор не стоит рядом ни с Матвеем, ни с Кириллом, ни с Ромой. Кто из мальчиков стоит в середине очереди?

Задача 11. Тройняшки (они родились в один день) только что отметили свой третий день рождения. Через пять лет сумма их возрастов будет равна нынешнему возрасту их матери. Сколько лет будет их матери через пять лет?

Задача 12. Найдите наименьшее положительное целое число, которое заканчивается числом 17, делится на 17, а сумма его цифр тоже равна 17.

Задача 13. Пять детей нарисовали вместе 55 картин, но никто не нарисовал больше 13 картин. Какое наименьшее количество картин мог нарисовать один ребенок?

Задача 14. Найдите площадь закрашенной части, если площадь одного квадратика равна 1 см². Ответ дайте в квадратных сантиметрах.

Задача 15. Трое богатырей отправились к многоглавому дракону. Первый богатырь левой рукой отрубил половину всех голов, а правой — еще две. Второй богатырь тоже левой

рукой отрубил половину всех оставшихся голов, а правой — еще две. Затем третий богатырь сделал то же самое с оставшимися головами. После этого дракон упал на землю без голов. Сколько голов было у дракона в начале?

Задача 16. За мороженым в очереди стоят 29 детей. Катя стоит между Айдаром и Мишей (стоят именно подряд, между ними никого нет). Позади Айдара стоит вдвое больше детей, чем перед Мишей. Кто из мальчиков стоит перед Катей?

Задача 17. Назовем число «особенным», если сумма его цифр равна 11 и в записи числа нет цифры 0. Найдите разницу между наибольшим и наименьшим «особенными» числами.

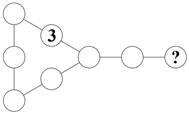Задача 18. Петя расставил в свободные кружочки на рисунке числа 2, 4, 6, 8, 12, 14 и 21 (каждое — по одному разу) так, чтобы произведение трех чисел на каждой из четырех прямых линий было одно и то же. Какое число могло оказаться на месте знака вопроса? Укажите все варианты.

Задача 19. Теперь учительница Марья Ивановна пошла с 5А классом в зоопарк. Она купила билеты своим ученикам и себе. Билет для взрослого был дороже, чем для школьника, но меньше, чем в два раза. Марья Ивановна заплатила 994 рубля. У Игоря Петровича в 5В было на троих учеников больше, чем у Марьи Ивановны, поэтому он заплатил 1120 рублей за своих учеников и себя. Сколько учеников было с Игорем Петровичем?

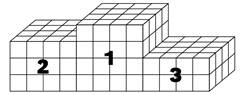
Задача 20. Для школьной олимпиады ученики 5Б построили подиум из деревянных кубиков (см. рисунок). Сколько всего кубиков они использовали? Дырок внутри подиума нет.