Муниципальный этап всероссийской олимпиады школьников по математике.   2020-21 учебный год

6 класс

Время выполнения заданий — 180 минут                                   Максимальный балл – 100 

В каждой из предложенных вам задач нужно написать правильный ответ. Ответ может быть числовой, а может быть строкой текста. Если в задаче требуется привести пример, достаточно указать один пример. Никаких решений задач писать не нужно! Условия задач можно оставить себе. Правильные ответы будут выложены на сайте www.kazanmath.info после олимпиады.

Задача 1.   Расставьте в ряд числа 1, 2, 3, 4, 5, 6, 7, 8  так, чтобы сумма первых пяти чисел равнялась 18, а сумма последних пяти чисел равнялась 27.

Задача 2.  На футбольный матч пришло некоторое количество зрителей. На следующий матч через неделю по рекомендации Роспотребнадзора было продано вдвое меньше билетов. А еще через неделю на третий матч было продано вдвое меньше билетов, чем на второй. Всего за три матча на стадионе было 14000 зрителей. Сколько зрителей было на втором матче? 

Задача 3. Айрат нарисовал окружность и треугольник. Получилась фигура, состоящая из трех частей (см. рисунок). Потом он нарисовал на другом листе окружность и прямоугольник. Какое наибольшее количество частей может оказаться во второй фигуре? 

Задача 4. Среднее арифметическое чисел 3, 5, 7, x и y равно 15. Чему равно среднее арифметическое чисел x и y?

Задача 5.  Грани куба покрашены в 6 цветов — А, Б, В, Г, Д и Е. На картинке показаны изображения куба с трех разных точек. Грань какого цвета находится напротив грани Д?

Задача 6. В бочке находится 30 литров смеси, содержащей 25% красных чернил, 30% желтых чернил и 45% воды. В бочку долили 5 литров желтых чернил. Какой процент от общего объема теперь занимают желтые чернила? 

Задача 7.  Фигуру с дыркой на картинке разрезали по клеточкам на

фигурки вида  (необязательно оба вида фигурок должны присутствовать). Какое а) наибольшее; б) наименьшее количество фигурок вида   могло оказаться? Ответ оформить в виде «а) 100, б) 200».

Задача 8.  Вычислить  (1,356+1,2∙1,37):(2,724+1,17∙2,8).

Задача 9. Расставьте в некоторых (можно во всех) промежутках между цифрами: 1 6 1 1 2 0 2 0 знаки арифметических действий («+», «–», «×», «÷») так, чтобы значение получившегося выражения равнялось 67. Можно использовать скобки. 

Задача 10. Придумайте какое-нибудь трехзначное число, в записи которого нет нулей, такое, что если к нему прибавить произведение всех его цифр, то получится число с таким же произведением цифр.

Задача 11. Найдите площадь закрашенной фигуры (см. рисунок). Площадь одной клетки равна 1.

Задача 12. Натуральные числа a и b таковы, что 20a+19b=365. Чему может равняться число 20b+19a? Укажите все возможные ответы.

Задача 13. Чему равно значение выражения  1+2–3+4+5–6+7+8–9+…+58+59–60 (после каждых двух операций сложения идет одно вычитание)?

Задача 14.  В пустые ячейки квадрата 4×4 нужно вписать числа от 1 до 4 так, чтобы в каждом горизонтальном ряду, в каждой вертикальной колонке и в каждом из четырех выделенных квадратов 2×2 каждое число встречалось ровно по одному разу. Некоторые числа уже расставлены. В ответ нужно записать сумму четырех чисел, стоящих на диагонали, идущей из левого нижнего угла в правый верхний.  

Задача 15. Сколько целых чисел от 1 до 999 содержат в своей записи ровно одну цифру 0? Задача 16. Четыре человека, каждый из которых либо рыцарь (говорит только правду), либо лжец (всегда лжет), высказали следующие утверждения. Первый: «Среди второго и третьего ровно один рыцарь». Второй: «Среди третьего и четвертого ровно один рыцарь». Третий: «Среди четвертого и первого ровно один рыцарь». Четвертый: «Первый и второй — оба рыцари». Известно, что не все четверо — лжецы. Кто из них рыцари? Укажите всех.

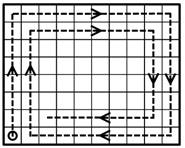Задача 17. Жук ползает по клеткам прямоугольника размером 40×60 (40 строк и 60 столбцов). Он начинает в левом нижнем углу, ползет вверх до упора, потом поворачивает направо, ползет вправо до упора, и так далее. При этом, когда он доходит до клетки, в которой уже побывал, он не идет в нее, а поворачивает направо. На рисунке изображено начала его маршрута. Когда ему некуда будет ползти, жук останавливается. В какой клетке он остановится? В ответе напишите а) номер ее строки, считая снизу вверх; б) номер ее столбца, считая слева направо. Ответ оформить в виде «а) 100, б) 200».

Задача 18. Сколько существует шестизначных чисел, которые начинаются на 20, заканчиваются на 20 и делятся на 18? 

Задача 19. Старший садовник стрижет один куст за 50 минут, первый помощник — за 1 час 15 минут, а второй помощник — за 1 час 20 минут. Сколько кустов они подстригут, работая вместе 4 часа? Они могут помогать друг другу и стричь куст вместе.

Задача 20. Из пункта A в пункт B выехал велосипедист. Одновременно с ним из пункта B в пункт A вышел пешеход, скорость которого в 5 раз меньше скорости велосипедиста. Когда они встретились, велосипедист продолжил путь в пункт B,  а пешеход развернулся и тоже пошел обратно в пункт B. Велосипедист же, доехав до пункта B, сразу же развернулся и поехал обратно в пункт A. В результате велосипедист вернулся в пункт A через 10 минут после того, как пешеход вернулся в пункт B. Сколько времени занял бы у пешехода путь из B в A?

Скорости пешехода и велосипедиста постоянны.