Олимпиада по информатике

Задача 1. Турнир

В турнире по круговой системе участвуют пять команд. Каждая команда должна сыграть один матч со всеми остальными командами.  Турнир  проводится в несколько туров, в каждом туре может быть сыгран один или несколько матчей. Разумеется, в одном туре каждая команда может сыграть не более одного матча.

Составьте расписание турнира, содержащее как можно меньше туров.

Ответ на эту задачу нужно записать в виде нескольких строк, каждая строка соответствует одному туру. Команды пронумерованы числами от 1 до 5. В каждой строке нужно перечислить через пробел игры, которые будут сыграны в этом туре. Каждая игра записывается в виде двух номеров команд, которые играют игру между собой в этом туре, слитно. Например, запись в одной строке «12 34» обозначает, что в этом туре играют команды номер 1 и 2 в одном матче и команды номер 3 и 4 в другом матче.

Порядок записи команд в матче и порядок записи матчей в одном туре не важен.

Чем меньше туров будет в составленном вами расписании, тем больше баллов вы получите, при условии корректности составленного расписания (все команды сыграли друг с другом ровно по одному матчу, каждая команда в каждом туре играет не более одного раза).

Решение

Можно составить турнир, содержащий пять туров. Пример такого турнира.

12 34

13 25

15 24

14 35

23 45

Возможны и другие ответы.

Задача 2. Дорожка в парке

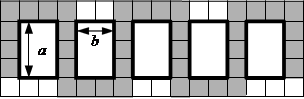На приведённом рисунке изображено n = 5 клумб размерами a = 3 и b = 2 метра. Клумбы изображены большими белыми прямоугольниками, дорожка закрашена серым цветом. Сторона одной клетки – 1 метр. В данном примере площадь дорожки равна 38 м2. Обратите внимание на концы дорожек.

Ответом на эту задачу является некоторое выражение, которое может содержать целые числа, переменные a, b и n (записываемые английскими буквами), операции сложения (обозначается «+»), вычитания (обозначается «−»), умножения (обозначается «*») и круглые скобки для изменения порядка действий. Запись вида «2a» для обозначения произведения

числа 2 и переменной a неверная, нужно писать «2 * a».

Пример правильного (по форме записи) выражения: a * n + (b − a) * 2.

Решение

Количество клеток в верхней и нижней строке равно (b + 2) * n. Количество клеток в остальных рядах равно a * (n + 1). Итоговый ответ.

(b + 2) * n + a * (n + 1)

Задача 3. Расстановка знаков

Легенда гласит, что Карл Фридрих Гаусс, учась в школе, смог быстро посчитать сумму всех целых чисел от 1 до 100, заметив, что 1 + 100 = 2 + 99 = … = 50 + 51 = 101.

Поэтому сумма всех целых чисел от 1 до 100 равна 101 × 50 = 5050.

Теперь решите задачу посложнее: как расставить перед каждым из чисел от 1 до N знаки «+» или «−» так, чтобы сумма получившихся чисел была равна 0? Например, для N = 3 сумма −1 −2 +3 будет равна 0.

Решите эту задачу для четырёх значений N: N = 8, N = 15, N = 40, N = 99.

Ответ на эту задачу нужно записать в виде 4 строк. Каждая строка должна содержать только  знаки  «+» и «−». В первой строке должно быть  8 знаков,  во второй строке – 15,        в третьей – 40, в четвертой – 99. Последовательность знаков в каждой строке соответствует последовательности знаков, которые нужно расставить перед числами 1, 2, …, N так, чтобы сумма была равна 0. Например, для N = 3 ответ нужно записать в виде «++−» или «−−+».

Если вы не можете решить задачу для какого-то значения N, то поставьте в этой строке один знак «+». Решение будет принято на проверку, если оно содержит четыре строки, каждая из  которых  состоит  из  символов  «+»  или  «−».  Количество  символов  в  строках  и правильность ответа сразу после сдачи не проверяется.

Решение

Возможный правильный ответ (ответ на четвёртый вопрос ниже занимает две строки, но при сдаче ответа должен быть записан в одной строке):

+--++--+

++-+--++--++--+

+--++--++--++--++--++--++--++--++--++--+

++-+--++--++--++--++--++--++--++--++--++--++--++--++--++--++--++--

++--++--++--++--++--++--++--++--+

Пояснение. Сумма +1−2−3+4 равна 0. Аналогично, перед 4 любыми идущими подряд числами можно расставить знаки «+−−+», и сумма будет равно 0. Поэтому в ответе на первый вопрос (N = 8) строку «+−−+» нужно повторит 2 раза, а в ответе на третий вопрос (N = 40) строку «+−−+» нужно повторит 10 раз.

Для ответом на второй и четвёртый вопрос заметим, что числа 15 и 99 дают остаток 4 при делении на 4. А перед числами 1, 2, 3 можно расставить знаки «+» и «−» требуемым образом: «++−» или  «−−+». Поэтому для   N = 15 ответ можно  составить  из строки «++−»,   и следующей за ней строкой «+−−+», повторённой 3 раза. Для N = 99 ответ можно составить из строки «++−», и следующей за ней строкой «+−−+», повторённой 24 раза.

Допускаются и другие правильные ответы.

Задача 4. Решение задач

Учитель математики выдал Маше листок с хитрым заданием: на листке было двенадцать задач, но в условиях некоторых из них были пропуски и заполнить их можно было, только решив некоторые другие задачи. К листку прилагалось пояснение.

·         Для решения задачи Н необходимо решить задачи K и F.

·         Решив задачу A, вы сможете решить задачи I и K.

·         Задача C не решается без задачи B, которая, в свою очередь, не решается без задачи D.

·         Задачу F можно решить, предварительно решив задачу J, а также любую из задач D

или I.

·         Для решения задачи L необходимо решить или задачу G, или задачу H.

·         Если решить задачу C, а также хотя бы одну из задач A или D, то можно решить задачу E.

Посмотрев на задачи, Маша составила табличку, в которой записала время в минутах, необходимое ей для решения каждой задачи:

Ответьте на вопросы.

1.              (1 балл) С какой задачи Маша может начать решать эти задачи? Перечислите все возможные варианты выбора первой задачи.

2.              (2 балла) В какой последовательности Маша должна решать задачи, если она хочет решить их все? Напишите любую правильную последовательность решения задач.

3.              (3 балла) Маша очень хочет решить задачу E, так как она самая интересная. В какой последовательности нужно решать задачи, чтобы как можно быстрее добраться до неё? Нужно решить не все задачи, время, потраченное на решённые задачи, должно быть как можно меньше.

4.              (4 балла) Как должна действовать Маша, если она хочет решить как можно больше задач за 45 минут?

Ответ на эту задачу нужно записать в четырёх строках, каждая строка должна содержать ответ на один соответствующий вопрос. В каждой строке должны быть указаны какие-то из букв A–L, без разделителей, буквы не должны повторяться в одной строке.

В первом вопросе порядок записи букв не важен. В остальных вопросах нужно записать буквы в той последовательности, в которой будут решаться задачи.

Во втором вопросе в ответе должны быть указаны все буквы от A до L в порядке решения задач.

В третьем вопросе последовательность решённых задач должна заканчиваться буквой Е. Чем меньше времени будет потрачено на решение данной последовательности задач, тем больше баллов вы получите.

В четвёртом вопросе нужно привести пример решения последовательности задач, занимающей не более 45 минут. Чем больше задач будет в приведённой последовательности, тем больше баллов вы получите.

Решение будет принято на проверку, если оно содержит четыре строки, каждая строка содержит только возможно допустимые буквы, буквы в строках не повторяются. Если вы не можете дать ответ на какой-нибудь вопрос, напишите в этой строке какую-нибудь одну букву.

Решение

Возможные ответы на задание.

ADGJ ADBCEGIJFKHL DBCE

ADBCEJF

В первом задании допускается любая перестановка символов A, D, G, J. Во втором задании допустимы и другие ответы.

В третьем задании это единственный верный ответ.

В четвёртом задании есть и другие ответы, наилучший ответ содержит 7 задач.

Задания по программированию

Решения задач 5–7 совпадают с решениями задач 1–3 для 9–11 классов.

Скачано с www.znanio.ru