Олимпиады 8 класс

Задания олимпиады 8 класс

1. Найдите какие-нибудь четыре различных натуральных числа, обладающих следующим свойством: если к произведению любых двух из них прибавить произведение двух остальных чисел, то получится простое число.

2. В выпуклом четырехугольнике ABCD точка K — середина AB,

точка L — середина BC, точка M — середина CD, точка N — середина DA. Для некоторой точки S, лежащей внутри четырехугольника ABCD, оказалось, что KS = LS и NS = MS. Докажите, что ∠KSN = ∠MSL.

3. Рабочие укладывали пол размера n × n плитками двух типов: 2 × 2 и 3 × 1. Оказалось, что им удалось полностью уложить пол так, что было использовано одинаковое количества плиток каждого типа. При каких n такое могло получиться? (Резать плитки, а также накладывать их друг на друга нельзя.)

4. Сумма чисел a, b и c равна нулю, а их произведение отрицательно. Докажите, что число  положительно.

5. На столе лежат 300 монет. Петя, Вася и Толя играют в следующую игру. Они ходят по очереди в следующем порядке: Петя, Вася, Толя, Петя, Вася, Толя, и т. д. За один ход Петя может взять со стола 1, 2, 3 или 4 монеты, Вася — 1 или 2 монеты, а Толя — тоже 1 или 2 монеты. Могут ли Вася и Толя договориться так, что, как бы ни играл Петя, кто-то из них двоих заберет со стола последнюю монету?

Ключ

1.     Найдите какие-нибудь четыре различных натуральных числа, обладающих следующим свойством: если к произведению любых двух из них прибавить произведение двух остальных чисел, то получится простое число.

Решение.

Подойдут, например, числа 1, 2, 3 и 5. Действительно, значения всех трех выражений 1 · 2 + 3 · 5 = 17, 1 · 3 + 2 · 5 = 13 и 1 · 5 + 2 · 3 = 11 являются простыми числами.

Замечание.

 Существуют и другие примеры, такие, как (1, 2, 3, 13), (2, 5, 11, 17) или (4, 5, 7, 11). Нетрудно понять, что в любом таком примере должно быть ровно одно чётное число.

2.     В выпуклом четырехугольнике ABCD точка K — середина AB, точка L — середина BC, точка M — середина CD, точка N — середина DA. Для некоторой точки S, лежащей внутри четырехугольника ABCD, оказалось, что KS = LS и NS = MS. Докажите, что ∠KSN = ∠MSL.

Решение.

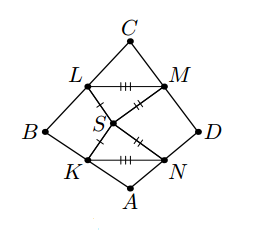
Заметим, что отрезок KN является средней линией треугольника BAD. Значит, KN = BD 2 . Аналогично, из треугольника BCD получаем

 LM = BD 2 . Но тогда треугольники KSN и MSL равны по трем сторонам. Отсюда следует требуемое равенство соответствующих углов.

Замечание. Из условия следует, что диагонали четырехугольника ABCD перпендикулярны.

3.     Рабочие укладывали пол размера n × n плитками двух типов: 2 × 2 и

3 × 1. Оказалось, что им удалось полностью уложить пол так, что было использовано одинаковое количества плиток каждого типа. При каких n такое могло получиться? (Резать плитки, а также накладывать их друг на друга нельзя.)

Ответ. При n, делящихся на 7.

Решение.

Пусть рабочие использовали по x плиток каждого вида. Тогда площадь, занятая плитками, равна 4x + 3x = 7x = n ² . Значит, n должно делиться на 7.

Если же n делится на 7, то пол уложить можно. Достаточно заметить, что квадрат 7×7 можно уложить, используя по 7 плиток каждого вида. А квадрат 7k ×7k можно разрезать на квадраты 7 × 7.

4.      Сумма чисел a, b и c равна нулю, а их произведение отрицательно. Докажите, что число  положительно.

Решение.

Так как abc < 0, то либо одно из чисел a, b, c отрицательно, либо все три. Но a + b + c = 0, поэтому все три числа отрицательными быть не могут.

Пусть, без ограничения общности, a > 0, b > 0 и c < 0. Нам нужно доказать, что  > 0.

Или  

Так как a > 0 и b > 0, то .

Аналогично .

Сложив два полученных неравенства, получим требуемое.

Замечание.

Можно заметить, что, если c отрицательно, а a и b положительны, то

|c| = a+b > a.

Поэтому

кроме того   .

5.     На столе лежат 300 монет. Петя, Вася и Толя играют в следующую игру. Они ходят по очереди в следующем порядке: Петя, Вася, Толя, Петя, Вася, Толя, и т. д. За один ход Петя может взять со стола 1, 2, 3 или 4 монеты, Вася — 1 или 2 монеты, а Толя — тоже 1 или 2 монеты. Могут ли Вася и Толя договориться так, что, как бы ни играл Петя,

кто-то из них двоих заберет со стола последнюю монету?

Ответ. Не могут.

Решение. Покажем, как играть Пете, чтобы он смог забрать со стола последнюю монету независимо от игры Васи и Толи. Пусть первым ходом Петя возьмет 4 монеты. Заметим, что Вася и Толя за свои ходы суммарно могут взять от 2 до 4 монет. Это значит, что после первого хода Толи на столе останется от 292 до 294 монет. После этого Пете нужно взять 2, 3 или 4 монеты так, чтобы на столе осталось 290 монет. А теперь, если Вася и Толя будут брать суммарно 2, 3 или 4 монеты, Пете нужно брать соответственно 3, 2 или 1 монету, чтобы после каждого его хода число монет, остающихся на столе, делилось на 5. Таким образом, он оставит 285, 280, . . . , 5 и, наконец, 0 монет, то есть заберет со стола последнюю монету.

Замечание. Существуют и другие выигрышные стратегии Пети.