Практическая работа №2

Тема: Операции над числами в естественной и нормальной формах

Цель:

 - закрепление знаний о способах выполнения арифметических операций в двоичной, восьмеричной и шестнадцатеричной системах счисления;

 - формирование практических навыков по выполнению арифметических операций в различных системах счисления.

Время выполнения: 2 часа.

Теоретические сведения

Арифметические операции во всех позиционных системах счисления выполняются по одним и тем же правилам.

Сложение. Рассмотрим сложение в двоичной системе счисления. В его основе лежит таблица сложения одноразрядных двоичных чисел:

0+0=0

0+1=1

1+0=1

1+1=10

При сложении двух единиц происходит перевыполнение разряда и производится перенос в старший разряд. Переполнение разряда наступает тогда, когда значение числа в нем становится равным или большим основания. Для двоичной системы счисления, это число равно двум. Сложение многоразрядных двоичных чисел происходит с учетом возможных переносов из младших разрядов в старшие.

Вычитание. Рассмотрим вычитание двоичных чисел. В его основе лежит таблица вычитания одноразрядных двоичных чисел. При вычитании из меньшего числа (0) большего (1) производится заем из старшего разряда. Вычитание многоразрядных двоичных чисел происходит в соответствии с таблицей вычитания с учетом возможных займов в старших разрядах.

0-0=0

0-1=10 (с займом)

1-0=1

1-1=0

Умножение. В основе умножения лежит таблица умножения одноразрядных двоичных чисел.

Деление. Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления.

Арифметические операции в восьмеричной и шестнадцатеричной системах счисления. Аналогично, можно выполнить арифметические действия в восьмеричной и шестнадцатеричной системах счисления. Необходимо только понять, что перенос в следующий разряд при сложении и заем из старшего разряда при вычитании определяется величиной основания системы счисления. Для проведения арифметических операций над числами, представленными в различных системах счисления, необходимо предварительно перевести их в одну систему.

Пример 1. Сложим двоичные числа 110₂ и 11₂. При сложении двух единиц происходит переполнение разряда и производится перенос в старший разряд. Переполнение разряда наступает тогда, когда значение числа в нем становится равным или больше основания. Для двоичной системы счисления, это число равно двум.

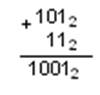
Пример 2. В качестве примера произведем вычитание двоичных чисел 110₂ и 11₂. При Вычитании из меньшего числа (0) большего (1) производится заем из старшего разряда.

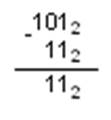
Пример 3. При выполнении арифметических действий в других системах счисления необходимо помнить, что перенос в следующий разряд при сложении при сложении и заем из старшего разряда при вычитании определяется величиной основания системы счисления. Вычитание многоразрядных двоичных чисел происходит с учетом возможных займов старших разрядах. Сложение многоразрядных двоичных чисел происходит с учетом возможных переносов из младших разрядов в старшие.

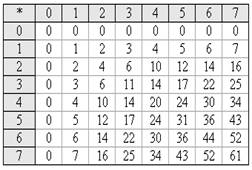
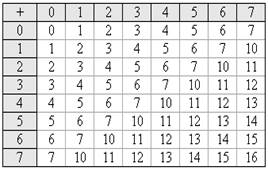
Умножение в восьмеричной                            Сложение в восьмеричной

системе счисления                                                  системе счисления

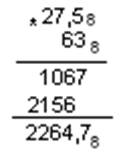
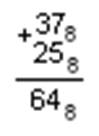
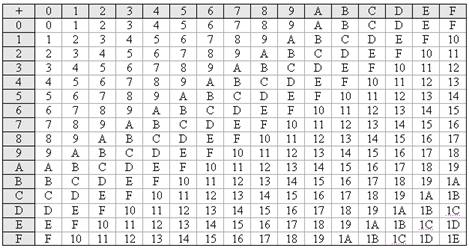
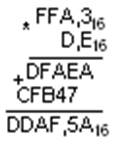
Сложение в шестнадцатеричной системе счисления

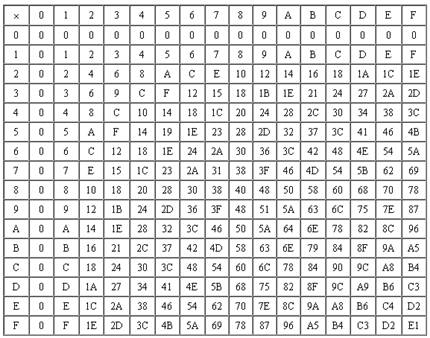
Умножение в шестнадцатеричной системе счисления

Пример 4. Выполните умножение двоичных чисел 110₂ и 11₂. Умножение многоразрядных двоичных чисел происходит по обычной схеме, применяемой в десятичной системе счисления с последовательным умножением множимого на очередную цифру множителя.

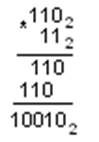
Пример 5. Выполните деление двоичных чисел 101000101₂ и 1101_2. Для деления в двоичной системе счисления нужно уметь сравнивать числа (определять, какое больше) и хорошо вычитать.

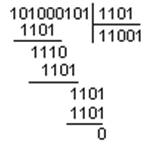
Пример 6. Выполните деление двоичных чисел 1001₂ и 11₂ с точностью до 3 знаков после запятой.

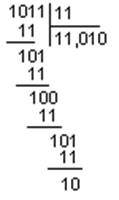
Задания к практической работе

Задание 1. Сложите числа:

1)      а)11111001101₂+1111111₂                  б) 56037₈+55572₈;

2)      а)101010111₂+111110₂                                       б) 5BE1₁₆+70EF3₁₆;

3)      а)1111101₂+1010011₂                         б) 536₈+5673₈;

4)      а)111₂+101011₂                                                          б) EB5₁₆+7CB₁₆;

5)      а) 110111+1110                                  б) 1FC₁₆ + 1D1₁₆;

6)      а) 110111+10111                                б) AB₁₆ + EF₁₆;

7)      а) 1111001+1011101                          б) 165₈ + 37₈;

8)      а) 1110001+10001                              б) F9E₁₆ + 2А30₁₆.

Задание 2. Выполните вычитание:

1)      а) 10100₂ - 111₂                                                          б) 20₈ - 15₈;

2)      а) 1011₂ - 1001₂                                   б) 567₈ – 201₈;

3)      а) 10010₂ – 1111₂                                б) ABC₁₆ – 5678₁₆;

4)      а) 111011₂ – 10001₂                           б) 2A30₁₆ – F9E₁₆;

5)      а) 10101₂ - 11₂                                    б) 7631₈ – 456₈;

6)      а) 101111101101₂ - 01111001₂            б) BEDA₁₆ – ВАС₁₆;

7)      а) 111111101010₂ – 01110101₂           б) 7325₈ – 346₈;

8)      а) 11110101₂ – 101011₂                      б) FA9C₁₆ – B7A₁₆.

Задание 3. Выполните умножение:

1)      а) 100111₂* 1000111₂                                           б) 1170₈ * 46₈;

2)      а) 61A₁₆ * 40D₁₆                                                         б) 100001₂*1001010₂;

3)      а) 172₈*15₈                                         б) 543₁₆*96₁₆;

4)      а) 1011010₂*1000010₂                                         б) 632₈*141₈;

5)      а) 2A7₁₆*188₁₆                                                             б) 1011100₂*1100100₂;

6)      а) 347₈*125₈                                                                  б) 10A₁₆*35₁₆;

7)      а) 1101100₂*1010011₂                                         б) 516₈*44₈;

8)      а) 618₁₆*48₁₆                                                                 б) 1000000₂*110110₂.

Задание 4. Выполните деление:

1)           а) 110011000₂:10001₂                         б) 2410₈:27₈;

2)           а) D4A₁₆:1B₁₆                                             б) 10010100100₂:1100₂;

3)           а) 2760₈:23₈;                             б) 4AC₁₆:17₁₆;

4)           а) 111010110₂:1010₂;                б) 4120₈:23₈;

5)           а) 4F8₁₆:18₁₆;                            б) 1000101000₂:1100₂;

6)           а) 5101₈:31₈                              б) D7A₁₆:1E₁₆;

7)           а) 11000100000₂:10000₂           б) 3074₈:25₈;

8)           а) 6D5₁₆:21₁₆                             б) 10001110011₂:10001₂.

Контрольные вопросы и здания:

1.     Дать определение системы счисления. Назвать и охарактеризовать свойства системы счисления.

2.     Что называется основанием системы счисления?

3.     Чему равны веса разрядов слева от точки, разделяющей целую и дробную часть, в двоичной системе счисления (восьмеричной, шестнадцатеричной)?

4.     Чему равны веса разрядов справа от точки, разделяющей целую и дробную часть, в двоичной системе счисления (восьмеричной, шестнадцатеричной)?

5.     Расскажите об алгоритме выполнения сложения в двоичной, восьмеричной и шестнадцатеричной системах счисления.

6.     Расскажите об алгоритме выполнения вычитания в двоичной, восьмеричной и шестнадцатеричной системах счисления.

7.     Переведите числа из десятичной системы счисления в другие (двоичную, восьмеричную и шестнадцатеричную) и выполнить арифметические операции (сложение, вычитание и умножение в указанных системах счисления): 247₁₀, 123₁₀.

Скачано с www.znanio.ru