ОПРЕДЕЛЕНИЕ ЧИСЛОВОГО НЕРАВЕНСТВА

Определение числового неравенства

Цели: повторить правила сравнения чисел; ввести определение понятия числового неравенства; формировать умение использовать данное определение для сравнения чисел и доказательства неравенств.

Ход урока

I. Организационный момент.

II. Анализ результатов контрольной работы.

1. Объявить результаты контрольной работы, выделить типичные ошибки, допущенные учащимися при её выполнении.

2. Вынести на доску решение заданий, с которыми учащиеся не справились.

III. Актуализация знаний.

Необходимо вспомнить с учащимися материал о сравнении действительных чисел. Напоминаем, что геометрически определению понятий «больше» и «меньше» соответствует взаимное расположение точек на координатной прямой: из двух чисел больше то, которое на координатной прямой расположено правее, и меньше то, которое расположено левее. Используя координатную прямую, учащимся следует помнить, что всякое отрицательное число меньше нуля. Затем повторяем правила сравнения чисел:

1. Всякое отрицательное число меньше любого положительного числа.

2. Из двух дробей с одинаковым знаменателем больше та, у которой больше числитель.

Отсюда следует, что для сравнения обыкновенных дробей, необходимо сперва привести их к общему знаменателю.

3. Из десятичных дробей больше та, у которой больше целая часть. Если целые части совпадают, то сравниваем в разрядах десятых, сотых, тысячных и т. д., пока не «увидим» большую цифру в разряде.

4. Чтобы сравнить обыкновенную и десятичную дроби, приведём обыкновенную дробь к десятичной и сравним две десятичные дроби.

5. Из двух отрицательных чисел больше то, модуль которого меньше.

IV. Устная работа.

1. Поставьте вместо * знак =, > или < так, чтобы получилось верное равенство или неравенство:

а) –15 * 0;                       б) 3 * 0;                            в)  * 2;

г)  * ;             д) 1,25 * 1;            е) 0,6 * ;

ж)  * ;                 з) –0,07 * ;                   и) –5,6786 * –5,679.

2. Сравните с нулём значение выражения:

а) (–6,3)³;         б) (–2,1)⁴;         в) 0⁵;         г) 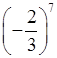;         д) .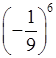

V. Объяснение нового материала.

1. После актуализации знаний возникает потребность в таком способе сравнения, который позволил бы охватить все рассмотренные числа. Удобнее и проще всего проводить сравнение числа с нулём, поэтому вводится следующее  о п р е д е л е н и е:  число а больше числа b, если разность а – b – положительное число; число а меньше числа b, если разность а – b – отрицательное число.

Замечаем, что если разность а – b равна нулю, то числа а и b равны.

2. Рассматриваем рис. 22 на с. 153 ученика и получаем геометрическую интерпретацию нового определения.

3. Разбираем пример № 1 на с. 153 учебника. Можно предложить учащимся составить другую разность – между правой и левой частями неравенства. После преобразования получится положительное число. Просим учащихся сделать соответствующий вывод.

VI. Формирование умений и навыков.

Все  у п р а ж н е н и я,  решаемые  на  этом  уроке,  можно  разделить на  д в е   г р у п п ы:

1) на непосредственное применение определения числового неравенства (сравнение чисел);

2) на доказательство числовых неравенств (определение верности неравенства при любом значении, входящей в его запись буквы).

1. № 724, № 725 (устно).

2. № 726.

Р е ш е н и е

При а = –5

3а(а + 6) = 3 · (–5) (–5 + 6) = –15,

(3а + 6)(а + 4) = (3 ·(–5) + 6)(–5 + 4) = –9;

значит, 3а(а + 6) < (3а + 6)(а + 4).

При а = 0

3а (а + 6) = 3 · 0 (0 + 6) = 0,

(3а + 6) (а + 4) = (3 · 0 + 6) (0 + 4) = 24;

значит, 3а(а + 6) < (3а + 6)(а + 4).

При а = 40

3а (а + 6) = 3 · 40 (40 + 6) = 5520,

(3а + 6) (а + 4) = (3 · 40 + 6) (40 + 4) = 5544;

значит, 3а(а + 6) < (3а + 6)(а + 4).

Докажем, что 3а(а + 6) < (3а + 6)(а + 4) при любом значении а. Составим разность выражений:

3а(а + 6) – (3а + 6)(а + 4) = 3а² + 18а – 3а² – 12а – 6а – 24 = –24.

При  любом а рассматриваемая  разность  отрицательна,  значит, 3а(а +
+ 6) < (3а + 6)(а + 4).

3. № 728 (а, б), № 729 (а, г), № 730 (а, в).

Р е ш е н и е

№ 728.

а) 3(а + 1) + а – 4(2 + а) = 3а + 3 + а – 8 – 4а = –5 < 0, значит, неравенство верно при любом значении а.

б) (7p – 1)(7p + 1) – 49² = 49p² – 1 – 49p² = –1 < 0, значит, неравенство верно при любом значении р.

№ 729.

а) 2b² – 6b + 1 – 2b(b – 3) = 2b² – 6b + 1 – 2b² + 6b = 1 > 0, значит, неравенство верно при любом значении b.

г) 8y(3y – 10) – (5y – 8)² = 24y² – 80y – 25y² + 80y – 64 = –y² – 64 = –(y² +
+ 64) < 0, значит, неравенство верно при любом значении у.

Надо обратить внимание учащихся, что если у² + 64 > 0 для любого у, то противоположное ему по значению выражение –(у² + 64) < 0.

№ 730.

а) 4x(x + 0,25) – (2x + 3)(2x – 3) = 4x² + x – 4x² + 9 = x + 9.

Выражение  может  быть  как  положительным,  так  и  отрицательным, а также  равным  нулю  в  зависимости  от  х,  значит,  неравенство  не  верно  при любых х.

в) (3x + 8)² – 3x(x + 16) = 9x² + 48x + 64 – 3x² – 48x = 6x² + 64 > 0, значит, неравенство верно при любом значении х.

4. № 732 (а, б).

Р е ш е н и е

а) 10а² – 5а + 1 – а² – а = 9а² – 6а + 1 = (3а – 1)² ≥ 0, значит, неравенство верно при любом значении а.

б) 50а² – 15а + 1 – а² + а = 49а² – 14а + 1 = (7а – 1)² ≥ 0, значит, неравенство верно при любом значении а.

VII. Итоги урока.

В о п р о с ы   у ч а щ и м с я:

– Сформулируйте правила сравнения положительных чисел, отрицательных, разного знака.

– Сформулируйте правила сравнения обыкновенных дробей, десятичных.

– Сформулируйте универсальный способ сравнения чисел. Приведите геометрическую интерпретацию.

Домашнее  задание:  № 727,  № 728 (в, г),  № 729 (б, в),  № 730 (б, г), № 745 (а).