Поделиться
ОПРЕДЕЛЕНИЕ СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ.docx
Определение степени с натуральным показателем
Цели: ввести понятие степени числа а с натуральным показателем п; определить значение степени с натуральным показателем положительного и отрицательного числа в зависимости от четности / нечетности показателя степени; формировать умение вычислять значение степени и представлять число в виде степени с натуральным показателем.
Ход урока
I. Организационный момент
Устная работа.
Вычислите.
а) 3 · 45; б) 
· 120; в)
;
г) 
; д) 
· 49; е)
–3 · (–16);
ж) –(–3) · 12; з) –(2 · (–9)); и)
;
к) 18 ·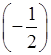 
+ 11; л) 
· (11
– 6); м)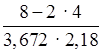 
.
II. Объяснение нового материала.
1. Объяснение проводить согласно пункту 18 учебника. Напоминаем, что вместо длинной записи произведения 5 · 5 · 5 · 5 · 5 · 5 · 5 можно записать выражение 57, где 5 – основание степени (повторяющийся множитель), а 7 – показатель степени (число повторяющихся множителей).
Понятие степени определяем для любого числа а в качестве основания и любого натурального показателя (аналитическая запись).
На доску выносится запись:
|
Степенью числа а с натуральным показателем п, большим 1, называется выражение ап, равное произведению п множителей, каждый из которых равен а. Степенью числа а с показателем 1 называется само число а. |
Проговариваем с учащимися правило чтения степени, приводим примеры.
2. Мини-лабораторная работа.
Найдите значение степени.
33; 34; 35; 36; 01;
; 02;
(0,1)2; (0,1)3; (0,1)4; (0,1)5; 03;
(–2)2; (–2)3; (–2)4; (–2)5; 04;
; 05;
(–0,1)2; (–0,1)3; (–0,1)4; (–0,1)5; 06.
Задания разбиваем либо по группам, либо раздаем индивидуально. Затем «по цепочке» ученики выходят к доске и записывают результаты.
После анализа полученных результатов на доску выносятся следующие правила:
|
При возведении в степень положительного числа получается положительное число. |
|
При возведении в степень нуля получается нуль. |
|
Степень отрицательного числа с четным показателем – положительное число. |
|
Степень отрицательного числа с нечетным показателем – отрицательное число. |
Обособленно выносим правило для квадратов чисел (пропедевтика изучения решения квадратных уравнений):
|
Квадрат любого числа есть положительное число либо нуль (а2 ≥ 0 при любом а). |
3. Рассматриваем примеры 1–3 со с. 88–89 учебника.
III. Формирование умений и навыков.
Упражнения, решаемые на этом уроке, можно условно разбить на группы:
1-я группа. Задания на усвоение понятия степени.
2-я группа. Задания на вычисление значения степени числа с натуральным показателем.
3-я группа. Задания на вычисление значения числового выражения, содержащего степень.
1-я группа
№ 374, № 375 (устно), № 376, № 378, № 380.
При выполнении этих заданий учащиеся должны четко называть степень, можно просить назвать их основание и показатель степени.
2-я группа
1. № 382, № 381 (а, б).
2. Не выполняя вычислений, сравните значение данного выражения с нулем:
а) (–4,1) · (–5,6)6; б) (–3,3)3 : (–5,7);
в) –(4,8)2 · (–1,2)4; г) –(–2,7)4 · (–6,4)5.
3. Сравните значения выражений:
а) (–6,5)4 и (–2,4)3;
б) (–0,2)6 и (–0,2)10;
в) (–1,5)7 и (–1,5)9.
3-я группа
№ 384, 385 (а, в, г), 386 (а, в, д, ж), 387 (а, б, в).
IV. Итоги урока.
– Сформулируйте определение степени числа с натуральным показателем. Приведите примеры и назовите в каждом из них основание и показатель степени.
– Чему равна первая степень любого числа?
– Какой знак имеет результат возведения положительного числа в натуральную степень?
– Какой знак имеет значение степени отрицательного числа с четным показателем? С нечетным показателем?
– Каков порядок действий при нахождении значения выражения, содержащего степени с натуральным показателем?
Домашнее задание: № 377; 379; 381 (в, г); 383; 385 (б, г, е); 386 (б, г, е, з).
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
