ОПРЕДЕЛЕНИЕ СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ

Определение степени с натуральным показателем

Цели:  продолжить  формировать  умение  вычислять  значение  числового  выражения,  содержащего  степень;  формировать  умение  вычислять значение буквенного выражения, содержащего степень, и решать практические задачи с использованием понятия степени с натуральным показателем.

Ход урока

I. Математический диктант.

Вариант 1

1. Запишите в виде произведения третью степень числа 4 и найдите её числовое значение.

2. Чему равна первая степень числа –5?

3. Вычислите значение выражения 2³ · 0,5.

4. Чему равна сумма кубов чисел 5 и 3?

5. Вычислите значение выражения (–3)² + (0,1)³.

Вариант 2

1. Запишите в виде произведения четвертую степень числа 3 и найдите её числовое значение.

2. Чему равна первая степень числа ?

3. Вычислите значение выражения 3² · 0,7.

4. Чему равен квадрат разности чисел 7 и 5?

5. вычислите значение выражения (–5)³ – (0,2)².

II. Актуализация знаний.

№ 387 (г, д, е, ж, з, и), № 388.

№ 388.

Решение:

а) –1³ + (–2)³ = –1 + (–8) = –9;

б) –6² – (–1)⁴ = –36 – 1 = –37;

в) –8³ + (–3)³ = –512 + (–27) = –539;

г) 10 – 5 · 2⁴ = 10 – 5 · 16 = 10 – 80 = –70;

д) 2 · 3⁴ – 3 · 2⁴ = 2 · 81 – 3 · 16 = 162 – 48 = 114;

е) 2 · 5³ + 5 · 2³ = 2 · 125 + 5 · 8 = 250 + 40 = 290;

ж) 3⁴ – 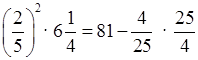 = 81 – 1 = 80;

з) 0,2 · 3² – 0,4 · 2⁴ = 0,2 · 3² – 0,2 · 2 · 2⁴ = 0,2(3² – 2 · 2⁴) =
= 0,2(9 – 2 · 16) = 0,2 · (9 – 32) = 0,2 · (–23) = –4,6;

и) 8 · 0,5³ + 25 · 0,2² = 2 ³ · 0,5³ + 5² · 0,2² = (2 · 0,5)³ + (5 · 0,2)² =
= 1³ + 1² = 1 + 1 = 2.

При выполнении этого упражнения учащиеся выводят правило:

III. Формирование умений и навыков.

На этом уроке отрабатывается умение вычислять значение буквенного выражения, содержащего степень.

1-й блок

1. Найдите значения выражений х²; – х²; х² – 4 для заданных значений х и заполните таблицу (используйте найденные значения выражения х² для вычисления значений двух других выражений):

2. Найдите значение выражений х³; 0,1х³; х³ + 10 для заданных значений х и заполните таблицу:

3. № 392 (устно).

2-й блок

1. Найдите значение выражения.

а) (ху)² при х = 12 и у = –0,5; х = –14 и у = –1;

б)  при х = –6 и у = 1,5; х = 0 и у = –23;

в) (х + у)⁴ при х = 0,7 и у = 0,3; х = –11 и у = 6;

г) (у – х)³ при х = –14 и у = –10; х = 0,9 и у = 1,1.

2. № 393.

3. Сравните значения выражений.

а) –а² и (–а)² при а = 3; –5; 0;

б) –а³ и (–а)³ при а = 10; –2; 0.

4. № 395.

Решение:

а) а³ · а = (а · а · а) · а = а⁴;

б) а⁴ · а² = (а · а · а · а) · (а · а) = а⁶;

в) а³ · а⁶ = 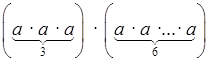 = а⁹;

г) а²⁰ · а¹² = 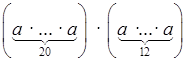 = а³².

№ 396, № 397.

3-й блок

1. № 389.

2. Сколько биений сделает сердце человека за сутки, если за 1 мин оно делает в среднем 75 биений?

3. Может  ли  школьник  поднять  1 м³  пробки?  (Масса  1 см³  пробки 0,2 г.)

Решение:

Рассчитаем, сколько см³ в 1 м³:

1 м³ = 1 · 1 · 1 ( в м) = 100 · 100 · 100 (в см) = 1 000 000 = 10⁶ см³.

Масса  1 м³  пробки  равна  0,2 · 10⁶ (г),  что  составляет  200 000 г или 200 кг. Значит, школьник не сможет поднять такую массу.

Ответ: нет.

4. Если разрезать кубический метр на кубические сантиметры и поставить их один на другой, то какой высоты получится столб?

При решении этой задачи следует использовать результаты предыдущей задачи.

IV. Итоги урока.

– Сформулируйте определение степени с натуральным показателем.

– Чему равна любая натуральная степень нуля?

– Каков порядок действий при нахождении числового и буквенного выражения, содержащего степень?

– Чему равно значение выражения 0,2⁸ · 5⁸? Как рационально вычислить? Каким правилом необходимо воспользоваться?

Домашнее задание: № 390; № 391; № 394; № 398.