
Пример решения задачи
Оптимизация сетевой модели
По данным варианта требуется:
1) построить сетевую модель;
2) определить критические пути модели;
3) провести максимально возможное уменьшение сроков выполнения проекта при минимально возможных дополнительных затратах;
|
Назв. работы |
Норм. длительность |
Норм. стоимость |
Сокр. длительность |
Повыш. стоимость |
|
А |
7 |
9 |
2 |
14 |
|
В |
6 |
16 |
1 |
18 |
|
С |
8 |
4 |
3 |
8 |
|
D |
9 |
11 |
4 |
12 |
|
Е |
10 |
14 |
4 |
18 |
|
F |
11 |
9 |
6 |
11 |
|
G |
5 |
13 |
1 |
19 |
|
H |
9 |
8 |
2 |
9 |
|
I |
12 |
15 |
5 |
17 |
|
J |
6 |
12 |
2 |
15 |
|
N = 13 человек |
Со = 149,00 руб. |
Ск = 1,30 руб,/день |
||
Упорядочение работ
1) G – исходная работа проекта;
2) Работы A,I и D следует за G и могут выполняться одновременно;
3) Работы С и J следует за А, работа F – за I, а работа В – за D;
4) Работа Е следует за С;
5) Работа Н следует за В, но не может начаться, пока не завершена F.
Где Ск - косвенные затраты; Со – ограничение по средствам.
Решение
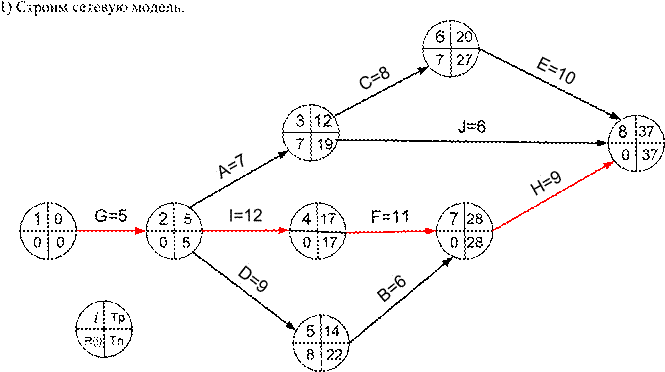
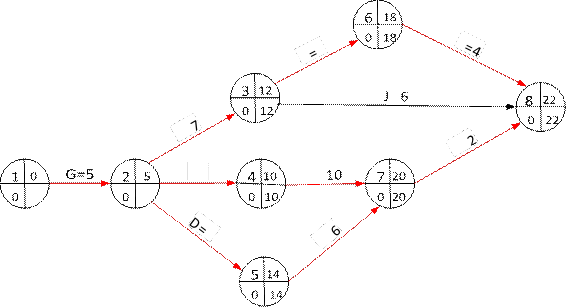
2) Критический путь G – I – F – H или 1 – 2 – 4 – 7 – 8 выделен красными дугами.
Длительность критического пути равна 5 + 12 + 11 + 9 = 37.
Прямые затраты при нормальной продолжительности работ составляют 111 руб., косвенные затраты – 1,30 руб,/день⋅37 дней = 48,10 руб., общие затраты – 159,1 руб.
3) Предположим, что все операции имеют нормальную продолжительность.
В сети имеется 4 пути из 1-го события в последнее.
Расположим их в порядке убывания длительностей:
1) L1 = {G,I,F,H} = {1,2,4,7,8}, 37 дней – критический;
2) L2 = {G,A,C,E} = {1,2,3,6,8}, 30 дней – подкритический;
3) L3 = {G,D,B,H} = {1,2,5,7,8}, 29 дней; 4) L4 = {G,A,J} = {1,2,3,8}, 18 дней.
Рассчитаем
удельные затраты на сокращение
продолжительности работ. Коэффициенты нарастания затрат, которые показывают затраты денежных средств, необходимые для сокращения
длительности работы (i, j) на один день,
вычислим по формуле k i j(
,
)
=
![]() Cc (i
j,
)−Cí
(i
j,
)
.
Cc (i
j,
)−Cí
(i
j,
)
.
Òí (i j, )−Òc (i j, )
|
Работа (i,j) |
Нормальная длительность |
Сокращённая длительность |
Нарастани е затрат |
Запас сокращен ия времени |
||
|
продолжи- телность, Tн |
стоимость, Cн |
продолжи- тельность, Тc |
стоимость, Сс |
|||
|
(2,3) – A |
7 |
9 |
2 |
14 |
1 |
5 |
|
(5,7) – B |
6 |
16 |
1 |
18 |
0,4 |
5 |
|
(3,6) – C |
8 |
4 |
3 |
8 |
0,8 |
5 |
|
(2,5) – D |
9 |
11 |
4 |
12 |
0,2 |
5 |
|
(6,8) – E |
10 |
14 |
4 |
18 |
2/3≈0,67 |
6 |
|
(4,7) – F |
11 |
9 |
6 |
11 |
0,4 |
5 |
|
(1,2) – G |
5 |
13 |
1 |
19 |
1,5 |
4 |
|
(7,8) – H |
9 |
8 |
2 |
9 |
1/7≈0,14 |
7 |
|
(2,4) – I |
12 |
15 |
5 |
17 |
2/7≈0,29 |
7 |
|
(3,8) – J |
6 |
12 |
2 |
15 |
0,75 |
4 |
|
|
|
Σ =111 |
|
|
|
|
Критические работы в таблице выделены.
1 шаг. Для сокращения выбираем критическую работу (7,8) – H с минимальным коэффициентом k(7,8) =1/7≈0,14 руб./день.
Текущий запас сокращения времени работы (7,8) на данном шаге равен 7 дней.
Разность между продолжительностью критического и подкритического путей 37–30=7 дней. Поэтому сокращаем работу (7,8) на ∆t1=min[7,7] = 7 дней. Новая текущая длительность работы (7,8) теперь 2 дня, а запас ее дальнейшего сокращения исчерпан.
После ускорения работы (7,8) возникли следующие изменения.
Затраты на работу H возросли на 1/7 руб./день ⋅ 7 дней = 1 руб., следовательно, прямые затраты теперь составляют 111+1=112 руб., косвенные затраты – 1,30 руб,/день⋅(37-7) дней = 39 руб., общие затраты – 151 руб. Длительность проекта теперь 37–7 = 30 дней.
Образовалось 2 критических пути с длительностью 30 дней.
1) L1 = {G,I,F,H} = {1,2,4,7,8}, 30 дней – критический;
2) L2 = {G,A,C,E} = {1,2,3,6,8}, 30 дней – критический; 3) L3 = {G,D,B,H} = {1,2,5,7,8}, 22 дня – подкритический; 4) L4 = {G,A,J} = {1,2,3,8}, 18 дней.
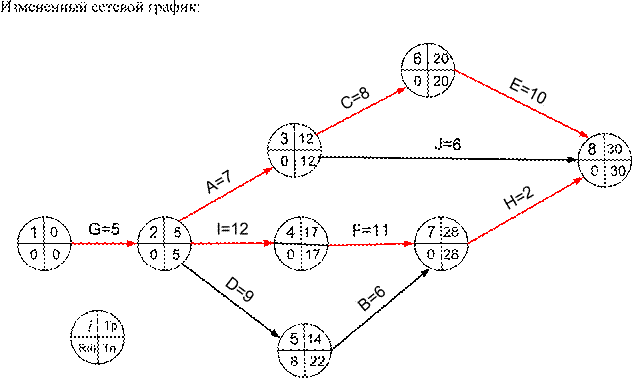
Изменённая таблица:
|
Работа (i,j) |
Нормальная длительность |
Сокращённая длительность |
Нарастани е затрат |
Запас сокращен ия времени |
||
|
продолжи- телность, Tн |
стоимость, Cн |
продолжи- тельность, Тc |
стоимость, Сс |
|||
|
(2,3) – A |
7 |
9 |
2 |
14 |
1 |
5 |
|
(5,7) – B |
6 |
16 |
1 |
18 |
0,4 |
5 |
|
(3,6) – C |
8 |
4 |
3 |
8 |
0,8 |
5 |
|
(2,5) – D |
9 |
11 |
4 |
12 |
0,2 |
5 |
|
(6,8) – E |
10 |
14 |
4 |
18 |
2/3≈0,67 |
6 |
|
(4,7) – F |
11 |
9 |
6 |
11 |
0,4 |
5 |
|
(1,2) – G |
5 |
13 |
1 |
19 |
1,5 |
4 |
|
(7,8) – H |
9 |
8 |
2 |
9 |
(1/7≈0,14) |
0 |
|
(2,4) – I |
12 |
15 |
5 |
17 |
2/7≈0,29 |
7 |
|
(3,8) – J |
6 |
12 |
2 |
15 |
0,75 |
4 |
|
|
|
Σ =111 |
|
Σ = 141 |
|
|
2 шаг.
Одновременное сокращение двух критических путей можно провести либо ускорив работу G(1,2), принадлежащую обоим путям, либо одновременно ускорив различные работы из каждого пути.
Ускорение работы G(1,2) обходится в 1,5 руб./день.
Наиболее дешевым вариантом является одновременное ускорение работ E(6,8) с нарастанием затрат 2/3≈0,67 руб./день и запасом сокращения времени в 6 дней и I(2,4) с нарастанием затрат 2/7≈0,29 руб./день и запасом сокращения времени в 7 дней.
Ускорение обеих этих работ на 1 день будет стоить 2/3+2/7 = 20/21≈0,95 руб./день.
Разность между продолжительностью критических и подкритического путей 30–22=8 дней, но сократить работы можно только на ∆t2=min[6,7,8] = 6 дней.
Новая текущая длительность работы E(6,8) теперь 10-6=4 дня, и запас ее дальнейшего сокращения исчерпан.
Новая текущая длительность работы I(2,4) теперь 12-6=6 дней, и она имеет ещё запас для дальнейшего возможного сокращения в 1 день.
После 2-го шага ускорения возникли следующие изменения.
Затраты возросли на 20/21 руб./день ⋅ 6 дней = 40/7≈5,71 руб., следовательно, прямые затраты теперь составляют 112+5,71=117,71 руб., косвенные затраты – 1,30 руб,/день⋅(30-6) дней = 31,2 руб., общие затраты – 148,9 руб. Длительность проекта теперь 30–6 = 24 дня.
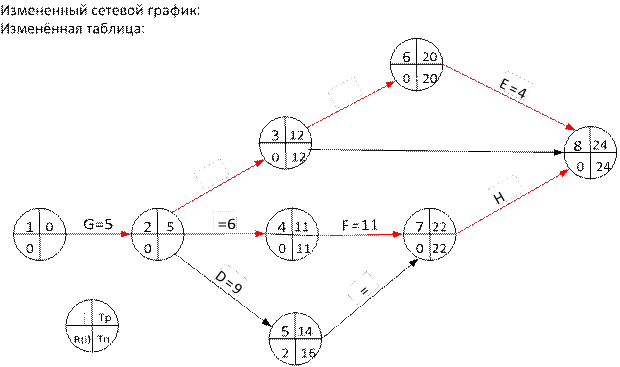
|
Работа (i,j) |
Нормальная длительность |
Сокращённая длительность |
Нарастани е затрат |
Запас сокращен ия времени |
||
|
продолжи- телность, Tн |
стоимость, Cн |
продолжи- тельность, Тc |
стоимость, Сс |
|||
|
(2,3) – A |
7 |
9 |
2 |
14 |
1 |
5 |
|
(5,7) – B |
6 |
16 |
1 |
18 |
0,4 |
5 |
|
(3,6) – C |
8 |
4 |
3 |
8 |
0,8 |
5 |
|
(2,5) – D |
9 |
11 |
4 |
12 |
0,2 |
5 |
|
(6,8) – E |
10 |
14 |
4 |
18 |
(2/3≈0,67) |
0 |
|
(4,7) – F |
11 |
9 |
6 |
11 |
0,4 |
5 |
|
(1,2) – G |
5 |
13 |
1 |
19 |
1,5 |
4 |
|
(7,8) – H |
9 |
8 |
2 |
9 |
(1/7≈0,14) |
0 |
|
(2,4) – I |
12 |
15 |
5 |
17 |
2/7≈0,29 |
1 |
|
(3,8) – J |
6 |
12 |
2 |
15 |
0,75 |
4 |
По прежнему осталось 2 критических пути с длительностью 24 дня.
1) L1 = {G,I,F,H} = {1,2,4,7,8}, 24 дня – критический;
2) L2 = {G,A,C,E} = {1,2,3,6,8}, 24 дня – критический; 3) L3 = {G,D,B,H} = {1,2,5,7,8}, 22 дня – подкритический; 4) L4 = {G,A,J} = {1,2,3,8}, 18 дней.
Поскольку существует ограничение на затраты в размере 149 руб., а на данном этапе общие затраты уже составляют 148,9 руб., то дальнейшая оптимизация может проходить только за счёт уменьшения косвенных расходов, т.е. не более, чем 1,30 руб./день.
3 шаг.
Одновременное сокращение двух критических путей можно провести либо ускорив работу G(1,2), принадлежащую обоим путям, либо одновременно ускорив различные работы из каждого пути.
Ускорение работы G(1,2) обходится в 1,5 руб./день, это больше, чем косвенные затраты на 1 день.
Произведём одновременное ускорение работ I(2,4) с нарастанием затрат 2/7≈0,29 руб./день и запасом сокращения времени в 1 день и С(3,6) с нарастанием затрат 0,8 руб./день и запасом сокращения времени в 5 дней.
Ускорение обеих этих работ на 1 день будет стоить 2/7+0,8=38/35≈1,09 руб./день.
Разность между продолжительностью критических и подкритического путей 24–22=2 дня, но сократить работы можно только на ∆t3=min[1,5,2] = 1 день.
Новая текущая длительность работы I(2,4) теперь составит минимальное для этой работы значение 5 дней, и запас ее дальнейшего сокращения будет исчерпан.
Новая текущая длительность работы С(3,6) теперь 8-1=7 дней, и она имеет ещё запас для дальнейшего возможного сокращения в 4 дня.
После 3-го шага ускорения возникли следующие изменения.
Прямые затраты возросли на 38/35≈1,09руб. и составляют теперь
112+5,71=117,71+1,09=118,8 руб., косвенные затраты 1,30 ⋅ 23 = 29,9 руб., общие затраты – 148,7 руб. Длительность проекта теперь 24–1 = 23 дня. Измененный сетевой график:
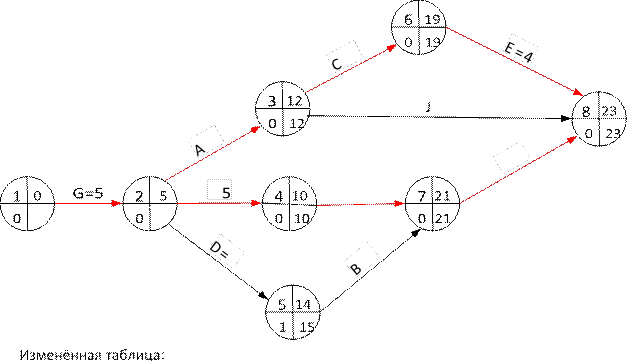
|
Работа (i,j) |
Нормальная длительность |
Сокращённая длительность |
Нарастани е затрат |
Запас сокращен ия времени |
||
|
продолжи- телность, Tн |
стоимость, Cн |
продолжи- тельность, Тc |
стоимость, Сс |
|||
|
(2,3) – A |
7 |
9 |
2 |
14 |
1 |
5 |
|
(5,7) – B |
6 |
16 |
1 |
18 |
0,4 |
5 |
|
(3,6) – C |
8 |
4 |
3 |
8 |
0,8 |
4 |
|
(2,5) – D |
9 |
11 |
4 |
12 |
0,2 |
5 |
|
(6,8) – E |
10 |
14 |
4 |
18 |
(2/3≈0,67) |
0 |
|
(4,7) – F |
11 |
9 |
6 |
11 |
0,4 |
5 |
|
(1,2) – G |
5 |
13 |
1 |
19 |
1,5 |
4 |
|
(7,8) – H |
9 |
8 |
2 |
9 |
(1/7≈0,14) |
0 |
|
(2,4) – I |
12 |
15 |
5 |
17 |
(2/7≈0,29) |
0 |
|
(3,8) – J |
6 |
12 |
2 |
15 |
0,75 |
4 |
По прежнему осталось 2 критических пути с длительностью 23 дня.
1) L1 = {G,I,F,H} = {1,2,4,7,8}, 23 дня – критический;
2) L2 = {G,A,C,E} = {1,2,3,6,8}, 23 дня – критический; 3) L3 = {G,D,B,H} = {1,2,5,7,8}, 22 дня – подкритический; 4) L4 = {G,A,J} = {1,2,3,8}, 18 дней.
4 шаг.
Произведём одновременное ускорение работ F(4,7) с нарастанием затрат 0,4 руб./день и запасом сокращения времени в 5 дней и С(3,6) с нарастанием затрат 0,8 руб./день и запасом сокращения времени в 4 дня.
Ускорение обеих этих работ на 1 день будет стоить 0,4+0,8=1,2руб./день.
Разность между продолжительностью критических и подкритического путей 23–22=1 день, поэтому ∆t4 =1 день.
Новая текущая длительность работы F(4,7) теперь составит 10 дней и она имеет ещё запас для дальнейшего возможного сокращения в 4 дня.
Новая текущая длительность работы С(3,6) теперь 7-1=6 дней, и она имеет ещё запас для дальнейшего возможного сокращения в 3 дня.
После 4-го шага ускорения возникли следующие изменения.
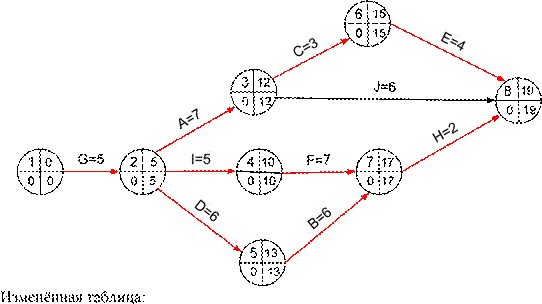
Прямые затраты возросли на 1,2 руб. и составляют теперь 118,8+1,2=120 руб., косвенные затраты 1,30 ⋅ 22 = 28,6 руб., общие затраты – 148,6 руб. Длительность проекта теперь 22 дня.
Измененный сетевой график:
Изменённая таблица:
|
Работа (i,j) |
Нормальная длительность |
Сокращённая длительность |
Нарастани е затрат |
Запас сокращен ия времени |
||
|
продолжи- телность, Tн |
стоимость, Cн |
продолжи- тельность, Тc |
стоимость, Сс |
|||
|
(2,3) – A |
7 |
9 |
2 |
14 |
1 |
5 |
|
(5,7) – B |
6 |
16 |
1 |
18 |
0,4 |
5 |
|
(3,6) – C |
8 |
4 |
3 |
8 |
0,8 |
3 |
|
(2,5) – D |
9 |
11 |
4 |
12 |
0,2 |
5 |
|
(6,8) – E |
10 |
14 |
4 |
18 |
(2/3≈0,67) |
0 |
|
(4,7) – F |
11 |
9 |
6 |
11 |
0,4 |
4 |
|
(1,2) – G |
5 |
13 |
1 |
19 |
1,5 |
4 |
|
(7,8) – H |
9 |
8 |
2 |
9 |
(1/7≈0,14) |
0 |
|
(2,4) – I |
12 |
15 |
5 |
17 |
(2/7≈0,29) |
0 |
|
(3,8) – J |
6 |
12 |
2 |
15 |
0,75 |
4 |
Теперь образовалось 3 критических путей с длительностью 22 дня.
1) L1 = {G,I,F,H} = {1,2,4,7,8}, 22 дня – критический;
2) L2 = {G,A,C,E} = {1,2,3,6,8}, 22 дня – критический;
3) L3 = {G,D,B,H} = {1,2,5,7,8}, 22 дня – критический; 4) L4 = {G,A,J} = {1,2,3,8}, 18 дней – подкритический.
5 шаг.
Произведём одновременное ускорение 3-х работ на 3-х критических путях: 1) D(2,5) с нарастанием затрат 0,2 руб./день и запасом сокращения времени в 5 дней; 2) F(4,7) с нарастанием затрат 0,4 руб./день и запасом сокращения времени в 4 дня;
3) С(3,6) с нарастанием затрат 0,8 руб./день и запасом сокращения времени в 3 дня.
Ускорение всех этих работ на 1 день будет стоить 0,4+0,2+0,8=1,4руб./день.
Разность между продолжительностью критических и подкритического путей 22–18=4 дня, поэтому ∆t5=min[5,4,3,4] = 3 дня.
Новая текущая длительность работы D(2,5) теперь составит 6 дней и она имеет ещё запас для дальнейшего возможного сокращения в 2 дня.
Новая текущая длительность работы F(4,7) теперь составит 7 дней и она имеет ещё запас для дальнейшего возможного сокращения в 1 день.
Новая текущая длительность работы С(3,6) теперь 3 дня, и она исчерпала свой запас для дальнейшего сокращения.
После 5-го шага ускорения возникли следующие изменения.
Прямые затраты возросли на 1,4⋅3=4,2 руб. и составляют теперь 124,2 руб., косвенные затраты 1,30 ⋅ 19 = 24,7 руб., общие затраты – 148,9 руб. Длительность проекта теперь 19 дней.
Измененный сетевой график:
|
Работа (i,j) |
Нормальная длительность |
Сокращённая длительность |
Нарастани е затрат |
Запас сокращен ия времени |
||
|
продолжи- телность, Tн |
стоимость, Cн |
продолжи- тельность, Тc |
стоимость, Сс |
|||
|
(2,3) – A |
7 |
9 |
2 |
14 |
1 |
5 |
|
(5,7) – B |
6 |
16 |
1 |
18 |
0,4 |
5 |
|
(3,6) – C |
8 |
4 |
3 |
8 |
(0,8) |
0 |
|
(2,5) – D |
9 |
11 |
4 |
12 |
0,2 |
2 |
|
(6,8) – E |
10 |
14 |
4 |
18 |
(2/3≈0,67) |
0 |
|
(4,7) – F |
11 |
9 |
6 |
11 |
0,4 |
1 |
|
(1,2) – G |
5 |
13 |
1 |
19 |
1,5 |
4 |
|
(7,8) – H |
9 |
8 |
2 |
9 |
(1/7≈0,14) |
0 |
|
(2,4) – I |
12 |
15 |
5 |
17 |
(2/7≈0,29) |
0 |
|
(3,8) – J |
6 |
12 |
2 |
15 |
0,75 |
4 |
Остались те же 3 критических путей с новой длительностью 19 дней.
1) L1 = {G,I,F,H} = {1,2,4,7,8}, 19 дня – критический;
2) L2 = {G,A,C,E} = {1,2,3,6,8}, 19 дня – критический;
3) L3 = {G,D,B,H} = {1,2,5,7,8}, 19 дня – критический; 4) L4 = {G,A,J} = {1,2,3,8}, 18 дней – подкритический.
6 шаг.
Возможностей для дальнейшего ускорения теперь не осталось, т.к. ускорение общей работы G(1,2) обходится в 1,5 руб./день, это больше, чем косвенные затраты на 1 день, а дальнейшая оптимизация может проходить только за счёт уменьшения косвенных расходов, т.е. не более, чем 1,30 руб./день.
Если производить одновременное ускорение 3-х работ на 3-х критических путях, то можно выбрать следующие оставшиеся работы с минимальными коэффициент нарастания затрат: 1) D(2,5) с нарастанием затрат 0,2 руб./день и запасом сокращения времени в 2 дня;
2) F(4,7) с нарастанием затрат 0,4 руб./день и запасом сокращения времени в 1 день; 3) A(2,3) с нарастанием затрат 1 руб./день и запасом сокращения времени в 5 дней. Ускорение всех этих работ на 1 день будет стоить 0,4+0,2+1=1,6 руб., а экономия на косвенных расходах за 1 день составит 1,30 руб., т.е. общие расходы при такой оптимизации составят 148,9+1,6–1,3 = 149,2 руб., что превышает установленный лимит в 149 руб.
Результаты оптимизации следующие:
Выполнение всего комплекса работ занимает теперь 19 дней, стоимость выполнения работ составляет 148,9 руб. Таким образом, удалось сократить время выполнения проекта на 18 дней и общие затраты за счёт уменьшения косвенных расходов тоже сократились с 159,1 руб. при нормальном режиме работы до 148,9 руб. при ускоренном режиме, т.е. на 10,2 руб.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.