Ориентированные и неориентированные графы. Дерево, корень, вершина, лист, ребро (дуга) дерева

23-24 урок, 9 класс

Учитель: Брух Т.В.

Дата: ____________

Тема урока: «Ориентированные и неориентированные графы. Дерево, корень, вершина, лист, ребро (дуга) дерева»

Цель урока: расширить представления у учащихся о видах информационных моделей, сформировать представление о графах как наглядном средстве представления структуры и состава системы. 

Задачи урока:

·        Образовательные: обеспечить усвоение учащимися знаний о графах, отработать навыки построения графов;

·        Развивающие: развить познавательные интересы, навыки работы в MSOfficeWord, самоконтроль и умение работать в группе; сформировать умение выделять существенные признаки и свойства, а также отличать несущественные и отвлекаться от них; развитие приемов умственной деятельности, логического и пространственного мышления, внимания, навыков коммуникативной работы.

·        Воспитательные: вызвать у учащихся стремление активно принимать участие в усвоении новой темы, мотивировать на потребность в самостоятельной исследовательской деятельности.

Ход урока:

1. Организационный момент

Здравствуйте, ребята. Садитесь. Сегодня на уроке мы проверим ранее изученную вами тему, затем изучим новый материал, закрепим его и выполним практическую работу, после чего подведем итоги урока. Для начала отметим отсутствующих.

2. Изложение нового материала 

Теперь мы с вами перейдем к изучению нового материала. Открывайте тетради, записывайте тему урока: «Ориентированные и неориентированные графы. Дерево, корень, вершина, лист, ребро (дуга) дерева».

Ребята, как вы считаете, есть ли что-то общее у диаграмм, графиков, схем и графов?

Да, есть. Они служат для визуализации данных, для наглядного представления.

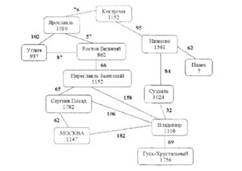
Посмотрите внимательно на слайд. Перед вами представлена схема городов, которые входят в состав городов Золотого кольца России. Данная схема называется графом. Рассмотрим другие графы.

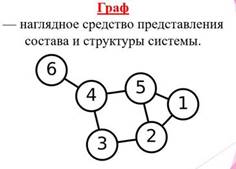
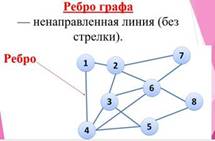
Посмотрите на слайд. Перед вами изображен граф.

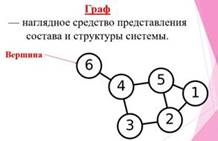
Граф состоит из вершин, связанных линиями.

Направленная линия (со стрелкой) называется дугой.

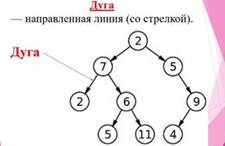Ненаправленная линия (без стрелки) называется ребром.

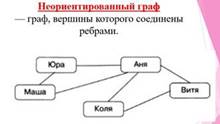Граф называется неориентированным, если его вершины соединены ребрами.

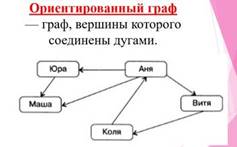Граф называется ориентированным, если его вершины соединены дугами.

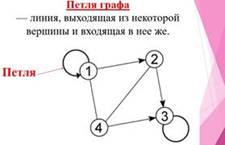Линия, выходящая из некоторой вершины и входящая в нее же, называется петлей.

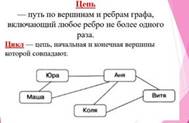
Путь по вершинам и ребрам графа, включающий любое ребро графа не более одного раза, называется цепью. (Например, Юра — Аня — Витя — Коля).

Цепь, начальная и конечная вершины которой совпадают, называется циклом. (Например, Аня — Коля — Витя — Аня).

Граф называется взвешенным, если его вершины или ребра (дуги) характеризуются некоторой дополнительной информацией – весом вершины или ребра (дуги). Предположим, что наш граф – это информация о городах Золотого кольца. Веса его вершин – года основания городов, веса ребер – расстояния в километрах между городами.

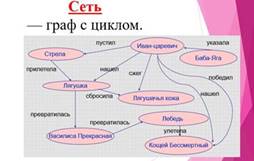Граф с циклом называется сетью.

3.  Закрепление материала

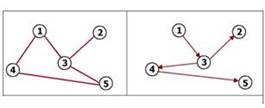Ребята, посмотрите на слайд, ответьте, что вы видите?

Граф.

Верно, а назовите вид этих графов?

1 - неориентированный, 2 – ориентированный.

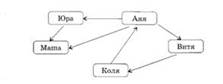Хорошо. Перед вами граф. Назовите, какой путь в данном случае будет называться цепью, а какой циклом?

Цепь: Аня — Юра — Маша. Цикл: Аня — Витя — Коля — Аня.

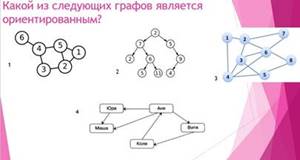
Молодцы. Теперь вам предстоит ответить, какой из предложенных графов, является ориентированным?

4. Практическая работа

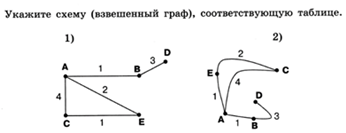
1.     Задание:

2.     Задание:

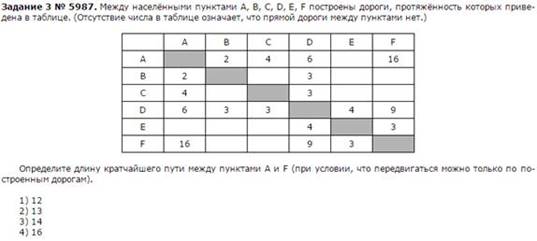
3.     Задание:

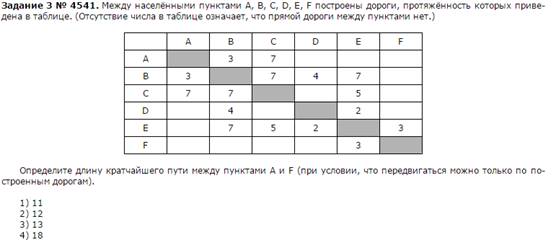
4.     Задание:

5. Задание:

5.  Итог урока.

Домашнее задание