Основное уравнение МКТ

                                                Занятие 22

Тема. Основное уравнение молекулярно-кинетической теории газов.

Связь между давлением идеального газа и средней кинетической энергией теплового движения его молекул.

Цели: усвоить понятия идеального газа, основное уравнение МКТ;  на основе МКТ установить количественную зависимость давления газа от массы одной молекулы и среднего квадрата скорости ее движения; воспитывать ответственное отношение к учебе, положительное отношение к предмету физики.

Тип занятия: комбинированный.

Ход занятия.

1. Организационный момент.

2.Проверка домашнего задания

Упражнение 11 (5)

Чему равно число молекул в 10 г кислорода?

Дано:                                                       Решение:

m=10 г =10·10^-3 кг                                N=N_a·m/M= 6,02·10²³ ·10^-4/32·10^-3 =1,8·10²³

М=32·10^-3 кг/моль

N=?

                                                                         Ответ: 1,8·10²³

3. Знакомство аудитории с темой и целью занятия.

Мотивация учебной деятельности студентов.

4 .Изучение нового материала.

1. Макроскопические параметры.

Состояние газа (так же как жидкости и твердого тела) может быть описано и без рассмотрения молекулярного строения вещества. Это делают с помощью макроскопических величин, совокупность которых однозначно определяет состояние системы. Такие величины называют параметрами состояния (или термоди­намическими параметрами). Параметрами состояния любой системы являются ее объем, давление и температура. Если в каком-либо процессе изменяется хотя бы один из параметров состояния системы, то и само состояние системы становится другим.

Величины, характеризующие состояние макроскопических тел без учета их внутреннего строения называются макроскопическими параметрами.

Все газы при не слишком высоких давлениях и при не слишком низких температурах близки по своим свойствам к идеальному газу. При высоких давлениях молекулы газа настолько сближа­ются, что пренебрегать их собственными размерами нельзя. При понижении температуры кинетическая энергия молекул уменьшается и становится сравнимой с их потенциальной энер­гией, следовательно, при низких температурах пренебрегать по­тенциальной энергией нельзя.

При высоких давлениях и низких темпера­турах газ не может считаться идеальным. Такой газ называют реальным. (Поведение реального газа описывается законами, отличающимися от законов идеального газа.)

2. Идеальный газ

Известно, что частицы в газах, в отличие от жидкостей и твердых тел, располагаются друг относительно друга на расстояниях, существенно превышающих их собственные размеры. В этом случае взаимодействие между молекулами пренебрежимо мало и кинетическая энергия молекул много больше энергии межмолекулярного взаимодействия. Для выяснения наиболее общих свойств, присущих всем газам, используют упрощенную модель реальных газов - идеальный газ. Основные отличия идеального газа от реального газа:

1. Частицы идеального газа - сферические тела очень малых размеров, практически материальные точки.
2. Между частицами отсутствуют силы межмолекулярного взаимодействия.
3. Соударения частиц являются абсолютно упругими.

Сле­ду­ет от­ме­тить, что раз­ре­жен­ный во­до­род (под очень ма­лень­ким дав­ле­ни­ем) прак­ти­че­ски пол­но­стью удо­вле­тво­ря­ет мо­де­ли иде­аль­но­го газа

2. Основное уравнение молекулярно-кинетической теории идеального газа.

Давление газа определяется столкновением молекул газа со стенками сосуда.

В СИ за единицу давления принимают 1 Па.

Давление, при котором на площадь 1 м² действует сила давления в 1 Н, называется Паскалем.

1мм. рт. ст. = 133 Па

1атм = 101325 Па

     Основная задача молекулярно-кинетической теории газа заключается в том, чтобы установить соотношение между давлением газа и его микроскопическими параметрами - массой молекул, их средней скоростью и концентрацией. Это соотношение называется основным уравнением молекулярно-кинетической теории газа.

Поскольку давление газа на стенку сосуда обусловлено ударами молекул, давление газа пропорционально концентрации молекул n: чем больше молекул в единице объема, тем больше ударов молекул о стенку за единицу времени. Каждая молекула при ударе о стенку передает ей импульс, пропорциональный импульсу молекулы, равном по модулю m₀υ, где υ- модуль скорости молекулы. Поэтому можно было бы ожидать, что давление пропорционально nm₀υ, где υ- среднее значение модуля скорости молекул.

Однако, на самом деле давление пропорционально не первой, а второй степени скорости, так как, чем больше скорость молекулы, тем чаще она бьется о стенку сосуда. И действительно, расчеты показывают, что основное уравнение молекулярно-кинетической теории идеального газа имеет вид:

где m₀ - масса одной молекулы газа, n - концентрация молекул,  - среднее значение квадрата скорости молекул.

Коэффициент 1/3 обусловлен трехмерностью пространства - тем, что во время хаотического движения молекул все три направления равноправны.

Итак, немецкий физик Г. Клаузиус выяснил, что давление идеального газа прямо пропорционально концентрации частиц, массы частицы и среднего значения квадрата скорости частицы.

Полученное уравнение связывает макроскопічну величину - давление,- что может быть измерено манометром, с микроскопическими величинами, характеризующими молекулы, и является как бы мостиком между двумя мирами: макроскопическим и микроскопическим.

3. Связь давления со средней кинетической энергией молекулы

Если через обозначить среднюю кинетическую энергию поступательного движения молекулы, 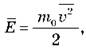то уравнение Клапейрона можно записать в виде:

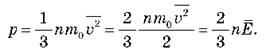
Давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы В этой формуле концентрация частиц характеризует число ударов молекул о поршень, а средняя кинетическая энергия молекул определяет интенсивность одного удара.

 4. Решение задач.

Задача №1.

Кислород находится в нормальных условиях. Вычислите среднюю квадратичную скорость молекул газа.

Решение.

При нормальных условиях давление кислорода равна 1,01·105 Па, а плотность - 1,43 кг/м3. Считая, что концентрация газа n = N/V, можно записать:

Отсюда получаем:

Проверив единицы величин и выполнив расчеты, получаем = 460 м/с.

Задача №2. Определите кинетическую энергию хаотического поступательного движения всех молекул любого газа в баллоне объемом 5 л с давлением 1 МПа.

Задача №3. Чему равна средняя кинетическая энергия хаотического движения молекул аргона, если 2 кг его, находясь в сосуде объемом 2 м3, оказывают давление 3·105 Па?

5. Закрепление изученного на занятии.

1.Что такое макроскопические параметры?

2. Какие величины относятся к их числу?

3.Изменяется ли состояние системы при изменении одного такого параметра?

4.  Какой газ называют идеальным? Что является моделью идеального газа?

5.  При каких условиях газ по своим свойствам близок к идеальному? При каких условиях и почему газ не может считаться идеальным?

6.Каков механизм возникновения давления газа с точки зрения молекулярно-кинетической теории строения вещества?

7. Почему можно считать, что молекулы в газе движутся только вдоль трех взаимно перпендикулярных направлений?

6. Задание на дом.

§ 61,  § 63, Физика 10 класс Г.Я. Мякишев,  Б.Б Буховцев, записи в тетради, упр. 11 (задачи 8,9) 

Скачано с www.znanio.ru