
18. a mod a = 0 (6)
19. (a + b) mod N = (a mod N + b mod N) mod N (7)
20. (a – b) mod N = (a mod N – b mod N) mod N (8)
21. (a * b) mod N = (a mod N) * (b mod N) mod N (9)
Доказательство — прямая подстановка. Например:
a = 60, b = 63, N = 32
(60 * 63) mod 32 =3780 mod 32 =3780 – 32 * 118 = 4 L mod N = L – N * INT(L/N)
60 mod 32 = 28, 63 mod 32 = 31
(28 * 31) mod 32 = 868 mod 32 = 4
Следствие:
Если m = a + b + c, то:
22. xm mod N = xa+b+c mod N = (xaxbxc) mod N =
= [(xa mod N)*(xb mod N)*(xc mod N)] mod N (10)
23. (a*(b+c)) mod N = ((a*b) mod N + (a*c) mod N) mod N (11)
24. xa×i mod N = (xa mod N)i mod N) (12)
Действительно, например 52×3 mod 11 = 56 mod 11 = 5
52 mod 11 = 3
(52 mod 11)3 mod 11 = 33 mod 11 = 27 mod 11 = 5
Формулы (9), (10), (12) удобно использовать для расчета по mod N больших чисел превосходящих разрядность ЭВМ.
Например: x53 mod N
Разложим 53 на двоичные сомножители 1, 2, 4, 8, 32, 64, …. x53 = x(32+16+4+1)
Надо сачала найти x2, x4 = (x2)2, x8 = (x4)2, x16 = (x8)2, x32 = (x16)2.
Это 5 операций умножения.
Теперь надо последовательно умножить 32
16 x 4 × x
еще три операции умножения. Все
операции надо делать по модулю N. Получим результат за 8 операций
Пример 1:
319 mod 15 = 319 — 15×Int(319/15) = 1162261467 – 15×77484097= 12
19 = 16 + 2 + 1
|
1 |
3 |
3 |
|
|
2 |
32 = 9 |
9 |
3×9 = 27 mod 15 = 12 |
|
4 |
92 = 81 mod 15 = 6 |
|
|
|
8 |
62 = 36 mod 15 = 6 |
|
|
|
16 |
62 = 36 mod 15 = 6 |
6 |
12×6 = 72 mod 15 = 12 |
Следствие: если xa mod N = 1, то и xa×i mod N = 1
Пример 2:
Общие формулы вычисления больших степеней.
ab mod N = (a×a×а×…×a (b раз) mod N) затем применяем формулу (9)
25. F(φ(x)) mod N = F(φ(x) mod N) mod N (13)
Проверка: N = 11, x = 5
|
φ(x) = x2 |
φ(x) mod N = 52 mod 11 = 3 |
F(φ(x)) mod N = (10*25) mod 11 = |
|
F(y) = 10y |
F(y) mod N = 10*3 mod 11 = 8 |
= 250 mod 11 = 8 |
26. Свойство коммутативности. Обозначим xa mod N = Fa(x), xb mod N = Fb(x) Будет верно тождество
Fa(Fb(x)) mod N = Fb(Fa(x)) mod N для всех x. (14)
Действительно:
Fa(Fb(x)) = (Fb(x))a mod N = (xb mod N)a mod N = (см. формулу 13) = (xb)a mod N = xba mod N Fb(Fa(x)) = (Fa(x))b mod N = (xa mod N)b mod N = (см. формулу 13) = (xa)b mod N = xab mod N
но xba = xab следовательно и Fa(Fb(x)) = Fb(Fa(x))
27. Теорема Эвклида (300 г. до н.э.)
Если Е и М удовлетворяют условию 0 < EM и НОД(М,Е) = 1, то существует единственное число D, такое что 0 < D < M и
E*D º 1 (mod M) ((E*D) mod M = 1) (15)
и кроме того D может быть вычислено с помощью расширения алгоритма Евклида при нахождении HOD(M, Е). (Сравни Кнут Д. ”Искусство программирования, ” т. 1 стр. 26, 1976г.
Алгоритм Евклида при нахождении HOD (M,Е).
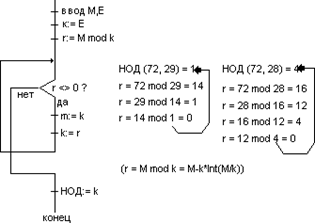
Рисунок 3.2
28. Функция Эйлера
Φ(N) — функция Эйлера определяет для каждого положительного целого числа N количество положительных целых чисел i не превышающих N и таких, что HOD(i,N) = 1, При N = 1 по определению Φ (1) = 1
1 £ i < N
Найдем, например, Φ(8). Вычислим НОД (i, 8), 1 £ i < 8, (i = 1, 2, …7)
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
НОД (i,8) |
1 |
2 |
1 |
4 |
1 |
2 |
1 |
Имеем до 4-х i = 1, 3, 5, 7 НОД (i,8) = 1 следовательно Φ(8) = 4.
Очевидно, что для простого числа Р имеем Φ(Р) = Р – 1, так как простое число не делится нацело на меньшее число. Например, Φ(7) = 7 – 1 = 6, ибо для всех i=1,2,3,4,5,6 НОД(i,7) = 1.
Нетрудно видеть, что для двух неравных простых чисел P и Q
Φ(P*Q) = (P- 1)*(Q – 1) (16)
Например, Φ(6) = Φ(2*3) = 1*2 = 2.
29. Теорема Эйлера
Для любых целых чисел x и N (x < N)
xΦ(N) º 1 (mod N), xΦ(N) mod N = 1 (17)
при условии, что НОД (x, N) = 1.
Например, для Φ(8) = 4 сравнение (17), будет выполнено только для x = 1,3,5,7 для которых НОД (х, N) = 1.
Действительно, например :
для х = 2 : 2Φ(8) mod 8 = 24 mod Φ = 16 mod 8 = 0
а для х = 3 : 34 mod 8 = 81 mod Φ = 1.Генерация псевдослучайных последовательностей (ПСП) чисел и бит
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.