Основы фракталов и их компьютерные модели

ОСНОВЫ ФРАКТАЛОВ И ИХ КОМПЬЮТЕРНЫЕ МОДЕЛИ

Аннотация: в данной работе исследуются фрактальные структуры, проводится анализ их свойств и создаётся компьютерная программа для их построения.

Ключевые слова: фрактал, фрактальная размерность, самоподобие, L-системы.

Изучая геометрию, мы зачастую приходим к выводу, что она часто бывает излишне «сухой» и «правильной».

Прямые, фигуры, теоремы, леммы и т.д. – все чётко, правильно, прямо. А так ли все правильно и строго в реальном мире? Нет! Облака – отнюдь не сферы, береговые линии нельзя описать гладкой кривой…

Рассмотрев большое число природных объектов, мы можем утверждать, что многие из них настолько «нестандартны», что, по сравнению с со стандартной геометрией, – природа обладает не просто большей сложностью, а сложностью совершенно иного уровня. В таких случаях, на помощь нам приходит фрактальная геометрия.

Цель нашего исследования – понять какими законами теории фракталов можно описать реальные природные объекты и, если таковые найдутся, попытаться создать на их основе компьютерную модель.

В начале исследования нами была рассмотрена береговая линия Северной Двины в близи города Котласа с использованием сервиса Яндекс.Карты.

Первоначально мы измерили её длину в масштабе 1см:3км. Расстояние от автомобильного моста до точки слияния Северной Двины и Вычегды составило 7км 60м (рис.1). При уменьшении масштаба до 1см:500м расстояние увеличилось до 7км 120м, при масштабе 1см:35м длина между этими точками составила уже 7км 340м. (рис.2)

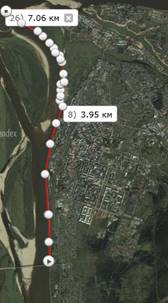
Рис. 1

Рис. 2

Т.е., по мере того, как мы уменьшаем масштаб, длина береговой линии увеличивается, и объективного предела уменьшению масштаба (и, тем самым, увеличению длины береговой линии) просто не существует; мы вынуждены были признать, что эта линия имеет бесконечную длину.

Из геометрии нам известно, что традиционные геометрические объекты имеют целочисленную размерность (степень уравнения для его описания): линия одномерна, плоская поверхность двумерна и т.д.

Изучая литературу по данной теме мы пришли к выводу, что линии, подобные береговой выходят за одномерного пространства, частично заполняя двумерное. Т.е. их размерность (D):

.

Иными словами, это дробь. Учёные называют коэффициент D фрактальной размерностью. Слово фрактал происходит от латинского слова fractal – дробный, нецелый. [2]

Одним из основных свойств является свойство самоподобия. Изучим, в чём оно заключается.

Самоподобная геометрическая фигура может быть поделена на части, каждая из которых будет представлять, по крайней мере, приблизительно, уменьшенную копию целого. Т.е. фрактал – это такой объект, для которого не важно, с каким усилением его рассматривать в увеличительное стекло, при всех его увеличениях структура остаётся одной и той же.

При дальнейшем исследовании, мы выяснили, что фракталы делятся на группы. Основные из них – геометрические и алгебраические. [2]

Ввиду достаточной сложности математического описания и построения алгебраических фракталов, дальнейшее исследование было направлено только на геометрические.

Этот тип фракталов получается путём простых геометрических построений. Обычно при построении этих фракталов используется «затравка» (аксиома) – набор отрезков, на основании которых будет строиться фрактал. Далее к этой «затравке» применяют набор правил, который преобразует её в какую-либо геометрическую фигуру. Далее к каждой части этой фигуры применяют опять тот же набор правил и т.д. С каждым шагом фигура будет становиться все сложнее и сложнее, сохраняя свойство самоподобия. [1]

Далее мы приступили к реализации алгоритма построения геометрического фрактала. Сам алгоритм был описан следующим образом:

1.          нарисовать фигуру,

2.          части фигуры заменить на уменьшенные копии этой фигуры,

3.          повторить второй шаг.

Для компьютерной реализации был выбран метод L-систем, при котором движение строится пошагово относительно текущей точки и каждое единичное движение заменяется на весь рисунок. [1]

Для создания программы по такому принципу идеально подойдёт среда исполнителя «Чертёжник».

Нами были реализованы 2 фрактала: дерево Пифагора и фрактал «Ветка». (рис.3)

Рис. 3

Как видите, созданные фракталы достаточно близко повторяют реальные природные объекты.

Фракталы очень широко используются в создании компьютерных изображений. Кроме того, их можно применять в моделировании структур, имеющих признаки самоподобия (кровеносная система человека, например).

Список литературы:

1.     Морозов А.Д. Введение в теорию фракталов. – М., 2002. – 389 c.

2.     Мандельброт Б. Фрактальная геометрия природы. – М., 2002. – 666 c.

3.     Скачано с www.znanio.ru