Особенности представления чисел в компьютере. Хранение в памяти целых чисел

11-12 урок, 10 класс – теория

Учитель: Брух Т.В.

Дата: ___________

Тема: «Особенности представления  чисел в компьютере. Хранение в памяти целых чисел»

Цель урока: иметь представление о форматах чисел с фиксированной и плавающей запятой (точкой), знать понятия прямого кода, обратного кода, дополнительного кода, уметь записывать целые числа (положительные и отрицательные) в прямом, обратном и дополнительном коде.

Задачи урока:

·      образовательные:  закрепление знаний учащихся по теме «Представление целых чисел в компьютере».

·      развивающие:  совершенствование умственной и познавательной деятельности учащихся, развитие мышления учащихся.

·      воспитательные: сознательное усвоение материала учащимися.

Ход урока:

1. Организационный момент.

2. Изучение нового материала

1). Целые числа. Представление чисел в формате с фиксированной точкой.

Фиксированная точка.

Целые числа в компьютере хранятся в памяти в формате с фиксированной запятой или фиксированной точкой. В этом случае каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а запятая находится справа после младшего разряда, т.е. вне разрядной сетки.

Для хранения целых неотрицательных чисел отводится одна ячейка памяти (8 битов). Например, число А₂ =  11110000₂ будет храниться в ячейке памяти следующим образом:

Максимальное значение целого неотрицательного числа достигается в случае, когда во всех ячейках хранятся едини­цы. Если в первых двух ячейках 11, а в остальных 0, то значение числа будет равно 3, если число представлено как 111, то значение числа 7, если единицами занято 8 разрядов, то значение числа равно 2 ⁸  -1 =256-1=255, так как отсчет начинается с 0.

Для п-разрядного представления оно будет равно 2ⁿ -1.

Это можно доказать и по-другому:

Максимальное число соответствует восьми едини­цам и равно

А = 1▪2⁷ +1▪2⁶ +1▪2⁵ + 1▪2⁴ + 1▪2³ + 1▪2² + 1▪2¹ + 1▪2° = 1▪2⁸ - 1 = 255₁₀.

Диапазон изменения целых неотрицательных чисел: от 0 до 255.

Итак, целые числа могут представляться в компьютере со знаком или без знака.

Целые числа без знака обычно занимают в памяти один или два байта и принимают в однобайтовом формате значения от 00000000₂ до 11111111₂, а в двубайтовом формате — от 00000000 00000000₂ до 11111111 11111111₂.

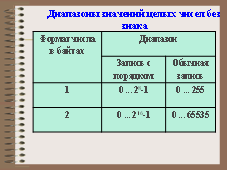
Диапазоны значений целых чисел без знака

Примеры:

а) число 72₁₀ = 1001000₂ в однобайтовом формате:

б) это же число в двубайтовом формате:

в) число 65535 в двубайтовом формате:

Представление целых положительных чисел.

Алгоритм№1.  Получения внутреннего представления целого положительного числа N, хранящегося в k разрядном машинном слове:

1. Перевести число N в двоичную систему счисления.

2. Полученный результат дополнить слева незначащими нулями до k  разрядов.

Представление целых чисел со знаком. Прямой код числа.

Для хранения целых чисел со знаком отводится две ячей­ки памяти (16 битов), причем старший (левый) разряд отво­дится под знак числа (если число положительное, то в знако­вый разряд записывается 0, если число отрицательное — 1).

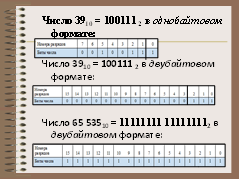
Число 39₁₀ = 100111 ₂ в однобайтовом формате:

    Число 39₁₀ = 100111 ₂ в двубайтовом формате:

Число 65 535₁₀ = 11111111 11111111₂ в двубайтовом формате:

Максимальное положительное число (с учетом выделения одного разряда на знак) для целых чисел со знаком в n-раз­рядном представлении равно:

А = 2^{п -1} - 1. (один разряд на знак).

Целые числа со знаком обычно занимают в памяти компьютера один, два или четыре байта, при этом самый левый (старший) разряд содержит информацию о знаке числа. Знак “плюс” кодируется нулем, а “минус” — единицей.

Диапазоны значений целых чисел со знаком

Числа, для хранения которых отводится четыре ячейки памяти –32 бита,  это числа, хранящиеся в оперативной памяти в формате длинных целых чисел со знаком. Значения минимального отрицательного и максимального положительного чисел ограничены. Это недостаток представления чисел в формате с фиксированной  запятой.

Алгоритм№2 .Получение внутреннего представления целого числа со знаком,  хранящегося в k разрядном машинном слове (запись числа в прямом коде):

1.      Перевести число N в двоичную систему счисления.

2.      Полученный результат дополнить слева незначащими нулями до k-1  разрядов.

3.      Записать в самый левый (старший) разряд информацию о знаке числа: знак “плюс” кодируется нулем, а “минус” — единицей.

Дополнительный код. Обратный код.

Итак, в компьютерной технике применяются три формы записи (кодирования) целых чисел со знаком:

·               прямой код (в формате «знак-величина»),

·               обратный код (получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули заменяются единицами, а единицы — нулями,

·               дополнительный код (получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду).

Для представления отрицательных чисел используется  дополнительный код. Дополнительный код позволяет заменить арифметическую операцию вычитания операцией сложения, что существенно упрощает работу процессора и увеличивает его быстродействие. Последние две формы применяются особенно широко, так как позволяют упростить конструкцию арифметико-логического устройства компьютера путем замены разнообразных арифметических операций операцией cложения.

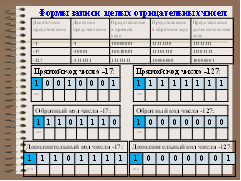
Рассмотрим особенности записи целых чисел со знаком на примере однобайтового формата, при котором для знака отводится один разряд, а для цифр абсолютной величины – семь разрядов.

Положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково — двоичными кодами с цифрой 0 в знаковом разряде.

Например:

Слайд №9

Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение.

1. Прямой код. В знаковый разряд помещается цифра 1, а в разряды цифровой части числа — двоичный код его абсолютной величины. Например:

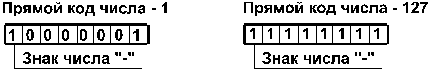
2. Обратный код. Получается инвертированием всех цифр двоичного кода абсолютной величины числа (модуля числа), включая разряд знака: нули заменяются единицами, а единицы — нулями. Например:

3. Дополнительный код. Получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду. Например:

Обычно отрицательные десятичные числа при вводе в машину автоматически преобразуются в обратный или дополнительный двоичный код и в таком виде хранятся, перемещаются и участвуют в операциях. При выводе таких чисел из машины происходит обратное преобразование в отрицательные десятичные числа.

3) Как компьютер выполняет арифметические действия над целыми числами?

Сложение и вычитание

В большинстве компьютеров операция вычитания не используется. Вместо нее производится сложение уменьшаемого с обратным или дополнительным кодом вычитаемого. Это позволяет существенно упростить конструкцию АЛУ.

    При сложении обратных кодов чисел А и В имеют место четыре основных и два особых случая:

1. А и В положительные. При суммировании складываются все разряды, включая разряд знака. Так как знаковые разряды положительных слагаемых равны нулю, разряд знака суммы тоже равен нулю. Например:

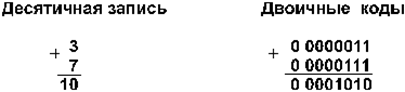
Получен правильный результат.

2. А положительное, B отрицательное и по абсолютной величине больше, чем А. Например:

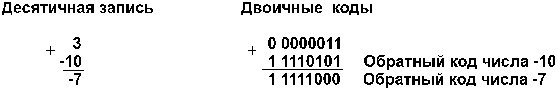
Получен правильный результат в обратном коде. При переводе в прямой код биты цифровой части результата инвертируются: 1 0000111 = –7₁₀.

3. А положительное, B отрицательное и по абсолютной величине меньше, чем А. Например:

Компьютер исправляет полученный первоначально неправильный результат (6 вместо 7) переносом единицы из знакового разряда в младший разряд суммы!!!

4. А и В отрицательные. Например:

Полученный первоначально неправильный результат (обратный код числа –11₁₀ вместо обратного кода числа –10₁₀) компьютер исправляет переносом единицы из знакового разряда в младший разряд суммы.

При переводе результата в прямой код биты цифровой части числа инвертируются: 1 0001010 = –10₁₀.

При сложении может возникнуть ситуация, когда старшие разряды результата операции не помещаются в отведенной для него области памяти. Такая ситуация называется переполнением разрядной сетки формата числа. Для обнаружения переполнения и оповещения о возникшей ошибке в компьютере используются специальные средства. Ниже приведены два возможных случая переполнения (используем калькулятор для быстрого перевода: МС – очистка памяти, МР- чтение памяти, М+ добавить в память).

5. А и В положительные, сумма А+В больше, либо равна 2^n–1, где n – количество разрядов формата чисел (для однобайтового формата n=8, 2^n–1 = 2⁷ = 128). Например:

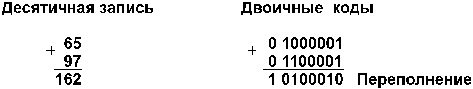
Семи разрядов цифровой части числового формата недостаточно для размещения восьмиразрядной суммы (162₁₀ = 10100010₂), поэтому старший разряд суммы оказывается в знаковом разряде. Это вызывает несовпадение знака суммы и знаков слагаемых (знак суммы – отрицателен, знак слагаемых – положительный), что является свидетельством переполнения разрядной сетки.

6. А и В отрицательные, сумма абсолютных величин А и В больше, либо равна 2^n–1.

Например:

63₂ =0111111₂

Здесь знак суммы тоже не совпадает со знаками слагаемых, что свидетельствует о переполнении разрядной сетки.

Все эти случаи имеют место и при сложении дополнительных кодов чисел:

1. А и В положительные. Здесь нет отличий от случая 1, рассмотренного для обратного кода, т.к. дополнительный код используется только для отрицательных чисел.

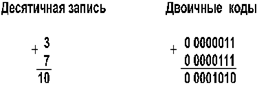
2. А положительное, B отрицательное и по абсолютной величине больше, чем А. Например:

Получен правильный результат в дополнительном коде.

При переводе в прямой код биты цифровой части результата инвертируются и к младшему разряду прибавляется единица: 1 0000110 + 1 = 1 0000111 = –7₁₀.

3. А положительное, B отрицательное и по абсолютной величине меньше, чем А. Например:

Получен правильный результат. Единицу переноса из знакового разряда компьютер отбрасывает.

4. А и В отрицательные. Например:

Получен правильный результат в дополнительном коде. Единицу переноса из знакового разряда компьютер отбрасывает.

Случаи переполнения для дополнительных кодов рассматриваются по аналогии со случаями 5 и 6 для обратных кодов.

3. Закрепление полученных знаний.

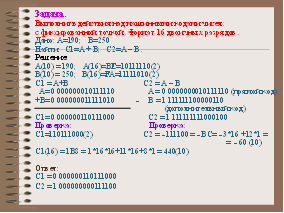
1. Какие выводы можно сделать из рассмотренных примеров кодирования чисел и арифметических действий с числами? (Оцените удобство выполнения операций).

Сравнение рассмотренных форм кодирования целых чисел со знаком показывает:

• на преобразование отрицательного числа в обратный код компьютер затрачивает меньше времени, чем на преобразование в дополнительный код, так как последнее состоит из двух шагов — образования обратного кода и прибавления единицы к его младшему разряду;
• время выполнения сложения для дополнительных кодов чисел меньше, чем для их обратных кодов, потому что в таком сложении нет переноса единицы из знакового разряда в младший разряд результата.

2. Назовите алгоритмы перевода чисел в обратный и дополнительный коды:

Алгоритм№3 (перевод числа в обратный код)

Обратный код.

1.      Записать двоичный код абсолютной величины числа.

2.      Инвертировать все цифры двоичного кода абсолютной величины числа (модуля числа), включая разряд знака: нули заменяются единицами, а единицы — нулями.

Алгоритм№4 (перевод отрицательного  числа в дополнительный код).

Дополнительный код отрицательного числа.

1.     Модуль числа записать в прямом коде в п двоичных раз­рядах. (Для этого получить внутреннее представление положительного числа N: перевести число N в двоичную систему счисления, полученный результат дополнить слева незначащими нулями до k  разрядов)

2.     Получить обратный код числа, для этого значения всех битов инвертировать (все единицы заменить на нули и все нули заменить на единицы).

3.      К полученному обратному коду прибавить единицу.

3. Назовите алгоритм перевода дополнительного кода в десятичное число

Алгоритм №5 перевода дополнительного кода в десятичное число.

1.    Инвертировать дополнительный код

2.    Прибавить к полученному коду 1 и получить модуль отрицательного числа:

3.    Перевести в десятичное число и приписать знак отрицательного числа.

4. В чем вы видите достоинства представления чисел в формате с фиксированной запятой?

Ответ: простота и наглядность представления чисел, простота алгоритмов реализации арифметических операций.                       

5.Рассмотрите пример записи дополнительного кода отрицательного числа -2002 для 16 разрядного компьютерного представления (учебник, стр. 105). В чем сущность использования дополнительного кода?

Ответ:

При n-разрядном представлении отрицательного числа в дополнительном коде старший разряд выделяется для хранения знака числа (единицы). В остальных разрядах записывается положительное число.

4. Домашнее задание:

Теория, заполнить выданные карточки.

Карточка №1

Выполнить задания по карточкам: перевести  десятичное число в двоичную систему счисления, выполнить сложение, записывая числа в прямом и дополнительном кодах.

Условие: X=A+B, где  A= -548,  B=292

Решение:

A= -548₍₁₀₎ = ____________________________________________

B=292₍₁₀₎ = ________________________________________________

Карточка №2

Выполнить задания по карточкам: перевести  десятичное число в двоичную систему счисления, выполнить сложение, записывая числа в прямом и дополнительном кодах.

Условие: X=A+B, где  A= 330,  B=-509

Решение:

A= 330₍₁₀₎ = ____________________________________________

B=-509₍₁₀₎ = ________________________________________________

Карточка №3

Выполнить задания по карточкам: перевести  десятичное число в двоичную систему счисления, выполнить сложение, записывая числа в прямом и дополнительном кодах.

Условие: X=A+B, где  A= 490,  B=-491

Решение:

A= 490₍₁₀₎ = ____________________________________________

B=-491₍₁₀₎ = ________________________________________________

Карточка №4

Выполнить задания по карточкам: перевести  десятичное число в двоичную систему счисления, выполнить сложение, записывая числа в прямом и дополнительном кодах.

Условие: X=A+B, где  A= -256,  B=-128

Решение:

A= -256₍₁₀₎ = ____________________________________________

B=-128₍₁₀₎ = ________________________________________________

Карточка №5

Выполнить задания по карточкам: перевести  десятичное число в двоичную систему счисления, выполнить сложение, записывая числа в прямом и дополнительном кодах.

Условие: X=A+B, где  A= 440,  B=-563

Решение:

A= 440₍₁₀₎ = ____________________________________________

B=-563₍₁₀₎ = ________________________________________________

Карточка №6

Выполнить задания по карточкам: перевести  десятичное число в двоичную систему счисления, выполнить сложение, записывая числа в прямом и дополнительном кодах.

Условие: X=A+B, где  A= -264,  B=-336

Решение:

A= -264₍₁₀₎ = ____________________________________________

B=-336₍₁₀₎ = ________________________________________________

Карточка №7

Выполнить задания по карточкам: перевести  десятичное число в двоичную систему счисления, выполнить сложение, записывая числа в прямом и дополнительном кодах.

Условие: X=A+B, где  A= 268,  B=-368

Решение:

A= 268₍₁₀₎ = ____________________________________________

B=-368₍₁₀₎ = ________________________________________________

Карточка №8

Выполнить задания по карточкам: перевести  десятичное число в двоичную систему счисления, выполнить сложение, записывая числа в прямом и дополнительном кодах.

Условие: X=A+B, где  A= -260,  B=-252

Решение:

A= -260₍₁₀₎ = ____________________________________________

B=-252₍₁₀₎ = ________________________________________________

Карточка №9

Выполнить задания по карточкам: перевести  десятичное число в двоичную систему счисления, выполнить сложение, записывая числа в прямом и дополнительном кодах.

Условие: X=A+B, где  A= 198,  B=-580

Решение:

A= 198₍₁₀₎ = ____________________________________________

B=-580₍₁₀₎ = ________________________________________________

Карточка №10

Выполнить задания по карточкам: перевести  десятичное число в двоичную систему счисления, выполнить сложение, записывая числа в прямом и дополнительном кодах.

Условие: X=A+B, где  A= -222,  B=-290

Решение:

A= -220₍₁₀₎ = ____________________________________________

B=-290₍₁₀₎ = ________________________________________________