Открытый урок по алгебре 9 класс. Тема: «Построение графика квадратичной функции»

Открытый урок по алгебре 9 класс.

Учитель РамазановаС.М.

Тема: «Построение графика квадратичной функции»

5.10.16г.

Цели урока:

- знать определение квадратичной функции, алгоритм построения графика квадратичной функции;

- уметь находить координаты вершины параболы, дополнительные точки, строить параболу;

- воспитывать внимательность, самостоятельность, навыки работы с чертежными принадлежностями, культуру чертежа.

Оборудование: мультимедийный проектор, индивидуальные карточки.

Ход урока.

I. Организационный момент.

На прошлом уроке мы рассмотрели различные преобразования параболы. Как вы думаете, какая цель у нас сегодня?

II. Проверка домашнего задания. (№108, 110(в, г), 111, 113). Собрать тетради.

III. Актуализация знаний. ( Фронтальный опрос. Одновременно несколько учащихся работают по индивидуальным карточкам: определить направление ветвей параболы и найти координаты вершины параболы).

1.   Функция какого вида называется квадратичной?(

2.      Что является графиком квадратичной функции? (парабола)

3.      Сколько точек необходимо для построения параболы? (минимум 5)

4.       От чего зависит направление ветвей параболы? (а>0 ветви вверх, a<0 ветви вниз)

5.   Как получается график  ?

6.      Как получается график ?

7.      Дайте название функции и скажите, что является графиком этой функции:

у = 2х -5 ,           у = 8 + 6х,             у = 2х² – 5,                у = ,       

у = -    х,         у = -3х²,                у = (х – 2)²,               у = -3(х + 1)² – 4

6. Определите, график какой функции изображен на рисунке и назовите промежутки возрастания и убывания функции, нули. 

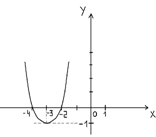
Рис. 1

А. у = - (х-3)²+ 1                 Б. у = (х+3)²-1                       В. у = (х-1)²+3

IV. Изучение нового материала.

Квадратичной функцией называется функция, которую можно задать формулой вида y=ax²+bx+c, где х - независимая переменная, a, b и с -некоторые числа (причём а≠0).

Графиком квадратичной функции является парабола, ветви которой направлены вверх(если а>0) или вниз (если а<0).

Чтобы построить график функции есть два способа:

1 способ.

1)   Выделить квадрат двучлена из квадратного трехчлена в виде  

2)       Построить график с помощью двух параллельных переносов.

2 способ.

1)      Найти координаты вершины параболы А(m;n) по формулам: ;  n = у(m) т.е. подставить найденное значение абсциссы m в формулу, которой задана функция и вычислить значение.

2)      Прямая x=m является осью симметрии параболы. 

3)      Заполнить таблицу значений функции: в таблице расположить вершину в середине таблицы и взять соседние симметричные значения х. 

4)      Построить график функции: - отметить в координатной плоскости точки, координаты которых указаны в таблице; - соединить их плавной линией. 

Построим график функции по алгоритму

у = х²-2х-1

V. Физминутка.

1. Повороты головы вправо- влево, вверх- вниз, показываем смещение вершины параболы

у =  -х²+ 3                  у =  -(х – 2)²          у =  -х²+ 6              

у = = х²- 5                  у =  (х + 1)²           у =  -х² – 8

2. Движения руками вверх- вниз, показываем направление ветвей параболы.             

у =  -х²+ 3                  у =  -(х – 2)² + 2       у =  -х²+ 6           

у = = х²- 5                  у =  (х + 1)²- 5          у =  -х² – 8

VI. Решение упражнений.

№ 121 (найти координаты вершины параболы)

№122 (построить график, выяснить свойства функции)

VII. Подведение итогов:

Ответьте на  вопросы. Верно ли, что:

1. Вершина параболы находится по формулам ….
2. При а >0 ветви параболы направлены …
3.  При а <0 ветви параболы направлены …
4. Как называют точки пересечения параболы с осью Ох?

Домашнее задание:№123, №124.