Открытый урок «Решение простейших тригонометрических уравнений»

Предмет: Алгебра и начала анализа.                                   Класс 10.

                                                                         Дата проведения – 20.12.2017 г.

Тема: «Решение простейших  тригонометрических уравнений»

Цели:

1.Образовательная: познакомить учащихся с типами тригонометрических уравнений и научить решать простейшие виды однородных, приводимых к алгебраическим и решаемых разложением на множители уравнений.

 2. Развивающая: развивать  у учащихся умение классификации предметов, поисковые навыки, учиться находить пути решения новой учебной задачи.

3.Воспитательная: воспитывать познавательную активность, самостоятельность и активность  учащихся, прививать трудолюбие.

Тип урока:  изучения нового материала

Вид урока: урок – семинар.

Форма работы: фронтальная.

Оборудование и материалы:

1.     Интерактивная доска. Презентация к уроку.

2.     Карточки-инструкции, раздаточный материал.

Ход урока

I.                  Организационный момент

II.              Актуализация опорных знаний.

1.     Назвать главные точки на тригонометрической окружности.

2.     Назвать значения тригонометрических функций для точек , находящихся в разных четвертях.

3.    Назвать точки, для которых sin t =  ,   cos t = -  ,   tg t = -1,                              ctg t = .

4.     Назвать решения частных случаев простейших тригонометрических уравнений: sin t = 0,  sin t = 1, sin t = -1,                           cos t = 0, cos t = 1, cos t = -1.

III.           Объяснение нового материала.

Перед Вами на карточках написаны три группа тригонометрических уравнений. Внимательно рассмотрите уравнения каждой группы и найдите лишние уравнения в каждой группе.

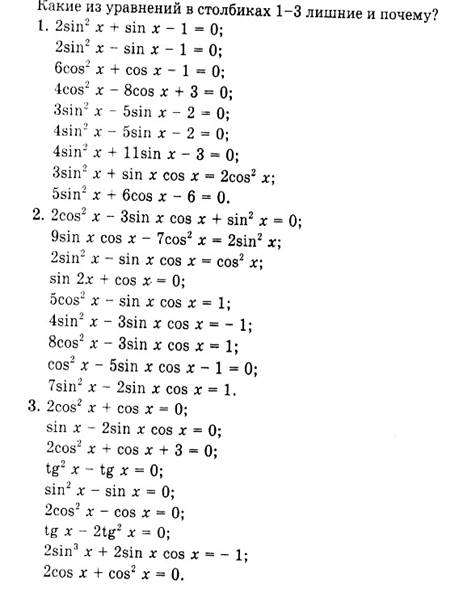
1.     Учитель знакомит учащихся с типами уравнений:  1 группа – уравнения, приводимые к алгебраическим,  2 группа - однородные  и  3 группа – уравнения, решаемые разложением на множители.

     В задачнике находим уравнения в соответствии с классификацией.

2.     Рассмотрим алгоритмы решения разных групп уравнений. Кто может предложить последовательность решения уравнений 1 группы  - уравнения, приводимые к алгебраическим.

а).Решение алгебраических уравнений заключается в том, что все тригонометрические функции, которые входят в уравнение, выражают  через какую-нибудь одну тригонометрическую функцию, зависящую от одного и того же аргумента.

Пример. 2sin² x +  sin x – 1 = 0, sin x = t,

                2t² + t – 1 =0,

                t_{1 =}  - 1 _, t_{2 =  ,}    sin x = -1 , sin x =  ,

              x ₁ = - +2πk,  , x_{2 =  +} 2πn, x_{3 =  +}2mk, k,n,m ϵZ

 Предлагаю самостоятельно решить уравнение 3 из первой группы.

6 cos²x + cos x – 1 = 0,  cos x = t,

6t² +t – 1 = 0,  D = 1 + 24 = 25, t_{1 =} -  , t₂ =

cos x = -               cos x =    

x =   + 2 πn,        x =  arccos  + 2πk, n,k ϵZ

Формулируем алгоритм решения.

  б) Решение однородных уравнений (уравнения, в которых у всех слагаемых  сумма показателей одинакова) и приводимых к ним сводится к решению алгебраических путём деления обеих частей уравнения на выражение, стоящее в левой части уравнения справа. Однородные уравнения бывают уравнениями первой степени и второй. Рассмотрим, как их определить.

        Пример.  2 cos²x – 3 cos x sinx + sin²x = 0, разделим строку на sin²x. Сделать запись. Получим уравнение 2 сtg²x – 3 ctg x + 1 = 0, приводимое к алгебраическому.

….

Чем отличается уравнение 3 sin² x –  sin x cos x = 2,

                                               3 sin² x –  sin x cos x  - 2  = 0,

                                                3 sin² x –  sin x cos x  - 2 (sin² x + cos²x)  = 0,

                                                 3 sin² x –  sin x cos x  - 2 sin² x - 2 cos²x)  = 0,

                                                        sin² x –  sin x cos x   - 2 cos² x  = 0,  разделим на cos²x,

  получим уравнение   tg²x –  tgx - 2 = 0,

……..

Формулируем алгоритм решения.

в) Решение с помощью разложения на множители сводится к решению двух элементарных уравнений.

Пример.  2cos² x – cos  x = 0, cos x ( 2 cos x – 1 ) = 0,

……

Формулируем алгоритм решения.

IV.            Подведение итогов урока: Назвать тип уравнения и способ его решения:

1.     cos x sin x + sin x = 0

2.     6 cos² x – 5 cos x sin x – sin² x = 0

3.     2 sin² x + 3 sin x + 1 = 0

V.               Домашнее задание. № 18.6, 18.11, 18.12 (а, б)