Отношения и пропорции (6 класс математика)

                            Отношения и пропорции

   Цель:

раскрыть   золотое  сечение

дать определение золотому сечению;
рассмотреть золотое сечение в окружающей среде, в искусстве и архитектуре

1. Оргмомент.

Звучит музыка.

 Здравствуйте, садитесь.  Ребята , какой сегодня прекрасный день.  Вам  желаю здоровья и плодотворной работы.  (Собачка)

 На предыдущих уроках вы познакомились с таким понятием как  «Отношения и пропорции».   1.А что такое пропорция ?

2.Что называют отношением двух чисел? (…частное двух чисел)

3. Что показывает отношение двух чисел? (…какую часть одно число составляет от другого или во сколько раз одно число больше другого).

 Мы постараемся найти общее.. Познакомимся с новыми понятиями: золотая пропорция, золотой прямоугольник, золотая спираль и еще раз убедимся в том, насколько важны математические знания в жизни людей

^ Рассмотрим новые для вас понятия.
Есть вещи, которые нельзя объяснить. Вот вы подходите к пустой скамейке и садитесь на нее. Где вы сядете - посередине? Или, может быть, с самого края?

Нет, скорее всего, не то и не другое.

Допустим длина скамейки АВ=3,25м, АС=2м, СВ= 1,25м. Найдите отношение  и .

Отношение примерно 1,6, поэтому можно составить пропорцию   = .

 Вы сядете так, что отношение одной части скамейки к другой, относительно вашего тела, будет равно примерно 1,6. Садясь на скамейку, вы произвели «золотое сечение».

Термин золотое сечение ввёл в XVI веке великий художник, учёный и изобретатель Леонардо да Винчи. В истории утвердились три варианта названия: золотое сечение, золотая пропорция и третье – деление отрезка в среднем и крайнем отношениях. Кроме того, золотое сечение награждали эпитетами «божественное», «чудесное», «превосходнейшее», потому что-то, где оно присутствует, вызывает у нас ощущение красоты и гармонии.

Чтобы и вы смогли увидеть золотое сечение в природе, в произведениях искусства, я научу вас сейчас делить отрезок в среднем и крайнем отношениях, т.е. делить отрезок в золотом отношении.    

                        D

E

                        B                                               C                                                   А

1.     Построить отрезок АВ.

2.     Построить прямой угол с вершиной в точке В.

3.     Отложить отрезок ВД=1/2 АВ.

4.     Точки А и Д соединить.

5.     Построить окружность с центром в точке Д радиусом ½ АВ.

6.     Эта окружность пересечет АД в точке Е.

7.     Построить окружность с центром в точке А радиусом АЕ.

8.     Эта окружность пересечет отрезок АВ в искомой точке С.

Золотое сечение- это деление отрезка, при котором длина большей части отрезка так относится ко всему отрезку, как длина меньшей части отрезка к большей части. Это отношение обозначим буквой φ=0,618=5/8. Говорят точка С делит отрезок АВ в «божественной пропорции».

Пифагор был первым, кто обратил внимание на особое «гармоничное» деление любого отрезка, позднее названное «золотым сечением».

Приближенные значения таковы: 1,61803398875

Итак, мы узнали , что такое золотое сечение и как разделить произвольный отрезок в золотом отношении.

У вас на столах лежит прямоугольник. Найти отношение ширины прямоугольника к его длине.

     Результаты показали, что у большинства из них отношение сторон оказалось близким к числу 0,62. И это не случайно, так как многим людям кажутся красивыми и гармоничными именно те фигуры, в которых есть элементы, связанные друг с другом золотым отношением.

Прямоугольник, стороны которого находятся в золотом отношении, т.е. отношение ширины к длине даёт число 0,62, называется золотым прямоугольником.

Окружающие нас предметы дают примеры золотого прямоугольника: обложки многих книг, журналов, тетрадей, открытки, картины, крышки столов, экраны телевизоров и т.д. близки по размерам к золотому прямоугольнику.

L                                                                                M

K                                                                                  N

Золотой прямоугольник, у которого отношение ширины к длине равно 0,618, обладает многими интересными свойствами.

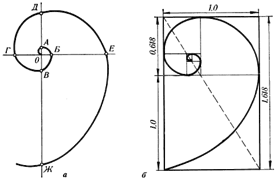
В «золотом прямоугольнике»  построим квадрат со стороной, равной меньшей стороне прямоугольника, у которого с прямоугольником общий прямой угол. Оказывается, снова получим золотой прямоугольник меньших размеров. В этом прямоугольнике снова построим квадрат, у которого с прямоугольником общий угол, и со стороной равной меньшей стороне прямоугольника. Снова получился золотой прямоугольник. Произведём несколько аналогичных построений.

Видим, что весь прямоугольник оказался составленным из вращающихся квадратов. Соединим противолежащие вершины квадратов плавной кривой. Сделаем это с помощью циркуля следующим образом…

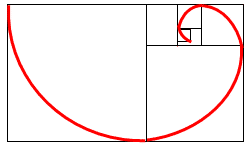
Мы получили  кривую, которая является золотой спиралью

Золотую спираль также можно заметить в созданиях природы.

По золотой спирали свёрнуты раковины многих улиток и моллюсков, некоторые пауки, сплетая паутину, закручивают нити вокруг центра по золотым спиралям. Рога архаров закручиваются по золотым спиралям.

Рассмотрим расположение семечек в корзине подсолнуха. Они выстраиваются вдоль спиралей, которые закручиваются как слева направо, так и справа налево. В одну сторону у среднего подсолнуха закручено 13 спиралей, в другую – 21 . Отношение 13/21 равно 0,62. У более крупных соцветий подсолнуха число соответствующих спиралей больше, но отношение числа спиралей, закручивающихся в разных направлениях также равно числу 0,62.

Похожее спиральное расположение наблюдается у чешуек сосновых шишек или ячеек ананаса.

  Природа повторяет свои находки, как в малом, так и в большом. По золотым спиралям закручиваются многие галактики, в частности и галактика Солнечной системы.

         Примером использования золотой спирали в живописи является например картина  Леонардо да Винчи  Портрет Моны Лизы

         Вывод :1) Мы увидели практическое применение пропорциональности в искусстве, природе. Убедились в том, что  для создания красоты необходимы знания, научные знания и в нашем случае это знание законов пропорциональности и их соблюдение.
2). Мониторинг. Определяем по цвету карточки настроение детей на конец урока.
Рефлексия

Учитель:  Вы оцените атмосферу урока, насколько интересен был для вас представленный материал. Наши оценки мы не услышим, мы их увидим. Цвет очень приятен для восприятия. Давайте остановимся на трех цветах, с которыми мы сталкиваемся ежедневно. Кстати, это очень важные цвета: красный, желтый и зеленый. Что они означают в нашей жизни?

Ориентировочный ответ учащихся: Светофор.

Учитель: У вас на столе лежат прямоугольники. Цвета прямоугольников означают следующее… (слайд). Вам осталось выбрать свой прямоугольник.

Спасибо за урок!