Относительная величина структуры

Относительная величина структуры характеризует долю отдельной части в общем объеме совокупности. Ее рассчитывают как отношение числа единиц в отдельной части совокупности к общей численности единиц (или объему) всей совокупности. Относительные величины структуры называют удельным весом или долей и исчисляют обычно в процентах ко всей совокупности либо в долях единицы.

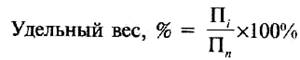
где Пi — величина отдельной части совокупности; Пn— вся совокупность (целое).

Пример. ВIV квартале у предприятия было оборотных средств на сумму 88815 тыс.руб. Из них запасы составили 47072 тыс.руб., дебиторская задолженность — 21315 тыс.руб., а денежные средства — 20428 тыс. руб. Таким образом, оборотные активы кондитерской фабрики имеют следующую структуру:

53% оборотных активов составляют запасы (47072 : 88815 х х 100%), 24% — дебиторская задолженность (21315 : 88815 х 100%) и 23% - денежные средства (20428 : 88815 х 100%).

3.      Относительные величины координации отражают соотношение между частями одного целого. К таким величинам относятся, например, соотношение между величиной заемного и собственного капитала предприятия, между численностью рабочих и административно-управленческим персоналом организации и т.д. Относительные величины координации могут показывать, сколько единиц одной части приходится на 100 или 1000 единиц другой части.

4.      Относительные величины наглядности характеризуют результат сопоставления одноименных показателей, относящихся к одному и тому же периоду времени, но к разным объектам или территориям. Эти относительные величины используются для сравнительной оценки результатов деятельности отдельных предприятий отрасли или для оценки уровня развития разных регионов. Исчисляются они либо в процентах, либо в долях единицы, показывающих, во сколько раз одна из сравниваемых величин больше (меньше) другой.

Пример. Выручка от продажи продукции кондитерской фабрики NB TV квартале была 28655 тыс.руб., что составляет 73% от среднестатистического показателя выручки от продажи аналогичной продукции в городе К.

Этот вид относительных величин нашел широкое применение в международных сопоставлениях, при сравнении результатов деятельности организаций различных форм собственности, при сопоставлении цен, величин акционерного капитала и т.д.

5.      Другой вид относительных величин — это результат сопоставления разноименных абсолютных показателей. К ним относятся относительные величины интенсивности. В их числе можно назвать такие важные коэффициенты, отражающие качественную сторону деятельности предприятия или организации, как финансовые коэффициенты деловой активности, фондоотдачу, фондовооруженность, материалоотдачу, доходность того или иного вида деятельности и пр. Эти величины исчисляются обычно в долях единицы (реже в процентах, например, рентабельность) и являются так называемыми именованными числами (т.е. имеют конкретное наименование). Важной чертой их является сопоставление разноименных абсолютных показателей. Например оборачиваемость (отдача) собственного капитала — это отношение выручки от продажи продукции (товаров) к среднегодовой стоимости собственного капитала, а рентабельность продаж — это отношение прибыли от продажи к сумме выручки, полученной от продажи продукции. В числителе и в знаменателе этих коэффициентов разноименные показатели.

Итак, относительные величины — это один из важнейших способов обобщения и анализа экономической информации. В процессе финансового анализа абсолютные и относительные величины должны рассматриваться во взаимосвязи, т.е. пользоваться относительными величинами нужно так, чтобы четко себе представлять, какая абсолютная величина стоит за каждым от-

носительным показателем. Необходимо также соблюдать сопоставимость сравниваемой величины и величины, принятой за базу сравнения.

Средняя величина является важным специальным статистическим показателем, используемым для обобщения данных. Средняя величина — это показатель «середины» или «центра» исследуемых данных. Она является обобщающей характеристикой изучаемого признака в анализируемой совокупности данных и отражает типичный уровень в расчете на единицу совокупности в конкретных условиях места и времени.

Средняя арифметическая величина определяется как отношение суммы всех значений на их количество. Средняя величина обозначается либо буквой — это сокращение от Average (средняя).

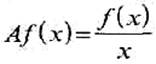
Но чаще сего средняя величина обозначается любой буквой, но обязательно с чертой наверху. Например  или

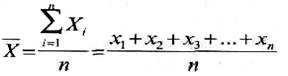
где Xj — индивидуальное значение признака каждой единицы совокупности;

п — число единиц совокупности.

При расчете средней величины мы отвлекаемся от индивидуальных особенностей отдельных составляющих частей совокупности и выражаем общие свойства, присущие всем частям совокупности. Среднее значение исключает воздействие индивидуальных причин и концентрирует закономерности, обусловленные общими причинами. Основным условием использования средней величины является качественная однородность совокупности, по которой исчислена средняя. Только при выполнении этого условия средняя величина отражает общее, типичное, закономерное, присущее всем частям анализируемой совокупности.

В анализе финансовой отчетности средние величины используются при исчислении многих показателей. Например при определении средней величины дебиторской или кредиторской задолженности предприятия в отчетном периоде для расчета срока погашения задолженности, или при определении средней величины запасов для анализа оборачиваемости материальных активов и др.

Существуют две категории средних величин: степенные средние (средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя хронологическая и др.), а также структурные средние (мода и медиана). Выбор того или иного вида средней величины зависит от цели анализа, экономической сущности усредненного показателя и характера исходных данных.

В анализе финансовой отчетности обычно используется средняя арифметическая величина (простая и взвешенная) или ее разновидность — средняя хронологическая. Наряду с этими величинами могут также исчисляться и другие виды средних.

Представим формулы вычисления различных видов средних величин, наиболее часто применяемых в практическом анализе.