Параметры. Графический способ

Параметры. Графический способ решения

Класс: 8- 9 классов

Параметр - независимая переменная, значение которой считается фиксированным или произвольным числом, или числом, принадлежащим заданному условием задачи промежутку.

Уравнение с параметром — математическое уравнение, внешний вид и решение которого зависит от значений одного или нескольких параметров.

Решить уравнение с параметром означает для каждого значения  найти значения х, удовлетворяющие этому уравнению, а также:

•         1. Исследовать, при каких значениях параметров уравнение имеет корни и сколько их при разных значениях параметров.

•         2. Найти все выражения для корней и указать для каждого из них те значения параметров, при которых это выражение действительно определяет корень уравнения.

Рассмотрим уравнение  α(х+k)= α +c, где α, c, k, x -переменные величины.

Системой допустимых значений переменных α, c, k, x называется любая система значений переменных, при которой и левая и правая части этого уравнения принимают действительные значения.

Алгоритм решения графическим методом

График функции — множество точек, у которых абсциссы являются допустимыми значениями аргумента , а ординаты — соответствующими значениями функции .

Алгоритм графического решения уравнений с параметром:

1)      Находим область определения уравнения.

2)      Выражаем α как функцию от х.

3)      В системе координат строим график функции α (х) для тех значений х, которые входят в область определения данного уравнения.

4)      Находим точки пересечения прямой α =с, с графиком функции

α (х). Если прямая α =с пересекает график α(х), то определяем абсциссы точек пересечения. Для этого достаточно решить уравнение c = α(х) относительно х.

5)      Записываем ответ

1.    Найти все значения параметра a, при которых корни уравнения 6x−5a=15 лежат на отрезке [−5;5].

Решение .

а) Перепишем исходное уравнение в виде (6х-15):5 =а, 1,2х-3=а

б) В системе координат (x; y) построим графики функций: у=1,2х -3  и у=а

в) Проведем линии х=-5 и х=5

г) Анализируя построение, можем заметить, что корни уравнения 6x−5a=15 лежат на отрезке [−5;5]   при a∈[−9;3]. (изображено синим цветом)

д) х=-5 при а=-9, х=5 при а=3

Ответ: а=-9, а=3

2.        При каких значениях р уравнение х² +3х - 2 = р имеет ровно 1 корень

Решение:

Построим графики функций в системе координат (x; y):

а) у =  х² +3х - 2  (парабола, ветви которой направлены вверх, координаты вершины параболы (-1,5; -4,25)

б) у=р — прямая, параллельная оси Ох, пересекает ось ОУ в точке с координатами (0;р)

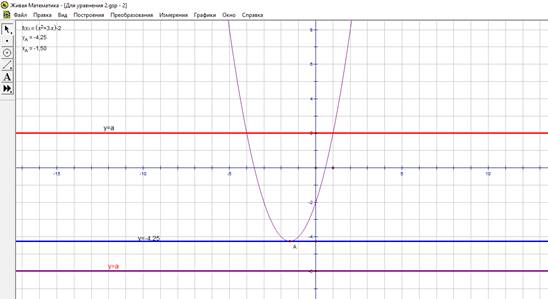
 Рассмотрим все случаи расположения графиков функций:

а) при р<4,25 графики не имеют общих точек

б) при р>-4,25 графики имеют 2 общие точки

в) при р=-4,25 графики имеют одну общую точку

Ответ: р= -4,25

3.   Сколько корней имеет уравнение | | x | – 4 | = m в зависимости от параметра m?

Решение.

а)  В системе координат (x; y) построим графики функций y = | | x | – 2 | и y = m.

б) Если 0 < m < 4, то прямая y = m имеет с графиком функции y = | | x | –4 | четыре общие точки и, следовательно, исходное уравнение имеет четыре корня.
Если m = 4, то прямая y = 4 имеет с графиком функции три общие точки. Тогда уравнение | | x | – 4 | = m  имеет три корня.
Если m > 2, то прямая y = m будет иметь с графиком исходной функции две точки, то есть данное уравнение будет иметь два корня.

Ответ: если m < 0, то корней нет;  если m = 0, m >4, то два корня;  если m = 4, то три корня; если 0 <m < 4, то четыре корня.

4.         Определить число решений уравнения +=а в зависимости от а.

Решение:

Построим графики функций:

а) у= +

при х>=3  у= 4х+2

при х  функция примет вид  у=14

при х< - 4 у=- 4х - 2

Количество решений уравнения совпадает с числом пересечения графиков функций.

Анализируя графики, получаем:

а) при а<14 графики не имеют общих точек, значит, нет решений

б) при а=14 графики пересекаются по отрезку ВС. Следовательно, уравнение имеет бесконечное число решений

в) при a>14 графики пересекаются в 2 точках. Уравнение имеет 2 решения

Ответ: при a<14 нет решений, при а=14 одно решение, при а>14 два решения

5. Постройте график функции у = -  + х - 2  и найдите значения а, при которых  прямая у = а имеет с ним ровно две общие точки.

Решение задачи:

а) Раскроем модули:  

у =  -   

Получим:  у =  -  =

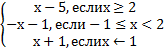
б) Построим график кусочно-непрерывной функции прямую у=а

Прямая у = аимеет с графиком данной функции ровно две общие точки

при а = -3 или  а = 0.

Ответ: при а = -3 или  а = 0

6. Сколько корней имеет уравнение x + 2 = a | x – 1 |  в зависимости от параметра a?

Решение. 

а) Заметим, что x = 1 не является корнем данного уравнения. Разделим обе части уравнения на | x – 1 |(| x – 1 | ¹ 0).

б) Уравнение примет вид =а

в) В системе координат xOy построим график функции      , при х

у=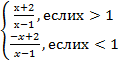        и график функции у=а

Графики изображены на рисунке. Графиком функции y = a является прямая, параллельная оси Ox или с ней совпадающая (при a = 0).

При  , графики не имеют общих точек, значит, корней нет

При -1 графики имеют одну общую точку

При а1 графики пересекаются в 2 точках

 Ответ: при  , корней нет, при -11 корень; при  а1, 2 корня

Скачано с www.znanio.ru