ПЕРЕСЕЧЕНИЯ И ОБЪЕДИНЕНИЕ

Пересечения и объединение
числовых промежутков

Цели: продолжить формирование навыков оперирования аналитической и геометрической моделями числовых промежутков; формировать умения нахождения пересечения и объединения числовых промежутков.

Ход урока

I. Организационный момент.

II. Устная работа.

1. Назовите числовой промежуток:

а)                       е) 

б)                      ж) (–3; +∞);

в)                       з) [–15; 15];

г)                       и) [5; 17);

д)                      к) (–∞; 0].

2. № 818 (в).

III. Актуализация знаний.

1. № 821, № 823 (б, в), № 824 (устно).

2. Дать определения пересечения двух множеств и объединения двух множеств.

IV. Объяснение нового материала.

Числовой отрезок – множество чисел, удовлетворяющих некоторому числовому неравенству, значит, к нему можно применить определение пересечения и объединения множеств.

Рассматриваем эти определения на конкретных примерах, причём следует охватить различные случаи взаимного расположения.

1. Найти  пересечение  и  объединение  числовых  промежутков  [1; 5]  и [3; 7].

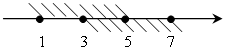
[1; 5] [3; 7] = [3; 5];

[1; 5] [3; 7] = [1; 7].

2. Найти пересечение и объединение числовых промежутков [–4; +∞) и [3; +∞).

[–4; +∞) [3; +∞) = [3; +∞);

[–4; +∞) [3; +∞) = [–4; +∞).

3. Найти  пересечение  и  объединение  числовых  промежутков  [1; 4)  и (7; +∞).

[1; 4) (7; +∞) = ;

[1; 4) (7; +∞) – не является числовым промежутком.

4. Найти пересечение и объединение промежутков (–∞; –4] и (–4; +∞).

(–∞; –4] (–4; +∞) = ;

(–∞; –4] (–4; +∞) = (–∞; +∞).

5. Найти пересечение и объединение промежутков (–∞; 0] и [0; +∞).

(–∞; 0] [0; +∞) = {0};

(–∞; 0] [0; +∞) = (–∞; +∞).

V. Формирование умений и навыков.

1. № 825.

Р е ш е н и е

а) 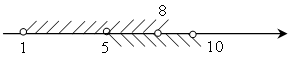           (1; 8) (5; 10) = (5; 8);

б)             [–4; 4] [–6; 6] = [–4; 4];

в) 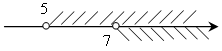                 (5; +∞) (7; +∞) = (7; +∞);

г)                   (–∞; 6) (–∞; 10) = (–∞; 6).

2. № 826.

Р е ш е н и е

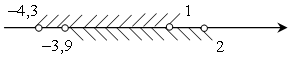
(–4,3; 1) (–3,9; 2) = (–3,9; 1).

В полученный интервал входят целые числа:

–3; –2; –1; 0.

О т в е т: четыре числа.

3. № 827.

Р е ш е н и е

а)               [–7; 0] [–3; 5] = [–7; 5];

б)          (–4; 1) (10; 12);

в)           (–∞;4) (10; +∞);

г)            [3; +∞) (8; +∞) = [3; +∞).

VI. Самостоятельная работа.

1. Заполнить таблицу по образцу.

Окончание табл.

2. Сильным в учебе учащимся можно предложить задание повышенной трудности.

№ 820.

Р е ш е н и е

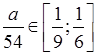, то есть 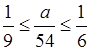. Домножим неравенство на 54, получим 6 ≤ а ≤ 9. Так как а N, то а принадлежит множеству {6; 7; 8; 9}. Значит, промежутку 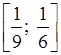 принадлежат дроби .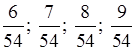

О т в е т: .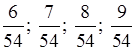

VII. Итоги урока.

В о п р о с ы   у ч а щ и м с я:

– Как изобразить на координатной прямой пересечение числовых промежутков? Объединение числовых промежутков?

– Всегда ли пересечение (объединение) числовых промежутков есть числовой промежуток? Приведите примеры.

Домашнее задание: № 822, № 823 (а, г), № 828, № 936.