ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ В
ПРОСТРАНСТВЕ.
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ, ПЕРПЕНДИКУЛЯРНЫЕ
К ПЛОСКОСТИ
Цели: доказать лемму о перпендикулярности двух параллельных прямых к третьей прямой; дать определение прямой, перпендикулярной к плоскости.
Ход урока
I. Повторение пройденного материала.
Актуализация знаний.
Цель – повторить, как определяется угол между прямыми в пространстве.
|
|
Дано: ABCDA1B1C1D1
– параллелепипед. Найдите угол между прямыми АВ и А1D1; А1В1 и AD; АВ и В1С1.
|
BAD = 30°.
Докажите,
что ВС 
B1C1
и AB 
A1D1.
АDD1 = 90°.
Докажите,
что AB 
CC1и DD1
A1B1.
II. Объяснение нового материала.
Рассмотрим модель куба. Как называются прямые АВ и ВС? Какие прямые называются перпендикулярными? Найдите угол между прямыми АА1 и DC; ВВ1 и AD. Эти прямые тоже перпендикулярные. В пространстве перпендикулярные прямые могут пересекаться и могут быть скрещивающимися.
|
|
Рассмотрим прямые АА1, СС1 и DC. Прямая АА1 параллельна прямой СС1, а прямая СС1 перпендикулярна прямой CD. Нами установлено, что АА1 перпендикулярна CD. Сформулируйте это утверждение. |
Формулируется и доказывается лемма.
III. Решение задач.
№ 117.
|
|
Рассмотрим модель куба. Найдите
угол между прямой АА1 и прямыми плоскости Вывод: прямая АА1 перпендикулярна любой прямой, лежащей в плоскости (АВС). Такие прямая и плоскость называются перпендикулярными. |
Дайте четкое определение прямой, перпендикулярной к плоскости. Докажите, что если прямая а перпендикулярна к плоскости α, то она пересекает эту плоскость (см. п. 16).
Доказать две теоремы, в которых устанавливается связь между параллельностью прямых и их перпендикулярностью к плоскости.
№ 120.
|
|
Дано: ABCD – квадрат, АВ = а, АС Найдите: АK, ВK, СK, DK. 1. Доказать, что АK = ВK = СK = DK. |
BD = О, ОK
(АВС),
ОK = b.2. AK =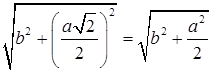
.
Домашнее задание. Теория (п. 15, 16). №№ 118, 121. (Указание: медиана, проведенная в прямоугольном треугольнике к гипотенузе, равна ее половине.)
ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ В ПРОСТРАНСТВЕ
© ООО «Знанио»
С вами с 2009 года.
