ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ

ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА
ТРЕУГОЛЬНИКОВ

Цели: выработать у учащихся умение применять при решении задач изученные свойства и теорему о равенстве треугольников по двум сторонам и углу между ними; развивать логическое мышление учащихся.

Ход урока:

I. Проверка усвоения изученного материала.

1. Проверить знание первого признака равенства треугольников
(один человек – у доски и можно три человека с листочками – за первыми партами).

2. Два человека у доски записывают решение домашних задач № 94 и 95.

3. Устная работа с классом:

1) Контрольные вопросы 1–4 на с. 49–50.

2) Решение задач по готовым чертежам:

а) Какие треугольники равны на рисунке 1 и почему?

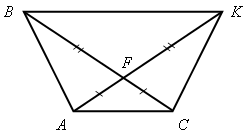
Рис. 1

б) На рисунке 2 в треугольниках АВD и АСD.

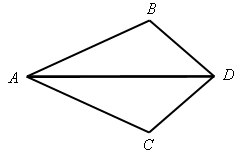
Рис. 2

ВАD = САD; АВ = АС.

Найдите периметр АВD, если АС = 5 см, СD = 3 см, АD больше АС на 2 см.

в) МNO = МRO (рис. 3). Доказать, что NOР = ROР.

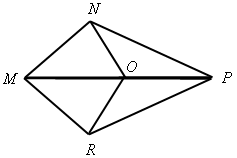
Рис. 3

II. Решение задач.

При построении чертежей обязательно использовать цветные мелки.

1. Решить задачу № 98 (решение объясняет учитель, привлекая учащихся).

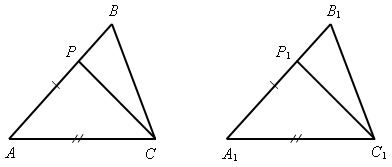
Дано: АСВ и А₁С₁В₁; АВ = А₁В₁; АС = А₁С₁;

А = А₁; АР = А₁Р₁.

Доказать: ВРС = В₁Р₁С₁.

Доказательство

Рассмотрим АСВ и А₁С₁В₁:

АВ = А₁В₁ (по условию), АС = А₁С₁ (по условию), А = А₁ (по условию), тогда АСВ = А₁С₁В₁ (первый признак, равны по двум сторонам и углу между ними).

Отсюда ВС = В₁С₁ и В и В₁.

По условию АВ = А₁В₁ и АР = А₁Р₁, то РВ = Р₁В₁.

Рассмотрим ВРС и В₁Р₁С₁:

2. Решить задачу № 99 на доске и в тетрадях.

III. Самостоятельная работа (10 минут).

Вариант I

Вариант II

Докажите равенство треугольников АВС и АDС, изображенных на рисунке 53 учебника, если АВ = DС и 4 = 3. Найдите углы АСВ и АDС, если АВС = 102°, ВСА = 38°.

Вариант III
(для более подготовленных учащихся)

Известно, что АВС и А₁В₁С₁ равны, причем А = А₁, В = В₁.

На сторонах АС и А₁С₁ отмечены точки D и D₁ так, что СD = С₁D₁.

Докажите, что СВD = С₁В₁D₁.

Вариант IV
(для более подготовленных учащихся)

Известно, что треугольник MKP равен треугольнику М₁K₁Р₁, причем М = М₁, K = K₁. На сторонах МР и М₁Р₁ отмечены точки Е и Е₁ так, что МЕ = М₁Е₁.

Докажите, что МЕK = М₁Е₁K₁.

IV. Итоги урока.

Домашнее задание: повторить пункты 14, 15; ответить на вопросы 1–4 на с. 49–50; решить задачи №№ 97, 160(а).