PHY_10_14_V1_TG_Practical applications of electromagnetic fields

Teacher Guides of the Lesson

Theoretical material for the lesson, definitions for concepts 

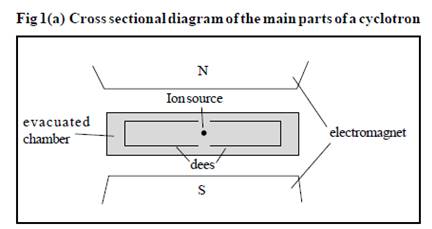
The Cyclotron

The cyclotron consists of:

·         An evacuated chamber to minimize energy losses resulting from collisions of ions with air molecules.

·         A source of charged particles that are to be accelerated – an ion source.

·         Two ‘dees’ across which an alternating voltage is applied that accelerates the ions when they move from one dee to the next.

·         A uniform magnetic field that keeps the ions moving in a circular path and confines them to the two dees. This magnetic field is usually produced by an electromagnet.

A cyclotron can be used to accelerate positively or negatively charged ions.

In the following explanation the ions are considered to be positive ions.

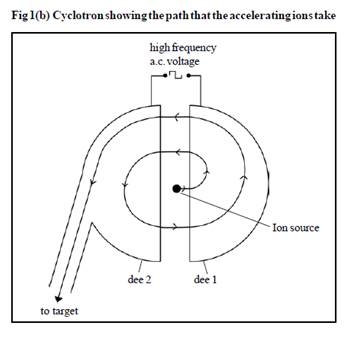
• Positive ions are released from the ion source. These positive ions are accelerated towards dee 1, which is initially given a negative potential to attract the positive ions.

• Once inside dee 1 the positive ions move at constant speed. A uniform magnetic field is applied perpendicularly to the dees by the electromagnet.

This magnetic field makes the positive ions move in a circular path.

• The positive ions turn around and move towards the gap from dee 1 into dee 2.

• The alternating voltage reverses giving dee 2 a negative potential. When the positive ions cross the gap from dee 1 into dee 2 they are accelerated towards dee 2 by the negative potential.

Once inside dee 2 the positive ions have a faster speed than when they were in dee 1 - this remains constant within the dee. The above sequence of events now repeats itself. The magnetic field makes the ions move in a semi-circle back to the gap between the dees at which point the alternating voltage has reversed and so the positive ions are accelerated back across the gap towards

dee1, which now has a negative potential once more. As the speed increases, the radius of the circular path followed by the ions

increases but the time that the ion spends in each dee remains constant. This means that the frequency of the alternating voltage remains constant.

The path of the ions

1. The constant magnetic field applied perpendicular to the dees exerts

a force on the ions that makes them move in a circular path.

2. The speed inside a dee remains constant.

3. The speed of the ions increases as they move from one dee to the next.

This is because they are attracted to the oppositely charge dee.

4. The ions spend an equal amount of time in each dee, as they speed

up, the circular path increases in radius and they travel further in

each dee.

Exam Hint: Questions that require explanation type answers are best

presented as ‘bullet points’ as shown in the explanations given about the

cyclotron accelerator. They help you to order your thoughts and make

it easier for the examiner to identify the important points that deserve a

mark. All bullet points should remain as structured sentences as marks

are also awarded on exam papers for your ‘quality of written

communication.’

A closer look at the speed attained by accelerated particles

We will now derive an expression for the speed of the ions inside the cyclotron by applying Newton’s second law of motion, but before we do this we need to know the following:

The force exerted on a charged particle moving perpendicular through a magnetic field acts as a centripetal force, moving the particle in a circular path.

The size of this force is:

F = Bqv B = size of magnetic field (T)

q = charge on particle (C)

v = speed of particle (m/s)

The acceleration of an object moving in a circle is given by the expression:

a = v²/r,  v = speed of object (m/s)

r = radius of circular path of the object (m)

We are now in a position to use Newton’s second law on the ions in the cyclotron that are moving in a circle:

F = ma where : m = mass of ion (kg)

Substituting into this equation the expressions for centripetal force and

acceleration that are stated above we get:

Bqv =mv²/r

Rearranging this to make speed, v, the subject of the equation:

v =Bqr/m

For any particular ion, its charge, q, and its mass, m, will remain constant. This equation also shows that if the magnetic field strength is constant, the speed of the particle is proportional to the radius of its circular path. As the ions move from dee to dee, their speed increases. This means that the ions move in larger and larger circles as they accelerate up to the radius of

the dees themselves, at which point they cannot be accelerated anymore and they are released towards the target.

The maximum speed of the particles.

For any particular ion, the maximum speed that it can reach is

limited by two factors:

1. The radius of the cyclotron

2. The maximum magnetic field strength that can be applied.

Limitations of a cyclotron

As particles approach very high speeds, close to the speed of light, their mass increases. This effect is predicted by special relativity. This means that the particles spend slightly longer in each dee. This means that the alternating voltage reverses too soon for the particles to be accelerated across the gap.

The synchronisation of the voltage and the ions is lost. This happens at energies of about 20 MeV, meaning that a more sophisticated particle accelerator is needed for higher energies.

Exam Hint: Be very careful when an answer requires you to use a value that you have previously calculated in the question. You must always carry forward as many significant figures as possible when using a calculated value in a subsequent part of the question. This is despite

having to round these previous values up before quoting them as an answer.

Instructions for demonstrations and safety

Warning: experiments with electricity should be performed under the supervision of teachers or adults familiar with electricity safety procedures.

Additional guidelines for organizing a lesson 

1.      Organization moment. Establishing emotional state. Checking for absent students.

2.      Teacher introduces the topic and objectives of the lesson, assess criteria.

3.      As a starter of the lesson, ask learners name the apparatus on presentation by using whiteboard. Each student should write with markers on the whiteboard and raise it. 

4.      Teacher suggests that learners individually to do Concept and Calculation Test involving calculation with use of the formulae of circular motion of charged particles in a cyclotron. Concept Test answers can be found in the text which teacher provides each student.

5.       Pairs assess each other’s work and provide fair and helpful feedback by using an answer   sheet.

6.      At the end of the lesson students are encouraged to reflect on what they have learned and

               what they need to improve.

Recommendations for formative assessment

Activity1. Students discuss learning objectives and assess criteria.

Activity2. (WHITEBOARD – name it!) Learners name the apparatus on presentation by using

                 whiteboard. Each student should write with markers on the whiteboard and raise it.  Activity3. Learners individually do Concept and Calculation Test involving calculation with

                 use of the formulae of circular motion of charged particles in a cyclotron. Concept

                 Test answers can be found in the text which teacher provides each student.

Activity4. Pairs assess each other’s work and provide fair and helpful feedback by using an

                 answer sheet.

Activity5. At the end of the lesson students are encouraged to reflect on what they have learned

       and what they need to improve.

Answers, criteria for assignments, additional materials for the lesson

Activity 5

Answer

Quantitative Test Answers

1. (a) Energy = qV = (1.6 × 10^-19)(1500) = 2.4 × 10^-16 J

(b) Kinetic Energy = Energy gained

½mv² = 2.4 × 10^-16

v² = 2 × (2.4 × 10^-16)/1.7 × 10^-27 = 2.8 × 10¹¹

v = √(2.8 x 10¹¹) = 5.3 x 10⁵ m/s

2. (a) r = mv/ Bq = (9.11 × 10^-31)(2 × 10⁷)/ 0.1 × (1.6 × 10^-19) = 1.1 × 10^-3 m = 1.1mm

(b) speed = distance/time

time = distance / speed = (½ × circumference)/ speed

speed speed = (½)(2π)(1.1 × 10^-3) / (2 × 10⁷)  = 1.8 × 10^-10 s

List of useful links and literature 

Douglas C. Giancoli, Physics Principles with Applications, Seventh edition  2014.

David Sang, Graham Jones, Gurinder Chadha and Richard Woodside, Cambridge International    

AS and A Level Physics Coursebook Second Edition, 2014

 https://opentextbc.ca/physicstestbook2/chapter/force-on-a-moving-charge-in-a-magnetic-field-       

examples- and-applications/

Скачано с www.znanio.ru