PHY_10_15_V1_TG_The law of universal gravitation

TEORETICAL MATERIALS FOR LESSON

Defining Graviational Potential Energy

Gravitational energy is the potential energy associated with gravitational force, such as elevating objects against the Earth’s gravity.

LEARNING OBJECTIVES

Express gravitational potential energy for two masses

KEY TAKEAWAYS

KeyPoints

·         If an object falls from one point to another point inside a gravitational field, the force of gravity will do positive work on the object, and the gravitational potential energy will decrease by the same amount.

·         Near the surface of the Earth, the work done in lifting an object through a height h is the product mgh, so U=mgh

·         The gravitational potential energy, U, of a system of masses m₁ and M₂ at a distance r using gravitational constant G is U=−Gm₁M₂/r

KeyTerms

·         Newton’s law of gravitation: This law states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.

·         potential energy: The energy an object has because of its position (in a gravitational or electric field) or its condition (as a stretched or compressed spring, as a chemical reactant, or by having rest mass)

·         gravity: Resultant force on Earth’s surface, of the attraction by the Earth’s masses, and the centrifugal pseudo-force caused by the Earth’s rotation.

Gravitational energy is the potential energy associated with gravitational force, as work is required to elevate objects against Earth’s gravity. The potential energy due to elevated positions is called gravitational potential energy, and is evidenced by water in an elevated reservoir or kept behind a dam. If an object falls from one point to another point inside a gravitational field, the force of gravity will do positive work on the object, and the gravitational potential energy will decrease by the same amount.

Consider a book placed on top of a table. As the book is raised from the floor to the table, some external force works against the gravitational force. If the book falls back to the floor, the “falling” energy the book receives is provided by the gravitational force. Thus, if the book falls off the table, this potential energy goes to accelerate the mass of the book and is converted into kinetic energy. When the book hits the floor, this kinetic energy is converted into heat and sound by the impact.

The factors that affect an object’s gravitational potential energy are its height relative to some reference point, its mass, and the strength of the gravitational field it is in. Thus, a book lying on a table has less gravitational potential energy than the same book on top of a taller cupboard, and less gravitational potential energy than a heavier book lying on the same table. An object at a certain height above the Moon’s surface has less gravitational potential energy than at the same height above the Earth’s surface because the Moon’s gravity is weaker. Note that “height” in the common sense of the term cannot be used for gravitational potential energy calculations when gravity is not assumed to be a constant. The following sections provide more detail.

Local Approximation

The strength of a gravitational field varies with location. However, when the change of distance is small in relation to the distances from the center of the source of the gravitational field, this variation in field strength is negligible and we can assume that the force of gravity on a particular object is constant. Near the surface of the Earth, for example, we assume that the acceleration due to gravity is a constant g=9.8m/s² (“standard gravity”). In this case, a simple expression for gravitational potential energy can be derived using the W=Fd equation for work. The upward force required while moving at a constant velocity is equal to the weight, mg, of an object, so the work done in lifting it through a height h is the product mgh. Thus, when accounting only for mass, gravity, and altitude, the equation is:

U=mgh

where U is the potential energy of the object relative to its being on the Earth’s surface, mm is the mass of the object, g is the acceleration due to gravity, and h is the altitude of the object. If m is expressed in kilograms, g in m/s² and h in meters then U will be calculated in joules. In most situations, the change in potential energy is the relevant quantity:

ΔU=mgΔh

General Formula

However, over large variations in distance, the approximation that gg is constant is no longer valid, and we have to use calculus and the general mathematical definition of work to determine gravitational potential energy. For the computation of the potential energy, we can integrate the gravitational force, whose magnitude is given by Newton’s law of gravitation, with respect to the distance r between the two bodies. Using that definition, the gravitational potential energy of a system of masses m₁ and M₂ at a distance rr using gravitational constant G is

U=−Gm₁M₂/r+K

where K is the constant of integration. Choosing the convention that K=0 makes calculations simpler, albeit at the cost of making Unegative. Note that in this case the potential energy becomes zero when r is infinite, and approaches negative infinity as rr goes to zero.

Trebuchet: A trebuchet uses the gravitational potential energy of the counterweight to throw projectiles over long distances.

Energy Conservation

Escape Speed

An object reaches escape speed when the sum of its kinetic energy and its gravitational potential energy is equal to zero.

LEARNING OBJECTIVES

Calculate the escape speed of an object given its kinetic energy and the gravitational potential energy

KEY TAKEAWAYS

KeyPoints

·         It is assumed that the velocity of the object at the ending point will be zero.

·         The requisite escape speed (se) of an object to escape a spherically symmetric body is given by: se=√2GMr, where G is the universal gravitational constant, M is the mass of the body, and r is the distance of the object from the body’s center of gravity.

·         Escape speed is the required speed that an object has to have to go from a starting point in a gravitational potential field to an ending point that is infinitely far away.

·         The speed at which a body rotates will affect the required velocity that an object must have relative to the surface of the body.

·         Objects that have propulsion systems do not need to reach escape velocity.

KeyTerms

·         propulsion: Forcecausingmovement.

·         potential energy: The energy an object has because of its position (in a gravitational or electric field) or its condition (as a stretched or compressed spring, as a chemical reactant, or by having rest mass)

·         kinetic energy: The energy possessed by an object because of its motion, equal to one half the mass of the body times the square of its velocity.

Escape speed is the required starting speed required by an object to go from a starting point in a gravitational potential field to an ending point that is infinitely far away. It is assumed that the velocity of the object at the ending point will be zero.

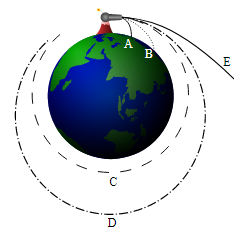
Isaac Newton’s Analysis of Escape Speed: In this figure, Objects A and B don’t have the required escape speed and so they fall back to Earth after launch. Objects C and D don’t either, they achieve a circular and an elliptical orbit respectively. Object E is launched with sufficient escape velocity and escapes the Earth.

Imagine a situation in which a spaceship that does not have a propulsion system is launched straight away from a planet. (It is moot to discuss escape speed for objects with propulsion systems.) Let us assume that the only significant force that is acting on the spaceship is the force of gravity from the planet. The escape speed of the spaceship can calculated through a simple analysis of conservation of energy. The gravitational potential energy of the spaceship is:

U=−GMm/r

Where G is the universal gravitational constant (G=6.67⋅10⁻¹¹ m³kg⁻¹s⁻²), M is the mass of the planet, m is the mass of the spaceship, and r is the distance of the spaceship from the planet’s center of gravity.

At the ending point of the spaceship, r goes to infinity. As r goes to infinity, the value of the gravitational potential energy expression goes to 0.

The kinetic energy of the spaceship can be found from:

mv²

Where mm is the mass of the spaceship and v is the velocity of the spaceship.

At the starting point of the spaceship, the velocity must have a magnitude equal to the escape speed (s_e). The velocity of the spaceship is 0 at its ending point, and so consequently its kinetic energy is 0 in the end as well.

Summarizing the kinetic energy (K) and potential energy (U) of the spaceship at it’s initial (i) and final (f) states:

(K+U)_i=ms_e²+−GMm/r

(K+U)_f=0+0

Due to conservation of energy, the initial energy must equal the final energy and so we can solve for s_e:

s_e=√2GMr

Interestingly, if the spaceship were to fall to the planet from a point infinitely far away it would obtain a final speed of se at the planet.

It should be noted that if an object is launched from a rotating body, such as the Earth, the speed at which the body rotates will affect the required velocity that an object must have relative to the surface of the body. If a rocket is launched tangentially from the Earth’s equator in the same direction that the Earth is turning, it will require a lower velocity relative to the Earth than if it were launched in the opposite direction to meet escape speed requirements.

Additionally, it is a misconception that powered vehicles (such as rockets) require escape speed to leave orbit and travel through outer-space. If the vehicle has a propulsion system to provide it with energy once it has left the surface of the planet, it is not necessary to initially meet escape speed requirements.

List of useful links

https://www.britannica.com/science/Newtons-law-of-gravitation

https://courses.lumenlearning.com/boundless-physics/chapter/energy-conservation/

https://www.physicsclassroom.com/class/circles/Lesson-3/Newton-s-Law-of-Universal-Gravitation

http://alexandr4784.narod.ru/lewantov.htm

http://studopedia.ru/2_124334_orbitalnoe-dvizhenie.html

http://lib4all.ru/base/B2005/B2005Part61-171.php

http://kvant.mccme.ru/1989/04/orbitalnoe_dvizhenie.htm

http://docplayer.ru/422607-Mehanika-kosmicheskogo-poleta-orbitalnoe-

dvizhenie.html

http://www.physbook.ru/index.php/Kvant._%D0%9E%D1%80%D0%B1%D0%B8%

D1%82%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5_%D0%B4%D

0%B2%D0%B8%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5

7.  Видео лекция: ИСЗ. 1-я космическая скорость. Геостационарная Орбита.

https://www.youtube.com/watch?v=xQOns-yfmJI

https://ru.wikipedia.org/wiki/%D0%93%D0%B5%D0%BE%D1%81%D0%B8%D0

%BD%D1%85%D1%80%D0%BE%D0%BD%D0%BD%D0%B0%D1%8F_%D0%

BE%D1%80%D0%B1%D0%B8%D1%82%D0%B0

http://dic.academic.ru/dic.nsf/ruwiki/68406

http://www.sat.belastro.net/glava2/glava2.php

http://www.kosmofizika.ru/spravka/geosynch.htm

http://unnatural.ru/earth-orbits-2

http://www.linux.org.ru/forum/talks/7995739

https://www.youtube.com/watch?v=SBlmnmS0Jv8

 https://www.youtube.com/results?search_query=%D0%B2%D0%B8%D0%B4+%D0

%B7%D0%B5%D0%BC%D0%BB%D0%B8+%D1%81+%D0%BC%D0%BA%D1

%81

https://www.youtube.com/watch?v=8GzKxnMOvDw

https://www.youtube.com/watch?v=l3f53oMuDBc

Скачано с www.znanio.ru