PHY_10_16_V1_DM_Moment of inertia of a perfectly rigid body

Differentiated problems

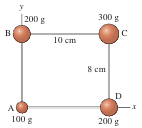
1. ||  The four masses shown in Figure 1 are connected by massless, rigid rods.

a.  Find the coordinates of the center of mass.

b.  Find the moment of inertia about an axis that passes through mass A and is perpendicular to the page.

2. ||  The four masses shown in Figure 1 are connected by massless, rigid rods.

a.  Find the coordinates of the center of mass.

b.  Find the moment of inertia about a diagonal axis that passes through masses B and D.

3.  |  The three masses shown in Figure eX12.15 are connected by massless, rigid rods.

a.  Find the coordinates of the center of mass.

b.  Find the moment of inertia about an axis that passes through mass A and is perpendicular to the page.

c.  Find the moment of inertia about an axis that passes through masses B and C.

4. ||  A 12-cm-diameter CD has a mass of 21 g. What is the CD’s moment of inertia for rotation about a perpendicular axis (a) through its center and (b) through the edge of the disk?

5.  ||  A 25 kg solid door is 220 cm tall, 91 cm wide. What is the door’s moment of inertia for (a) rotation on its hinges and (b) rotation about a vertical axis inside the door, 15 cm from one edge?

Solution of the problems

1.  Model:  The moment of inertia of any object depends on the axis of rotation. In the present case, the rotation axis passes through mass A and is perpendicular to the page.

Solve:  (a)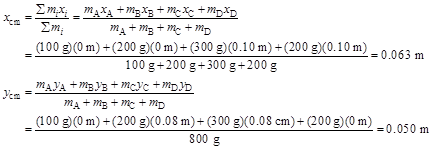

(b)The distance from the axis to mass C is 12.81 cm. The moment of inertia through A and perpendicular to the page is

2.  Model:  The moment of inertia of any object depends on the axis of rotation.

Visualize:  

Solve:  (a)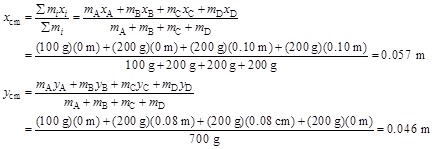

(b) The moment of inertia about a diagonal that passes through B and D is

where we must compute  which are the distances from the diagonal. From triangle ABD we see that  Now   Thus,

Assess:  Note that the masses B and D, being on the axis of rotation, do not contribute to the moment of inertia.

3.  Model:  The three masses connected by massless rigid rods are a rigid body.

Solve:  (a)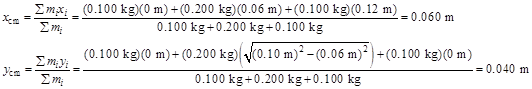

(b) The moment of inertia about an axis through A and perpendicular to the page is

(c) The moment of inertia about an axis that passes through B and C is

Assess:  Note that mass  does not contribute to  and the masses  and  do not contribute to

4.  Model:  The CD is a disk of uniform density.

Solve:  (a) The center of the CD is its center of mass. Using Table 12.2,

(b) Using the parallel–axis theorem with

5.  Model:  The door is a slab of uniform density.

Solve:  (a) The hinges are at the edge of the door, so from Table 12.2,

(b) The distance from the axis through the center of mass along the height of the door is Using the parallel–axis theorem,

Assess:  The moment of inertia is less for a parallel axis through a point closer to the center of mass.

Conceptual questions

1.      Is the center of mass of the dumbbell in Figure  3 at point a, b, or c? Explain.

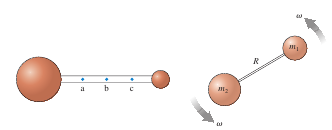
2.  If the angular velocity v is held constant, by what factor must R

change to double the rotational kinetic energy of the dumbbell in Figure 2

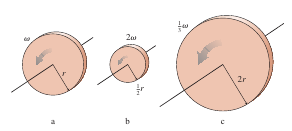
3.  Figure 3 shows three rotating disks, all of equal mass. Rank in order, from largest to smallest, their rotational kinetic energies Ka to Kc.

4.  Must an object be rotating to have a moment of inertia? Explain.

5.  The moment of inertia of a uniform rod about an axis through its center is 1/12 mL². The moment of inertia about an axis at one end  is 1/3 mL². Explain why the moment of inertia is larger about the end than about the center.

6.  You have two solid steel spheres. Sphere 2 has twice the radius of sphere 1. By what factor does the moment of inertia I₂ of sphere 2 exceed the moment of inertia I₁ of sphere 1?

7.  The professor hands you two spheres. They have the same mass, the same radius, and the same exterior surface. The professor claims that one is a solid sphere and the other is hollow. Can you determine which is which without cutting them open? If so, how? If not, why not?

Answers to the conceptual questions

1.  As suggested by the figure, we will assume that the larger sphere is more massive. Then the center of gravity would be at point a because if we suspend the dumbbell from point a then the counterclockwise torque due to the large sphere (large weight times small lever arm) will be equal to the clockwise torque due to the small sphere (small weight times large lever arm).

Look at the figure and mentally balance the dumbbell on your finger; your finger would have to be at point a. The sun-earth system is similar to this except that the sun’s mass is so much greater than the earth’s that the center of mass (called the barycenter for astronomical objects orbiting each other) is only 450 km from the center of the sun.

2.  To double the rotational energy without changing  requires doubling the moment of inertia. The moment of inertia is proportional to  so R must increase by

3.  The rotational kinetic energy is For a disk,  Since the mass is the same for all three disks, the quantity  determines the ranking. Thus

4.  No. The moment of inertia does not have any dependence on a quantity that indicates an object is rotating, such as  or  so an object does not have to be rotating to have a moment of inertia.

5.  Mass that is farther away from the axis of rotation contributes more to the moment of inertia Here, r is the distance from the axis of rotation to the mass element dm. Note  is always positive. For a rod, there is more mass farther away from an axis through the rod’s end than one through its middle.

6.  Because sphere 2 has twice the radius, its mass is greater by a factor of The added mass is also distributed farther from the center, so,  leads to

7.  It will be easier to rotate the solid sphere because the hollow sphere’s mass is generally distributed farther from its center. If you roll both simultaneously down an incline, the solid sphere will win.