PHY_10_16_V1_TG_Moment of inertia of a perfectly rigid body

Moment of inertia

Mass moment of inertia for a particle: The mass moment of inertia is one measure of the distribution of the mass of an object relative to a given axis. The mass moment of inertia is denoted by I and is given for a single particle of mass m as

where O-O is the axis around which one is evaluating the mass moment of inertia, and r is the perpendicular distance between the mass and the axis O-O. As can be seen from the above equation, the mass moment of inertia has the units of mass times length squared. The mass moment of inertial should not be confused with the area moment of inertia which has units of length to the power four. Mass moments of inertia naturally appear in the equations of motion, and provide information on how difficult (how much inertia there is) it is rotate the particle around given axis.

Mass moment of inertia for a rigid body: When calculating the mass moment of inertia for a rigid body, one thinks of the body as a sum of particles, each having a mass of dm. Integration is used to sum the moment of inertia of each dm to get the mass moment of inertia of body. The equation for the mass moment of inertia of the rigid body is

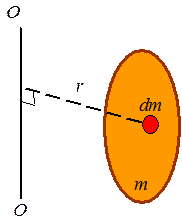
The integration over mass can be replaced by integration over volume, area, or length. For a fully three dimensional body using the density  one can relate the element of mass to the element of volume. In this case the density has units of mass per length cubed and the relation is given as

and the equation for the mass moment of inertia becomes

The integral is actually a triple integral. If the coordinate system used is rectangular then dV=dxdydz . If the coordinates uses are cylindrical coordinates then .

For a two dimensional body like a plate or a shell one can use density   per unit area (units of mass per length squared) to change the integration using the relation

where A is the surface are and dA differential element of area. For example, for rectangular coordinates dA=dxdy and for polar coordinates . After this substitution one gets the equation to calculate the mass moment of inertia as

If the body is a rod like object then one can use the relation

to get

where l is a coordinate along the length of the rod  and the density  is in units of mass per unit length.

Radius of gyration: Sometime in place of the mass moment of inertia the radius of gyration k is provided. The mass moment of inertia can be calculated from k using the relation

where m is the total mass of the body. One can interpret the radius of gyration as the distance from the axis that one could put a single particle of mass m equal to the mass of the rigid body and have this particle have the same mass moment of inertia as the original body.

Parallel-axis theorem: The moment of inertia around any axis can be calculated from the moment of inertia around parallel axis which passes through the center of mass. The equation to calculate this is called the parallel axis theorem and is given as

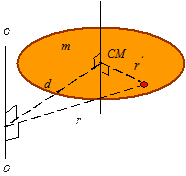
where d is the distance between the original axis and the axis passing through the center of mass, m is the total mass of the body, and  is the moment of inertia around the axis passing through the center of mass.

Composite bodies: If a body is composed of several bodies, to calculate the moment of inertia about a given axis one can simply calculate the moment of inertia of each part around the given axis and then add them to get the mass moment of inertia of the total body.

Problem for differentiation

‘Low inertia’ motors are used in applications requiring rapid changes of speed and direction of rotation. These motors are designed so that the rotor has a very low moment of inertia about its axis of rotation.

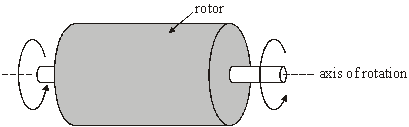
(a)     (i)      Explain why a low moment of inertia is desirable when the speed and direction of rotation must be changed quickly.

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

(ii)     State, giving a reason in each case, two features of rotor design which would lead to a low moment of inertia about the axis of rotation.

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

(4)

(b)     In one application, a rotor of moment of inertia 4.4 × 10^–5 kg m² about its axis of rotation is required to reverse direction from an angular speed of 120 rad s^–1 to the same speed in the opposite direction in a time of 50 ms. Assuming that the torque acting is constant throughout the change, calculate

(i)      the angular acceleration of the rotor,

____________________________________________________________________________________________________________________________

(ii)     the torque needed to achieve this acceleration,

____________________________________________________________________________________________________________________________

(iii)     the angular impulse given to the rotor during the time the torque is acting,

____________________________________________________________________________________________________________________________

(iv)    the angle turned through by the rotor in coming to rest momentarily before reversing direction.

____________________________________________________________________________________________________________________________

(4)

(Total 8 marks)

(a)     (i)      energy: kinetic energy = ½Iω², → small stored energy
[or less work/energy needed to produce change]
power = rate of energy change, fast change → high power
torque: T = Iα, α large so large torques needed unless I small,
momentum , impulse: L = Iω, impulse = ∆L so unless I small, large
angular impulses are needed
marking: for any one of the above:
for correct consideration (1)
for mathematical justification (1)

4

(ii)     explanations based on I = mr² (1)
low mass, small diameter (1)

(b)     (i)      α =  = 4.8 × 10³ rad s^–2 (1)

(ii)     T = Iα = 4.4 × 10^–5 × 4.8 ×10³ = 0.21(1) N m (1)

(allow C.E. from incorrect value of α from (i))

(iii)     impulse = torque × time = 0.21 × 50 × 10^–3 = 1.1 × 10^–2 N m s (1)
(1.05 × 10^–2 N m s)
(allow C.E. for value of T from (ii))
[or ∆L = I(ω₂ – ω₁) = 4.4 × 10^–5 × 240 = 1.1 × 10^–2 N m s]

(iv)    θ = 25 × 10^–3 = 1.5 rad (1)

4