PHY_10_16_V2_DM_Moment of inertia of a perfectly rigid body

Problems with solution - The moment of inertia of rigid object

1. What is the moment of inertia of a 2-kg long uniform rod with length of 2 m. The axis of rotation located at the center of the rod.

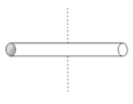
2. What is the moment of inertia of a 2-kg long uniform rod with a length of 2 m? The axis of rotation located at one end of the rod.

3. A 10-kg solid cylinder with a radius of 0.1 m. The axis of rotational located at the center of the solid cylinder, shown in the figure below. What is the moment of inertia of the cylinder?

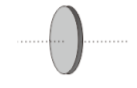
4. A 20-kg uniform sphere with the length of 0.1 m. The axis of rotation located at the center of the sphere shown in the figure below.

5. A 2-kg rectangular thin plate with a length of 0.5 m and width of 0.2 m. The axis of rotation located at the center of the rectangular plat shown in the figure below. What is the moment of inertia of the rectangular?

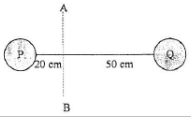
6. Two balls connected by a rod, as shown in the figure below. Ignore rod’s mass. Mass of ball P is 600 gram and mass of ball Q is 400 gram. What is the moment of inertia of the system about AB?

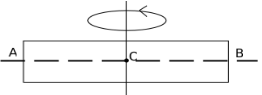
7. The Rod of AB with mass of 2-kg rotated about point A, the moment of inertia of the rod is 8 kg m². If rotated about point O (AO = OB),what is the moment of inertia of the rod.

8. Two balls connected by a rod as shown in figure below. Ignore rod’s mass. What is the moment of inertia of the system.

Solution of problems

1. Known :

Mass of rod (M) = 2 kg

The length of rod (L) = 2 m

Wanted: Moment of inertia

Solution :

The formula of the moment of inertia when the axis of rotation located at the center of long uniform rod :

I = (1/12) M L2

I = (1/12) (2 kg)(2 m)²

I = (1/12) (2 kg)(4 m²)

I = (1/12)(8 kg m²)

I = 8/12 kg m²

I = 2/3 kg m²

2. Known :

Mass of rod (M) = 2 kg

The length of rigid rod (L) = 2 m

Wanted: Moment of inertia

Solution :

The formula of the moment of inertia when the axis of rotation located at one end of the rod :

I = (1/3) M L²

I = (1/3) (2 kg)(2 m)²

I = (1/3) (2 kg)(4 m²)

I = (1/3)(8 kg m²)

I = 8/3 kg m²

3. Known :

Mass of solid cylinder (M) = 10 kg

Radius of cylinder (L) = 0.1 m

Wanted: The moment of inertia

Wanted: The moment of inertia

Solution :

The formula of moment inertia when the axis of rotation located at the center of cylinder :

I = (1/2) M R²

I = (1/2) (10 kg)(0.1 m)²

I = (1/2) (10 kg)(0.01 m²)

I = (1/2)(0.1 kg m²)

I = 0.05 kg m²

4. Known :

Mass of sphere (M) = 20 kg

The radius of sphere (L) = 0.1 m

Wanted: a moment of inertia

Solution :

The formula of the moment of inertia when the axis of rotation located at the center of the sphere :I = (2/5) M R²

I = (2/5)(20 kg)(0.1 m)²

I = (2/5)(20 kg)(0.01 m²)

I = (2/5)(0.2 kg m²)

I = 0.4/5 kg m²

I = 0.08 kg m²

5.Known :

Mass of rectangular plat (M) = 2 kg

The length of plat (a) = 0.5 m

The width of plat (b) = 0.2 m

Wanted : Moment of inertia

Solution :

Formula of moment of inertia when the axis of rotation located at the center of plat :

I = (1/12) M (a² + b²)

I = (1/12)(2)(0.52 + 0.22)

I = (2/12)(0.25 + 0.04)

I = (1/6)(0.29)

I = 0.29/6 kg m²

6. Known :

The axis of rotation is AB.

m_p = 600 gram = 0.6 kg, m_q = 400 gram = 0.4 kg

r_p = 20 cm = 0.2 m, r_q = 50 cm = 0.5 m

Wanted : The moment of inertia of the system

Solution :

I = m_p r_p² + m_q r_q²

I = (0.6 kg)(0.2 m)² + (0.4 kg)(0.5 m)²

I = (0.6 kg)(0.04 m²) + (0.4 kg)(0.25 m²)

I = 0.024 kg m² + 0.1 kg m²

I = 0.124 kg m²

7. Mass of rod AB (m) = 2 kg

If rotated about point A so that the radius of rotation (r) = length of AB = r then the moment of inertia (I) = 8 kg m²

Wanted: If rotated about point O so that the radius of rotation (r) = length of AO = length of OB = 1/2 r then what is the moment of inertia of the rod.

Solution :

I = m r²

8 kg m² = (2 kg) r²

8 m² = (2) r²

r² = 8 m² / 2

r² = 4 m²

r = 2 meters

If rotated about point O so ½ r = 1 meter, then the moment of inertia :

I = m r² = (2 kg)(1 m)² = (2 kg)(1 m²) = 2 kg m²

8. Mass of ball A (m_A) = 200 gram = 0.2 kg

Mass of ball B (m_B) = 400 gram = 0.4 kg

Distance between ball A and the axis of rotation (r_A) = 0

Distance between ball B and the axis of rotation (r_B) = 25 cm = 0.25 m

Wanted : Moment of inertia of the system

Solution :

The moment of inertia of ball A :

I_A = (m_A)(r_A²) = (0.2)(0)² = 0

The moment of inertia of ball B :

I_B = (m_B)(r_B²) = (0.4)(0.25)² = (0.4)(0.0625) = 0.025 kg m²

The moment of inertia of system :

I = I_A + I_B = 0 + 0.025 = 0.025 kg m² = 25 x 10^-3 kg m²

Скачано с www.znanio.ru