План 6

Тема урока: « Противоположные числа. Модуль числа»

Цель урока: ввести понятие противоположных чисел, их расположения в ряде целых чисел и на координатной оси.

Задачи урока: формировать умения находить число, противоположное данному.

Планируемые результаты:

Предметные: знать определение противоположных и целых чисел, определение модуля числа; уметь находить координаты точек на прямой,  применять положительные и отрицательные числа для выражения , изменения величины.

Метапредметные: Коммуникативные: формировать навыки учебного сотрудничества в ходе индивидуальной и групповой работы.

Регулятивные: определять последовательность промежуточных целей с учетом конечного результата, составлять план последовательности действий.

Познавательные: сопоставлять характеристики объектов по одному или нескольким признакам, выявлять сходства и различия объектов.

Личностные: Формирование устойчивой мотивации к индивидуальной деятельности по самостоятельно составленному плану.

Техническое обеспечение урока: компьютер

Дополнительное методическое и дидактическое обеспечение урока (возможны ссылки на интернет-ресурсы): рабочая тетрадь 6 класс М.К. Потапов, А.В. Шевкин.

Содержание урока:

I.                   Организационный момент.

II.                Проверка домашнего задания.

Заслушивание сообщения на тему « Где вы встречались с отрицательными и положительными числами?»

III.             Актуализация опорных знаний.

1. устный опрос:

- какие числа называются положительными? Отрицательными?

-какое число не положительно и не отрицательное?

Что такое координатная прямая?

Какую координату имеет начало координат?

Даны числа: -9, 12, -25, 0, , - 1, 15, -360, 26.

- назовите отрицательные, положительные, натуральные и дробные числа.

IV. Изучение темы урока.

На прошлом уроке мы познакомились с координатной прямой, познакомились с положительными и отрицательным числами.

Координата точки показывает, на каком расстоянии от начала отсчёта расположена точка. Так точка с координатой 4 расположена правее нуля на расстоянии четырёх единичных отрезков. А точка с координатой -4 расположена левее нуля на расстоянии четырёх единичных отрезков.

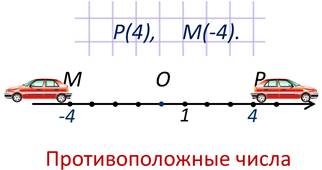
Обратите внимание, чтобы попасть из начала отсчёта в эти точки, надо преодолеть одинаковые расстояния, но в ПРОТИВОПОЛОЖНЫХ направлениях.

Числа 4 и -4 называются противоположными числами.

4 противоположно -4, а -4 противоположно 4.

Числа -5 и 5 тоже будут противоположными.

Определение

Два числа, отличающиеся друг от друга только знаками, называют противоположными числами.

Для числа а число -а называют противоположным.

Число -5 противоположно 5.

Запись «-(-5)» означает число, противоположное числу -5. А так как числу -5 противоположно число 5, то

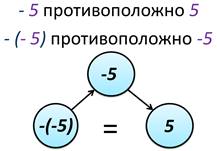
Выражение -(-5) можно читать «минус минус 5» или «число, противоположное числу -5».

Для каждого числа есть противоположное ему число.

Но как же быть с числом 0? Оказывается, число 0 противоположно самому себе.

Натуральные числа, противоположные им числа и нуль называют целыми числами.

V.Закрепление новой темы.

1. Работа по учебнику.

1) Выполнить устно № 208-210

2) Выполнить письменно № 214, 215

      2. Дополнительные задания.

  1)  Сколько целых чисел расположено правее числа – 7, но левее числа 17?

Решение: от – 7 до 0 таких чисел 6 ( -6, -5, -4, -3, -2, -1), само число 0, и от 0 до 17 целых чисел 16 ( 1, 2, 3, …, 15, 16). Итак: 6 + 1 + 16 = 23.

2) Сколько целых чисел расположено правее числа – 17, но левее числа – 9?

Решение: Между числами – 17 и – 9 расположены числа -16, -15, -14, -13, -12, -11, -11, - 10. Всего таких чисел 7.

3)  Кузнечик может прыгнуть с любого числа на соседнее. Какое наименьшее количество прыжков ему надо совершить, чтобы с числа – 3 попасть на число 23?

Решение: от – 3 до 0 получаем 3 прыжка, от 0 до 23 получаем 23 прыжка, всего 3 + 23 = 26 прыжков.  

4) Вычислите с помощью ряда целых чисел6 5-19.

Решение: мы должны от целого числа 5 переместиться влево на 19 шагов или чисел, от 5 до 0 имеем пять шагов, остается проделать 14 шагов, значит ответ – 14.

VI. итоги урока. Рефлексия.

- Какой вывод из изученного можно сделать?

- Число, противоположное отрицательному – положительное, а число, противоположное положительному – отрицательное.

VII. Домашнее задание: Прочитать п. 2.2 Письменно « 226