План-конспект урока геометрии в 7 классе по теме: "Внешний угол треугольника"

Геометрия 7 класс   Урок 41.                                                                      Дата:                                                                      

 Тема. Внешний угол треугольника. Теорема о внешнем угле треугольника

  Цель: сформировать понятие и вывести свойство внешнего угла треугольника в процессе отбора нужной информации путем применения ранее полученных знаний.

 Планируемые результаты.

Предметные: создать  условия для усвоения понятия внешнего угла треугольника и применения его свойства при решении задач.

Метапредметные: развивать умение выбирать из потока информации необходимую для решения математических задач; продолжать работу по формированию у каждого учащегося личной потребности в последовательной деятельности, развитию творческих способностей учащихся; развивать устную и письменную речь.                                                                                                 Личностные: продолжить работу по формированию ответственности учащихся за свою деятельность на уроке, умений самостоятельно добывать знания, воспитывать у учащихся чувство удовлетворения от возможности показать на уроке свои знания не только по математике, но и в других областях школьных знаний; проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений

 Предметные умения  (УУД)

Познавательные: владеют геометрическим языком, умеют использовать его для описания предметов окружающего мира, приобретают навыки геометрических построений; умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки

Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей; осуществляют самоанализ и самоконтроль

Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками

 Тип урока: изучение нового материала

Техническое обеспечение: компьютер, проектор, интерактивная доска

Оборудование: линейка, карандаш, треугольник; презентация.

Литература. Учебник Геометрия 7-9 классы: учеб. для общеобразоват. учреждений                      Л.С. Атанасян, В.Ф. Бутузов.

  Этапы урока:

I. Организационный момент.  1 мин                                                                                                                     II. Актуализация знаний.  Вычислить все неизвестные углы треугольника  7 мин                                              III. Изучение нового материала. 14 мин                                                                                                                IV. Физкультминутка 1 мин                                                                                                                                         V. Закрепление знаний.                                                                                                                               1. Решение задач в тетрадях 5 мин                                                                                                        2. Самостоятельная работа 12 мин.

VI. Домашнее задание 1 мин                                                                                                                                              VII. Итог урока   3 мин                                                                                                                                                VIII. Рефлексия 1 мин

Ход урока

I. Организационный момент                                                                                                                             - приветствие; определение отсутствующих; проверка готовности учащихся к уроку.

ІI. Актуализация знаний

1. Один из учащихся доказывает теорему о сумме углов треугольника.
2. Второй учащийся решает на доске задачу № 230.
3. Устно со всем классом решаем задачи по готовым чертежам.

Вычислить все неизвестные углы треугольника

1. Найдите неизвестный угол треугольника, если у него два угла равны 50° и 60°. (Слайд 2, рисунок 1). 
2. Найдите неизвестный угол треугольника, если у него один угол прямой, а другой равен 20°. (Слайд 2, рисунок 2)
3. Найдите угол при основании равнобедренного треугольника, если угол между боковыми сторонами 40°. (Слайд 2, рисунок 3)
4. Найдите угол между боковыми сторонами равнобедренного треугольника, если угол при основании у него равен 30°. (Слайд 2, рисунок 4)
5. Вычислить все неизвестные углы прямоугольного равнобедренного треугольника. (Слайд 3, рисунок 1)
6. Вычислить все неизвестные углы равностороннего треугольника. (Слайд 3, рисунок 2)
7. Вычислите все неизвестные углы треугольников (Слайд 4)
8. Определите вид треугольника (Слайды 5, 6, 7)

III. Изучение нового материала.

Вступительное слово учителя (постановка проблемы урока).

Ребята, сегодня перед нами стоит такая проблема: нам нужно познакомиться ещё с одним углом, с которым мы раньше не встречались, у которого так же есть своё свойство. Мы сегодня повторили многие углы, которые мы знаем, и некоторые из них помогут нам в решении нашей поставленной задачи.

1. Ввести понятие внешнего угла треугольника:

Ребята, давайте выполним следующую практическую работу, а именно:

• Постройте произвольный треугольник АВС
• Проведите луч ВД так, чтобы полученный угол был смежным с углом В треугольника АВС.

• Назовите получившийся угол (может быть два варианта АВД или СВД)
• Где они лежат по отношению к треугольнику, внутри или вне его?
• Эти углы имеют специальное название – они называются внешними углами треугольника.
• А теперь запишем тему урока “Внешний угол треугольника и его свойство”
• А как вы думаете, можно ли при других вершинах этого треугольника построить внешние углы?
• Итак, попробуем сформулировать определение внешнего угла треугольника.

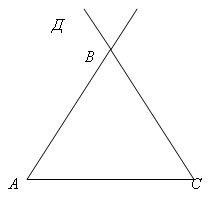
Вывод: Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника.

  Физкультминутка. Упражнения для глаз.

• Что мы знаем об углах треугольника? (°)
• Что мы знаем о смежных углах? (Сумма смежных углов равна 180° или °)
• Посмотрите на эти равенство повнимательнее и скажите , что из них следует? ()
• Какой можно сделать вывод?

Вывод: Внешний угол треугольника равен сумме двух других углов треугольника, не смежных с ним.

Это и есть свойство внешнего угла треугольника, и мы его вместе доказали.

IV. Закрепление знаний

1. Решение задач

1. Устно решить задачу: в треугольнике АВС =110°.

Чему равны:

а) сумма остальных внутренних углов треугольника?

б) внешний угол при вершине С?

2. По готовому чертежу на доске устно решить задачу:

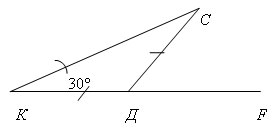
Найдите внутренние и внешний угол СДF треугольника КСД.

3. Решить задачу № 232 под руководством учителя на доске и в тетрадях.

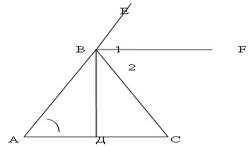
Дано: внешний угол треугольника АВС; .

Доказать: равнобедренный.

Решение

Проведем биссектрисы ВF и ВД смежных углов СВЕ и АВС, тогда ВF || АС, так как , а углы 1 и А соответственные при пересечении прямых ВF и АС секущей АВ, ВД , так как ВД , а BF || AC.

В треугольнике АВС биссектриса ВД является высотой, следовательно, треугольник АВС – равнобедренный (см. задачу № 133)

2. Обратное утверждение также верно, а именно: если треугольник равнобедренный, то внешний угол при вершине, противолежащей основанию треугольника, в два раза больше угла при основанию Действительно, этот внешний угол равен сумме двух углов при основании равнобедренного треугольника, с так как углы при основании равны, то данный внешний угол в два раза больше угла при основании треугольника.

2. Самостоятельная работа обучающего характера (на два варианта)

Вариант 1

1. Один из углов равнобедренного треугольника равен 96°. Найдите два других угла.

2. В треугольнике СДЕ с углом  проведена биссектриса СF, Найдите 

Вариант 2

1. Один из углов равнобедренного треугольника равен 108°. Найдите два других угла.

2. В треугольнике СДЕ проведена биссектриса СF, , .

Найдите 

V. Домашнее задание: изучить пункт  31, стр.70; решить задачи № 233, 235.

  VI. Итоги урока.

- Что такое внешний угол треугольника?

- Какое свойство внешнего угла мы сегодня доказали?

- Чему вы сегодня научились?

- Какие теоремы сегодня на уроке мы использовали при решении задач?

Самооценка детьми собственной деятельности.

VII.   Рефлексия

Определите истинность для себя одного из следующих утверждений:

«Я понял, что такое внешний угол треугольника»,

«Я знаю, как находить градусную меру внешнего угла треугольника»,

«У меня остались нерешенные вопросы».

Отобразите свои ответы в виде смайликов на листочке.  

Скачано с www.znanio.ru