План конспект урока на тему: Комбинаторика

Тема: Основные понятия комбинаторики

Цели:

- обучения:

создавать условия для осознанного понимания решения простейших задач на применение элементов комбинаторики; изучить формулы размещения, перестановки и сочетания; сформировать у студентов первичные умения и навыки решения задач.

- развития:

развивать познавательный интерес студентов, логическое мышление, умение применять знания в изменённой ситуации, делать выводы и обобщения; развивать умения сравнивать, систематизировать, обобщать; навыки контроля и самоконтроля.

- воспитания: 

формировать научное мировоззрение у студентов, культуру математической речи, информационную и коммуникативную культуру студентов; воспитание дружелюбного отношения друг другу, умение работать в коллективе.

Тип учебного занятия: комбинированный урок

Ход занятия

1. Орг. момент:Преподаватель проверяет готовность к уроку.

Я рада приветствовать всех Вас на сегодняшнем уроке.

2. Актуализация знаний, умений и навыков

Прежде чем перейти к изучению нового материала, проведем небольшую разминку по ранее изученному материалу.

Что называется первообразная?

Дайте определение интеграла

Теперь давай те вспомним формулы интегрирования, я буду показывать  интеграл, а его ответ на доске. вы выбираете и переворачиваете лист, перевернув все листы вы узнаете навание новой темы

Комбинаторика - раздел математики, в котором решаются задачи на составление различных комбинаций? Сейчас я предлагаю Вам решить задачу.

Туристическая фирма планирует посещение туристами в Италии трех городов: Венеции, Рима и Флоренции. Сколько существует вариантов такого маршрута?

ВРФ ВФР РФВ РВФ ФРВ ФВР (6)

Задачи такого типа называются комбинаторными задачами.

3. Изучение и усвоение новых знаний

Вы сейчас предложили несколько способов решения выше указанной задачи. Но есть более простой способ решения данной задачи – это решение с использованием основных понятий комбинаторики (перестановки, размещения, сочетания). Давайте более подробно остановимся на каждом понятии.

1. Перестановки. Перестановками из n элементов называются такие соединения из всех nэлементов, которые отличаются друг от друга порядком расположения элементов.

Число перестановок из n элементов обозначается символом P_n и вычисляется по формуле:

P_n = n!

Вернемся к нашей задаче. Нам известно, что туристическая фирма планирует посещение туристами в Италии трех городов: Венеции, Рима и Флоренции. Сколько существует вариантов такого маршрута?

P_n = n! = 3! = 1*2*3=6 (способов)

Ответ: 6 способов.

Рассмотрим еще одну задачу.

В ящике находится 15 деталей. Сколькими способами можно взять 4 детали?

2. Сочетания. Сочетаниями из n элементов по k в каждом называются такие соединения, которые отличаются друг от друга хотя бы одним элементом. Количество сочетаний обозначается   и вычисляется по формуле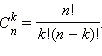

Вернемся к задаче.

3. Размещения. Размещениями из n элементов по k в каждом называются такие соединения, которые отличаются друг от друга либо самими элементами (хотя бы одним), либо порядком их расположения. Количество размещений обозначается  и вычисляется по формуле

Предлагаю Вам составить задачу на нахождения количества размещений.

Пример. Сколько различных двузначных чисел можно составить из множества цифр , причем так, чтобы цифры числа были различны? 

4. Первичный контроль знаний

1) Решение простейших комбинаторных задач

Студенты работают у доски, решают простейшие комбинаторные задачи.

Сколькими способами можно рассадить 5 человек за столом? 

В студенческой группе 23 человека. Сколькими способами можно выбрать старосту и его заместителя?  способами. 

Сколькими способами из колоды в 36 карт можно выбрать 3 карты?

2) Найти ошибки в решениях задач:

Проверьте, верно, ли решены задачи:

Сколькими способами из восьми человек можно избрать комиссию, состоящую из пяти членов?

С = 

Ответ: 56. (верно)

Сколько четырехбуквенных слов можно образовать из букв слова сапфир?

P₄=4! = 1*2*3*4 =24 (неверно)

А.

3) Студенты работают самостоятельно по вариантам. Взаимопроверка.

1 вариант.

Сколько различных четырехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6?

Решение. Общее число комбинаций равно числу размещений из 6 элементов по 4  

2 вариант

В группе 10 студентов. Сколькими способами можно выбрать из этой группы троих студентов для участия в конференции?

Решение. Число способов равно числу сочетаний из 10 элементов по 3 элемента: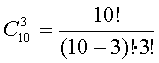 

=120

Самостоятельная работа, работа в парах, публичное выступление

раздаточный материал (карточка с задачами)

Домашнее задание

Задача на «3»

1.      Сколько различных четырехзначных чисел можно составить из цифр 2, 3, 5, 7.

Задачи на «4»

2.      Восемь студентов обменялись рукопожатиями. Сколько было рукопожатий?

3.      Сколькими способами можно составить трехцветный полосатый флаг из пяти различных по цвету отрезков материи?

Задача на «5»

4.      Сколько словарей надо издать, чтобы можно было выполнять переводы с любого из шести языков на любой из них?

Вы молодцы!

Каждый из вас «научился тому, что следует знать».

Спасибо за урок!