План- конспект урока "Тригонометрическая форма комплексного числа"

Министерство образования Чувашской Республики

Государственное автономное профессиональное

образовательное учреждение Чувашской Республики

 «Чебоксарский техникум транспортных и строительных технологий»

План конспект занятия по дисциплине ЕН.01Математика

На тему: «Тригонометрическая форма комплексного числа»

Разработала:

преподаватель математики

Андреева Н.А.

Чебоксары

2025

Содержание

Пояснительная записка                                                                            4

Дидактическая структура урока                                                              5

Учебно-методическая карта урока                                                          6

Ход урока                                                                                                8

Список используемой литературы                                                          15

Пояснительная записка

Методическая разработка учебного занятия по дисциплине ЕН.01Математика на тему «Тригонометрическая форма комплексного числа» с применением основных методов обучения: фронтальный, проблемный, частично-поисковый, наглядно-иллюстративный, информационно-коммуникационный.

Цель изучения данной темы: познакомить студентов с новой формой комплексного числа, развитие логического мышления и воображения, воспитывать активность, самостоятельность, интерес к предмету.

Описание материала: данная методическая разработка предназначена для изучения темы «Тригонометрическая форма комплексного числа» студентами 2 курса учреждений среднего профессионального образования, материал будет полезен преподавателям математики в старших классах и средних специальных учебных заведений. Занятие построено с применением методов проблемного, частично-поискового и дифференцированного обучения.

Дидактическая структура урока

Цели урока:

Образовательные:

·        включить новую информацию в структуру прежних знаний;

·        расширить сведения учащихся о числах;

·        научить записать комплексные числа, заданные в алгебраической форме, в тригонометрической форме и обратно.

Развивающие:

·        развивать пространственное мышление, пространственную абстракцию;

·        развивать логическое мышление;

·        развивать эмоционально-положительное отношение к изучению математики.

Воспитательные:

·        воспитывать активность, самостоятельность, интерес к предмету;

·        показать красоту и необычайность математики.

Тип урока:

·        Урок открытия и первичного закрепления новых знаний.

Формы организации познавательной деятельности:

·        Исследование, фронтальная работа, индивидуальная работа, дифференциация.

Средства обучения:

·        компьютер;

·        презентация Power Point;

·        проектор с мультимедийным экраном;

Перечень рассматриваемых вопросов:

·        геометрическая интерпретация комплексного числа;

·        понятие модуля комплексного числа;

·        понятие аргумента комплексного числа;

·        понятие тригонометрической формы комплексного числа;

·        перевод комплексного числа в тригонометрическую форму.

Учебно-методическая карта урока

Ход урока

1.Организационный момент

Здравствуйте, ребята. Садитесь.

Наш урок я хочу начать со слов чешского педагога Яна Амоса Каменского «Считай несчастным тот день или тот час, в который ты не усвоил ничего нового и ничего не прибавил к своему образованию». Задумайтесь над этими словами. Удачи, творчества и новых открытий я вам желаю сегодня на уроке.

Сегодня на уроке продолжим изучение комплексных чисел, вспомним материал прошлого занятия, повторим, рассмотрим еще одну форму записи комплексных чисел, закрепим знания путем решения задач, подведем итоги.  Поэтому будьте собраны, внимательны и наблюдательны.

2.Актуализация знаний

Для начала вспомним что мы знаем о комплексных числах. Давайте вместе ответим на следующие вопросы:

1.     Что такое мнимая единица?

2.     Какие числа называются комплексными? Как они записываются? Как это форма называется? Из каких частей состоит это число?

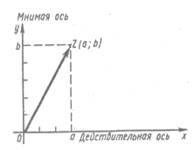
3.     Как геометрически можно изобразить комплексное число, заданное в алгебраической форме?

Комплексное число z=a+bi можно изобразить точкой Z плоскости с координатами (а; b).

4.     Что такое модуль комплексного числа?

5.     По какой формуле вычисляется модуль?

6.     Что такое аргумент комплексного числа?

7.     С помощью каких формул можно вычислить аргумент?

Итак, мы вспомнили основные определения и формулы комплексного числа, записанного в алгебраической форме. А сейчас переходим к новой теме.

3. Изучение нового материала

На прошлом уроке мы говорили, что комплексное число имеет 3 формы, одну мы уже изучили- алгебраическую. Но в электротехнике, электрооборудовании, электронике, автоматике и в других дисциплинах комплексное число записывается в тригонометрической форме. Запишем в тетрадь дату и тему урока «Тригонометрическая форма комплексного числа».

Пусть дается комплексное число в алгебраической форме z=a+bi (1) Наша задача представить это число в тригонометрической форме. Для этого изобразим это число геометрически

и из формул  ;   находим    и . Если в формулу (1) в место   подставим полученные значения, то получим z=a+bi=  z=. Таким образом, любое комплексное число a+bi ≠ 0 можно записать по формуле (2). Где Верно и обратное утверждение: если комплексное число a+bi представлено в виде (2), где ,  a+bi)

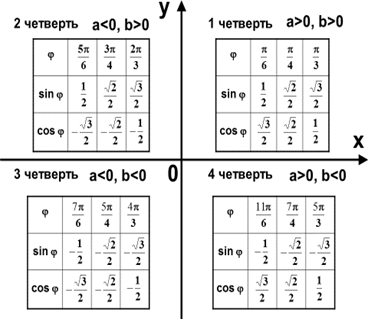
Формула (2) называется тригонометрическая форма комплексного числа. Итак, алгоритм перехода от алгебраической формы комплексного числа к тригонометрической:

1)   Находим модуль комплексного числа по формуле

2)  Для нахождения  определяем геометрически, в какой четверти находится радиус- вектор  

3)   Составляем уравнения ;   и по решению одного из них находим угол

4)Записываем комплексное число число z в тригонометрической форме.

Пример: Записать в тригонометрической форме комплексное число z=1+i

Решение: 1) Так как a =1, b =1, то

2) Изобразим число к.ч. z геометрически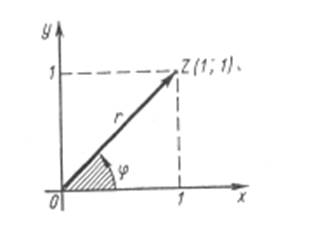

Мы видим, что числу z соответствует точка Z, лежащая в 1 четверти, и вектор

3)Составим отношения  ;  , т.е. ,  Этим соотношениям соответствует в 1 четверти угол

4)Тригонометрическая форма к. ч. имеет вид

z=1+i=() или z=1+i=()

4. Закрепления изученного материала

Пример 1: Записать в тригонометрической форме комплексное число

z= -2+2i

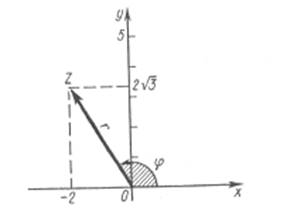
Пример2: Записать в тригонометрической форме комплексное число z=- 3i

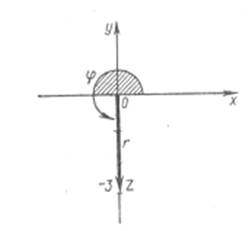
Пример3: Записать в тригонометрической форме комплексное число z= 5

5.Обобщение и систематизация изученного материала

А.Н.Крылов говорил: «Теория без практики мертва, практика без теории невозможна. Для теории нужны знания, для практики сверх того, и умения».

Вот теперь, вы должны проявить свои умения выполнив задания самостоятельной работы в течение 10 минут.

Вариант 1

Пример 1: Записать в тригонометрической форме комплексное число z=3+3i

Пример 2: Записать число в алгебраической форме z=4 ()

Вариант 2

Пример 1: Записать в тригонометрической форме комплексное число z=2+2i

Пример 2: Записать число в алгебраической форме z=3 ()

5. Домашнее задание

Записать в тригонометрической форме комплексное число z=2-2i

6.Рефлексия

·     Мне больше всего удалось…

·     Для меня было открытием то, что …

·     Что на ваш взгляд не удалось? Почему?

Какое у тебя было настроение на паре:

9. Итог урока

 Спасибо за урок. Все активно работали. Молодцы!

Список используемой литературы

1.     Математика: учебник для учреждений нач. и сред. проф. образования /М.И. Башмаков – М. «Академия», 2013

2.     Математика. Задачник: учеб. Пособие для образоват. учреждений нач. и сред. проф. образования /М.И. Башмаков – М. «Академия», 2013

3.     Математика: Учебное пособие для средних специальных учебных заведений / Е.В.Филимонова – Ростов н/Д: Феникс, 2004

4.     Лисичкин В. Т. Математика в задачах с решениями: учеб. пособие / В. Т. Лисичкин, И. Л. Соловейчик. - 3-е изд., стер. - СПб. [и др.]: Лань, 2011 (Архангельск). - 464 с