Поделиться
ПЛОЩАДЬ МНОГОУГОЛЬНИКА2.docx
ПЛОЩАДЬ МНОГОУГОЛЬНИКА
Цели: вывести формулу площади прямоугольника, научить находить площадь прямоугольника.
Ход урока
I. Проверка домашнего задания.
1. Ответить на вопросы учащихся.
2. Выполнить задания (устно):
1) Площадь параллелограмма АВСD равна S. Найдите площади треугольников АВС и АВD.
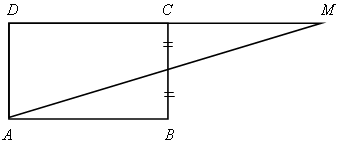
2) Площадь прямоугольника АВСD равна Q. найдите площадь треугольника АМD.
|
|
3) АВСD – прямоугольник, точки Е и F – середины его сторон АD и ВС. Заштрихованный квадрат представляет собой единицу измерения площадей. Найдите площадь трапеции KМNP. |
II. Изучение нового материала.
Выполнить задание:
1. Докажите, что два прямоугольника равны, если равны их смежные стороны.
|
|
2. АВСD – квадрат, MN || АВ, ЕF || ВС. Найдите площадь четырехугольника АFКМ, если АМ = СЕ = 3 см. DЕ = 6 см. 3. Доказать теорему о площади прямоугольника. (Заготовить чертеж заранее из учебного пособия, рис. 181.) |
III. Закрепление изученного материала.
№ 452 (а, в), № 453 (а, б).
|
|
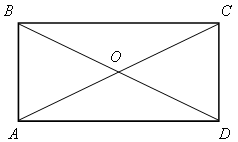
1) РАВСD = 40, АD = 3СD. Найти: SАВСD. 2) АD = 20, SDOC = 60. Найти: СD. Решение Проведем через точку О прямые, параллельные
сторонам прямоугольника, и получим 8 равных прямоугольных треугольников, с
площадью |
SАВСD = 8 · 30 = 240;
DС = 
= 12.
IV. Итоги урока.
Домашнее задание: вопрос 3, с. 133; №№ 452 (б, г), 453 (в), 448.
1.
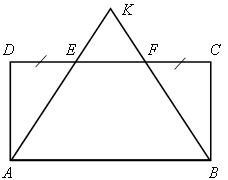
Периметр прямоугольника равен 44 см, а DС : АD = 7 : 4. Найдите
площадь треугольника АВK, если DЕ = FC = 
ЕF.
2. SАСD = 28, АВ = АD + 1. Найти РАВСD.
3. Вырезать из бумаги два равных прямоугольных треугольника и составить из них:
1) равнобедренный треугольник;
2) прямоугольник;
3) параллелограмм, не являющийся прямоугольником.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
