Поделиться
ПЛОЩАДИ ПАРАЛЛЕЛОГРАММА,2.docx
ПЛОЩАДИ ПАРАЛЛЕЛОГРАММА,
ТРЕУГОЛЬНИКА И ТРАПЕЦИИ
Цели: доказать теорему об отношении площадей треугольников, имеющих по равному углу; познакомить учащихся с решением задач по этой теме.
Ход урока
I. Проверка домашнего задания.
Выполнить устно:
|
1) SDАВС – ? |
2) SDАВС – ? |
|
|
|
|
|
|
3)
|
СМ
– медиана Найти отношение площадей
|
|
Ответ: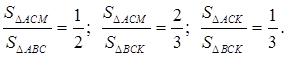 
|
4)
|
Докажите,
что SMBKD = Решение
SАВСD = SDАDВ + SDDВС SМDKВ = SDМDВ + SDDКВ |
.
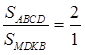II. Объяснение нового материала.
Доказательство теоремы об отношении площадей треугольников, имеющих по равному углу, рекомендуется провести самому учителю.
III. Закрепление изученного материала.
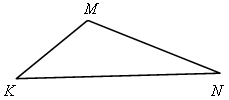
1. Дано:
А
= K,
АС = 5 см, АВ = 3 см, KN = 7 см, KМ = 2 см.
Найти: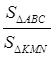 
.
Решение
|
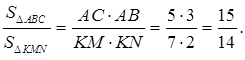
2. |
Дано: АО = 8 см; ОВ = 6 см; ОС = 5 см; ОD = 2 см; SDАОВ = 20 см2. Найти: SDСОD. |
Решение
. 
. 
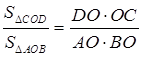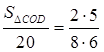3. Площадь одного равностороннего треугольника в три раза больше, чем площадь другого равностороннего треугольника. Найдите сторону второго треугольника, если сторона первого равна 1.
Решение
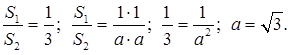
№ 479 (б).
Решение
|
|
|
IV. Самостоятельная работа обучающего характера.
Вариант I
|
|
АО = ОВ, ОС = 2 · ОD SDАОС = 12 см2. Найти: SDВОD. |
Вариант II
|
|
ОВ = ОС; ОD = 3ОА SDАОС = 16 см2. Найти: SDВОD. |
Вариант III
|
|
АО = АВ; АС || ВD. Докажите, что SDОВС = SDОАD. |
V. Итоги урока.
Домашнее задание: § 2, вопрос 6, с. 134; №№ 469, 472, 479 (а).
Для желающих.
1. В четырехугольнике диагонали равны 8 см и 12 см и пересекаются под углом 30° друг к другу. Найдите площадь этого четырехугольника.
Решение
|
|
SАВСD = SDАВС + SDАDС =
|
SАВСD = 
= 24 (см2).
2. В треугольнике точка пересечения биссектрис удалена от прямой, содержащей одну из сторон на 1,5 см. Периметр треугольника равен 16 см. Найдите его площадь.
Решение
|
|
1. Расстояние от точки пересечения биссектрис до прямых, содержащих стороны треугольника, равны как радиусы вписанной окружности. SDАВС = SDАВО + SDВОС + SDАОС =
|
= 
r (AB + BC + AC)
= ∙
1,5 ∙ 16 = 12 (см2).
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
АСВ.
