Подготовка к ЕГ по математике. Задачи с параметрами для 5-9 классов

5 класс

275. Какое число надо подставить вместо a, чтобы корнем уравнения:

1) (x + a) – 7 = 42  было число 22;

2) (a – x) + 4 = 15  было число 3?

276. Какое число надо подставить вместо a, чтобы корнем уравнения:

1) (x – 7) + a = 23  было число 9;

2) (11 + x) + 101 = a  было число 5?

 

6 класс

1199. При каком значении a уравнение:

1)  имеет корень, равный числу 4;

2)  имеет корень, равный числу ?

1200. При каком значении a уравнение:

1)  имеет корень, равный числу  –3;

2)  имеет корень, равный числу 1?

1203.* При каких значениях a не имеет корней уравнение:

1) ;

2)  ?

1204.* Найдите все целые значения a, при которых корень уравнения является целым числом:

1) ;

2) .

1205.* Найдите все целые значения m, при которых корень уравнения является натуральным числом:

1) ;

2) .

 

7 класс

Линейное уравнение с одной переменной

Уравнение ax = b	a ¹ 0	a = 0, b = 0	a = 0, b ¹ 0
		x — любое число	корней нет

Пример 2. Решите уравнение:

1) (a – 1)x = 2;                     2) (a + 9) x = a + 9.

Решение. 1) При a = 1 уравнение принимает вид 0x = 2. В этом случае корней нет. При a ¹ 1 получаем: .

Ответ: если a = 1, то уравнение не имеет корней; если a ¹ 1, то .

2) При a = – 9 уравнение принимает вид 0x = 0. В этом случае корнем уравнения является любое число. При a ¹ – 9 получаем: x = 1.

Ответ: если a = – 9, то x — любое число; если a ¹ – 9, то x = 1.

 

 

53. При каком значении a уравнение:

1)  имеет корень, равный числу 3;

2)  имеет корень, равный числу ?

54. При каком значении a уравнение:

1)  имеет корень, равный числу ;

2)  имеет корень, равный числу 2?

55. Укажите какое-либо значение b, при котором будет целым числом корень уравнения:

1) ;

2) ;

3) ;

4) .

 

 

57. Найдите все целые значения m, при которых является целым числом корень уравнения:

1) mx = 3;

2) (m + 4)x = 49.

58. Найдите все целые значения n, при которых является натуральным числом корень уравнения:

1) nx = –5;

2) (n – 6)x = 25.

59. При каком значении b имеют общий корень уравнения:

1)   и  ;

2) 2y – 9b = 7  и  ?

60. При каком значении c имеют общий корень уравнения:

1)  и ;

2)  и ?

61. При каком значении a не имеет корней уравнение:

1) ;

2) ;

3) ?

62. При каком значении a любое число является корнем уравнения:

1) ;

2) ;

3) ?

63. При каких значениях a имеет единственный корень уравнение:

1) ;

2) ?

64. Решите уравнение:

1) ;                        2) .

65. Решите уравнение .

 

 

70.* При каких целых значениях a корень уравнения:

1) ;

2) ;

3) ;

4)

является целым числом, которое делится нацело на 2?

71.* При каких целых значениях b корень уравнения:

1) ;

2) x – 2 = b;

3) x – 3b = 8

является целым числом, которое делится нацело на 3?

72.* При каких значениях b корень уравнения будет меньше, чем b:

1) ;

2) ?

73.* При каких значениях d корень уравнения будет больше, чем d :

 

1) 4x = d;

2) x = d ?

 

Преобразования многочленов.

Пример 6. При каком значении a уравнение (x + 2)(x + a) – x(x + 1) = 3a + 1 имеет бесконечно много корней?

Решение. Имеем:

x² + ax + 2x + 2a – x² – x = 3a + 1;

ax + x + 2a = 3a + 1;

ax + x = a + 1;

(a + 1)x = a + 1.

Только при a = –1 последнее уравнение принимает вид 0x = 0 и имеет бесконечно много корней.

Ответ: при a = –1.

467. При каком значении a не имеет корней уравнение:

1) (x + 1)(x – 3) – x(x – 3) = ax;

2) x(5x – 1) – (x – a)(5x – 1) = 4x – 2a ;

3) (2x – 5)(x + a) – (2x + 3)(x + 1) = 4?

468. При каком значении a имеет бесконечно много корней уравнение:

1) (x – 4)(x + a) – (x + 2)(x – a) = – 6;

2) x(3x – 2) – (x + 2a)(3x + 2) = 5a + 6 ?

 

Формулы сокращенного умножения.

557. При каком значении b уравнение :

1) имеет бесконечно много корней;

2) не имеет корней;

3) имеет один корень?

558. При каком значении a уравнение :

1) имеет бесконечно много корней;

2) не имеет корней;

3) имеет один корень?

 

Уравнение с двумя переменными.

973. При каком значении a пара чисел (– 4; 2) является решением уравнения:

1) 3x + 5y = a;

2) ax + 5y = 18 ?

974. При каком значении a график уравнения 11x – 13y = a + 4 проходит через начало координат?

975. При каком значении a через точку A(5; –3) проходит график уравнения:

1) 4x – 9y = a;

2) 6x – ay = 15 ?

976. При каком значении a график уравнения ax + 4y = 0 проходит через точку:

1) A(12; – 4);

2) B(0; 2);

3) O(0; 0) ?

977. При каком значении b график уравнения 5x + by = 0 проходит через точку:

1) M(– 4; –10);

2) N(0; 1);

3) K(–2; 0) ?

 

Системы линейных уравнений.

1014. Пара чисел (6; 4) является решением системы уравнений:

1)

2)

Найдите значения a и b.

1015. При каких значениях a и b пара чисел (–2; 3) является решением системы уравнений

1020. При каких значениях a не имеет решений система уравнений

1021. При каком значении a имеет бесконечно много решений система уравнений:

1)

2)

1022. При каких значениях a система уравнений:

1)  не имеет решений;

2)  имеет бесконечно много решений?

1023. Подберите такие значения a и b, при которых система уравнений

1) имеет бесконечно много решений;

2) имеет единственное решение;

3) не имеет решений.

1024. Подберите такие значения m и n, при которых система уравнений

1) имеет бесконечно много решений;

2) имеет единственное решение;

3) не имеет решений.

8 класс

Пример 6. Решите уравнение (a² – 9) x = a + 3.

Решение. Запишем данное уравнение в виде (a + 3)(a – 3)x = a + 3 и рассмотрим три случая.

1) a = 3.

Тогда получаем уравнение 0x = 6, которое не имеет корней.

2) a = –3.

В этом случае получаем уравнение 0x = 0, корнем которого является любое число.

3) a ¹ 3 и a ¹ –3.

Тогда .

Ответ: если a = 3, то уравнение не имеет корней; если a = –3, то корнем является любое число; если a ¹ 3 и a ¹ –3, то . ●

60. Для каждого значения a решите уравнение:

1) ax = 1;                             3) (a – 6)x = a² – 12a + 36;

2) ax = a;                             4) (a² – 4)x = a – 2.

61. Для каждого значения a решите уравнение:

1) (a + 3)x = 3;                    2) (a² – 9a)x = a² – 18a + 81.

219.* Для каждого значение a решите уравнение:

1) ;                          4) ;

2) ;                          5) ;

3) ;                       6) .

220.* При каких значениях a уравнение  не имеет корней?

221.* При каких значениях a уравнение  имеет один корень?

 

Арифметический квадратный корень

 

416.* Для каждого значения a решите уравнение:

1) ;         3) ;

2) ;       4) .

417.* При каких значениях a уравнение (– 1)(x – a) = 0 имеет только один корень?

 

Неполные квадратные уравнения

 

Значения коэффициентов b и c	Уравнение	Корни
b = c = 0	ax2 = 0	x = 0
b ¹ 0, c = 0	ax2 + bx = 0	x1 = 0,
b = 0,	ax2 + c = 0	корней нет
b = 0,	ax2 + c = 0	,

 

Квадратные уравнения.

649. При каком значении a уравнение (a – 2)x² + (2a – 1)x + a² – 4 = 0 является:

1) линейным;

2) приведенным квадратным;

3) неполным неприведенным квадратным;

4) неполным приведенным квадратным?

650. Определите, при каком значении a один из корней квадратного уравнения равен 0, и найдите второй корень уравнения:

1) x² + ax + a – 4 = 0;          3) ax² + (a + 3)x + a² – 3a = 0.

2) 4x² + (a – 8)x + a² + a = 0;

 

Пример 3. При каком значении b имеет единственный корень уравнение:

1) 2x² – bx + 18 = 0;             2)* (b + 6)x² – (b – 2)x + 1 = 0 ?

Решение. 1) Данное уравнение является квадратным и имеет единственный корень, если его дискриминант равен нулю. Имеем:

D = b² – 4 × 2 × 18 = b² – 144;

b² – 144 = 0;

b = –12 или b = 12.

Ответ: b = –12 или b = 12.

2) При b = –6 получаем линейное уравнение 8x + 1 = 0, имеющее один корень.

При b ¹ –6 данное уравнение является квадратным и имеет единственный корень, если его дискриминант равен нулю:

D = (b – 2)² – 4(b + 6) = b² – 4b + 4 – 4b – 24 = b² – 8b – 20.

Имеем: b² – 8b – 20 = 0, отсюда  b = –2 или b = 10.

Ответ: b = –2 или b = 10, или b = – 6.

 

688. При каком значении b имеет единственный корень уравнение:

1) 2x² + 4x – b = 0;              2) 3x² – bx + 12 = 0?

689. При каком значении b имеет единственный корень уравнение:

1) 6x² – 18x + b = 0;             2) 8x² + bx + 2 = 0?

690. Докажите, что при любом значении p имеет два корня уравнение:

1) 4x² – px – 3 = 0;               2) x² + px + p – 2 = 0.

691. Докажите, что при любом значении m не имеет корней уравнение:

1) x² + mx + m² + 1 = 0;       2) x² – 2mx + 2m² + 9 = 0.

692. Докажите, что при любом значении b уравнение x² + bx – 7 = 0 имеет два корня.

693.* Решите уравнение:

1) x² + (3a + 1)x + 2a² + a = 0;     3) a²x² – 24ax – 25 = 0;

2) x² – (2a + 4)x + 8a = 0;    4) 3(2a – 1)x² – 2(a + 1)x + 1 = 0.

694.* Решите уравнение:

1) x² – (2a – 5)x – 3a² + 5a = 0;    3) ax² – (a + 1)x + 1 = 0.

2) x² + (3a – 4)x – 12a = 0;

695.* При каком значении b имеет единственный корень уравнение:

1) bx² – 6x – 7 = 0;               3) (b – 4)x² + (2b – 8)x + 15 = 0?

2) (b + 5)x² – (b + 6)x + 3 = 0;

696.* При каком значении b имеет единственный корень уравнение:

1) bx² + x + b = 0;                2) (b + 3)x² + (b + 1)x – 2 = 0?

 

Теорема Виета.

739.* Верно ли утверждение:

1) уравнение  7x² + 4x – a² – 1 = 0 имеет корни разных знаков при любом значении a;

2) если уравнение x² + 6x + a² + 4 = 0 имеет корни, то независимо от значения a они оба отрицательны?

740.* Найдите все целые значения b, при которых имеет целые корни уравнение:

1) x² + bx + 6 = 0;                2) x² + bx – 12 = 0.

741.* Найдите все целые значения b, при которых имеет целые корни уравнение:

1) x² + bx + 8 = 0;                2) x² + bx – 18 = 0.

743.* При каком значении a сумма квадратов корней уравнения  x² – 4x + a = 0 равна: 1) 12; 2) 6?

744.* При каком значении a сумма квадратов корней уравнения  x² + (a – 1)x – 2a = 0 равна 9?

 

796.* Для каждого значения a решите уравнение:

1) ;                   3) ;

2) ;                   4) .

797.* При каких значениях a уравнение  имеет один корень?

 

9 класс

Решение линейных неравенств с одной переменной.

140.^· При каких значениях a уравнение:

1) x² + 3x – a = 0  не имеет корней;

2) 2x² – 8x + 5a = 0  имеет хотя бы один действительный корень?

141.^· При каких значениях b уравнение:

1) 3x² – 6x + b = 0 имеет два различных действительных корня;

2) x² – x – 2b = 0 не имеет корней?

155. При каких значениях a уравнение:

1) 4x + a = 2  имеет положительный корень;

2) (a + 6)x = 3 имеет отрицательный корень;

3) (a – 1)x = a² – 1 имеет единственный положительный корень?

156. При каких значениях m уравнение:

1) 2 + 4x = m – 6 имеет неотрицательный корень;

2) mx = m² – 7m имеет единственный отрицательный корень?

157.* Найдите все значения a, при которых имеет два различных действительных корня уравнение:

1) ax² + 2x – 1 = 0;

2) (a + 1)x² – (2a – 3)x + a = 0;

3) (a – 3)x² – 2(a – 5)x + a – 2 = 0.

158.* Найдите все значения a, при которых не имеет корней уравнение (a – 2)x² + (2a + 1)x + a = 0.

159.* Существует ли такое значение a, при котором не имеет решений неравенство (в случае утвердительного ответа укажите это значение):

1) ax > 3x + 4;                     2) (a² – a – 2)x £ a – 2 ?

160.* Существует ли такое значение a, при котором любое число является решением неравенства (в случае утвердительного ответа укажите это значение):

1) ax > –1 – 7x;                    2) (a² – 16)x ³ a + 4 ?

161.* Для каждого значения a решите неравенство:

1) ax > 0;              3) ax ³ a;              5) (a – 2)x > a² – 4;

2) ax < 1;              4) 2(x – a) < ax – 4;  6) (a + 3)x £ a² – 9.

162.* Для каждого значения a решите неравенство:

1) a²x £ 0;             2) a + x < 2 – ax;   3) (a + 4)x > 1.

 

Системы линейных неравенств

204.* При каких значениях a имеет хотя бы одно решение система неравенств:

1)                              2)

205.* При каких значениях a  не имеет решений система неравенств:

1)                              2)

206.* При каких значениях a множеством решений системы неравенств  является промежуток:

1) (–1; +¥);                         2) [1; +¥) ?

207.* Для каждого значения a решите систему неравенств

208.* Для каждого значения a решите систему неравенств

209.* При каких значениях a множество решений системы неравенств  содержит ровно четыре целых решения?

210.* При каких значениях b множество решений системы неравенств  содержит ровно три целых решения?

211.* При каких значениях a наименьшим целым решением системы неравенств  является число 9?

212.* При каких значениях b наибольшим целым решением системы неравенств  является число –6?

213.* При каких значениях a корни уравнения x² – 2ax + a² – 4 = 0 меньше числа 5?

214.* При каких значениях a корни уравнения x² – (4a – 2)x + 3a² – 4a + 1 = 0 принадлежат промежутку [–2; 8]?

215.* При каких значениях a один из корней уравнения 3x² – (2a + 5)x + 2 + a – a² = 0 меньше –2, а другой — больше 3?

 

Исследование квадратичной функции.

276.* Постройте график функции f(x) = x², определенной на промежутке [a; 2], где a < 2. Для каждого значения a найдите наибольшее и наименьшее значения функции.

364.^· При каком значении b промежуток (–¥; 2] является промежутком возрастания функции y = – 4x² – bx + 5?

365.^· При каком значении b промежуток (–¥; –3] является промежутком убывания функции y = 3x² + bx – 8?

366.^· При каком значении a график квадратичной функции y = ax² + (a – 2)x +  имеет с осью абсцисс одну общую точку?

367.^· · При каких значениях a функция y = 0,5x² – 3x + a принимает неотрицательные значения при всех действительных значениях x?

368.^· · При каких значениях a функция y = –4x² – 16x + a принимает отрицательные значения при всех действительных значениях x?

369.^· · При каком значении c наибольшее значение функции y = –5x² + 10x + c равно –3?

370.^· · При каком значении c наименьшее значение функции y = 0,6x² – 6x + c равно –1?

385.* Пусть x₁ и x₂ — нули функции y = –3x² – (3a – 2)x + 2a + 3. При каких значениях a выполняется неравенство x₁ < –2 < x₂?

386.* Известно, что x₁ и x₂ — нули функции y = 2x² – (3a – 1)x + a – 4, x₁ < x₂. При каких значениях a число 1 принадлежит промежутку [x₁; x₂]?

430.* При каких значениях a данное неравенство выполняется при всех действительных значениях x:

1) x² – 4x + a > 0;

2) x² + (a – 1)x + 1 – a – a² ³ 0;

3) –x² + 5ax – 9a² – 8a < 0;

4) (a – 1)x² – (a + 1)x + a + 1 > 0?

431.* При каких значениях a не имеет решений неравенство:

1) –x² + 6x – a > 0;

2) x² – (a + 1)x + 3a – 5 < 0;

3) ax² + (a – 1)x + (a – 1) < 0?

432.* Для каждого значения a решите систему неравенств:

1)                  2)

433.* Для каждого значения a решите систему неравенств:

1)                  2)

 

Системы уравнений с двумя переменными.

467.* Сколько решений в зависимости от значения a имеет система уравнений:

1)                        3)

2)                    4)

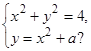
468.* Сколько решений в зависимости от значения a имеет система уравнений:

1)        2)        3)