Подготовка к ОГЭ по математике

В-1

1.      Решите уравнение. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

(−5x +3)(−x +6)=0

2.     Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,07. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо.

3.     Установите соответствие между графиками функций и формулами, которые их задают.

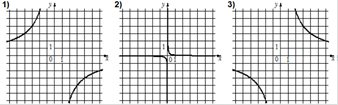А) у=--      Б) у=        В)у=

4.  Площадь четырёхугольника можно вычислить по формуле S=

где d1 и d2 – длины диагоналей четырёхугольника, a – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d1, если  =13, a S=25,5.

5)                   6)

7. 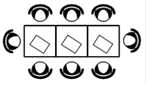 В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 19 квадратных столиков вдоль одной линии?

8. 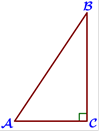 В треугольнике ABC угол C равен 90°, cosB=11/15 , AB = 75 . Найдите BC.

9. В треугольнике ABC угол C равен 90°, tgB=8/5,  BC = 20 . Найдите AC.

10. Синус острого угла A треугольника ABC равен . Найдите cosA .

11. Косинус острого угла A треугольника ABC  Найдите sinA.

12. . В треугольнике ABC известно, что AB = 12,

BC =15 , sin ABC =4/9. Найдите площадь треугольника ABC.

13. 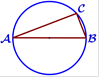Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC,

если угол BAC равен 9°. Ответ дайте в градусах.

В-2

1.     Решите уравнение. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

(x −2)(−2x-3)=0

2.     Вероятность того, что новая шариковая ручка пишет плохо (или не пи-шет), равна 0,19. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо.

3.     Установите соответствие между графиками функций и формулами, которые их задают.

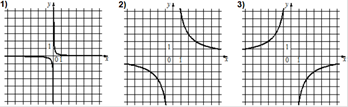А) у=     Б) у=-         В) у=

4.  Площадь четырёхугольника можно вычислить по формуле S=

где d1 и d2 – длины диагоналей четырёхугольника, a – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d1, если  =14, a S=8,75.

5)            6)

7. 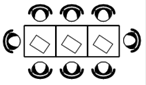 В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 18 квадратных столиков вдоль одной линии?

8. 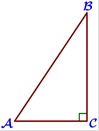 В треугольнике ABC угол C равен 90°, cosB=13/16 , AB = 96 . Найдите BC.

9. В треугольнике ABC угол C равен 90°, tgB=9/7,  BC = 42 . Найдите AC.

10. Синус острого угла A треугольника ABC равен . Найдите cosA .

11. Косинус острого угла A треугольника ABC  Найдите sinA.

12. В треугольнике ABC известно, что AB = 9,

BC =16 , sin ABC =7/12. Найдите площадь треугольника ABC.

13. 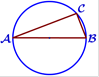Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC,

если угол BAC равен 7°. Ответ дайте в градусах.