Московский государственный университет
имени М. В. Ломоносова

Малый механико-математический факультет

______________________________________________

 

 

 

 

 

 

ПЛОЩАДИ

МНОГОУГОЛЬНИКОВ

 

 

 

 

Методическая разработка

для учащихся заочного отделения

 

 

 

 

 

 

____________________________________________________

 

Москва – 2006

 

 

 

 

 

 

 

 

 

 

Площади многоугольников. Методическая разработка для учащихся заочного отделения Малого механико-математического факультета МГУ.

Автор разработки – Е. Ю. Иванова.

Редакторы – А. В. Деревянкин, Д. А. Калинин.

 

2-е издание, исправленное и дополненное.

1-е издание вышло в 1999 г.

 

§ 1. Основные свойства площадей

Перечислим основные свойства площадей, которые нам будут нуж­ны при решении задач.

А. Площадь плоской фигуры – неотрицательное число.

В. Площади равных фигур равны.

С. Если фигура разрезана на несколько частей, то ее площадь равна сумме площадей этих частей.

D. Площадь квадрата со стороной 1 равна 1.

Используя эти свойства, можно показать, что площадь прямоугольника равна произведению двух его смежных сторон; затем – что площадь параллелограмма равна произведению его основания и высоты; после этого можно получить формулу для площади треугольника.

E. Площадь треугольника равна половине произведения его основания на высоту, опущенную на основание.

Отметим, что это произведение не зависит от того, какую именно сторону и соответствующую ей высоту мы возьмем.

Так как любой многоугольник можно разбить на треугольники, то, используя свойства С и E, мы тем самым можем свести задачу нахождения площади произвольного многоугольника к задаче нахождения площадей нескольких треугольников (разбиение сложной фигуры на треугольники называют триангуляцией).

Замечание. Существование разбиения на треугольники для выпуклого многоугольника очевидно. Можно, например, провести все диагонали, выходящие из одной вершины. Для невыпуклого многоугольника строгое доказательство существования разбиения гораздо сложнее (хотя на первый взгляд возможность такого разбиения может показаться очевидной), поэтому примем тот факт, что любой невыпуклый четырехугольник можно разбить на треугольники, без доказательства.

 

 

 

 

 

§ 2. Разрезания и складывания

В этом параграфе собраны задачи, которые можно решить без вы­числений, проведя лишь простые геометрические построения и исполь­зуя только свойства площадей В и С.

Основной принцип метода "разрезания и складывания" основан на том, что если два многоугольника удается разбить на одинаковые части (такие многоугольники называют равносоставленными), то отсюда вытекает, что площади этих многоугольников равны (фигуры, площади которых равны, называются равновеликими).

Справедлива следующая теорема (доказательство ее выходит за рамки школьной программы).

Теорема. Если два многоугольника равновелики, то один из них можно раз­резать на части, из которых можно составить другой многоугольник.

Обратное утверждение (если два многоугольника равносоставлены, то они равновелики) непосредственно следует из свойств B и С.

Таким образом, два многоугольника равновелики тогда и только тогда, когда они равносоставлены. Это утверждение называется теоре­мой Бойяи-Гервина, а с ее доказательством вы можете познакомиться, например, по книге
В. Г. Болтянского "Равновеликие и равносоставленные фигуры" (22-й выпуск серии "Популярные лекции по математике").

Разбиение фигур на части, из которых потом будут составлены другие фигуры, требует определенной изобретательности. Продемонстрируем этот прием на простых примерах.

Задача 2.1. Докажите, что площадь правильного восьмиугольника равна про­изведению наибольшей и наименьшей из его диагоналей.

Доказательство. Построим для данного восьмиугольника прямоугольник, как изображено на рис. 2.1 (подумайте, как строго выполнить такое построение). Прямоугольник и восьмиугольник равновелики, так как пары прямоугольных треугольников, отмеченные на этом рисунке стрелками, равны (доказательство этого факта оставляем вам в качестве самостоятельного упражнения; проще всего доказать равенство треугольников по катету и гипотенузе).

Большая и меньшая стороны прямоугольника, очевидно, равны наибольшей и наименьшей диагонали восьмиугольника соответственно. Таким образом, площадь прямоугольника, а, значит, и площадь восьмиугольника, равна произведению наибольшей и наименьшей диагоналей восьмиугольника, что и требовалось доказать.

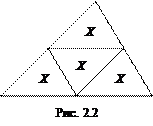Задача 2.2. Докажите, что средняя линия треугольника площади S отсекает от него треугольник площади S/4.

Доказательство. Проведем все средние линии треугольника (рис. 2.2). Они разбивают исходный треугольник на четыре треугольника. Все эти треугольники равны по трем сторонам (средняя линия треугольника равна половине соответствующей стороны, поэтому каждый из треугольников имеет стороны a/2, b/2, c/2, где a, b, c – стороны исходного треугольника). Следовательно, все четыре треугольника имеют одинаковую площадь, которую мы обозначим через X. Сумма их площадей равна 4Х; с другой стороны, она равна S. Таким образом,  Х = S/4, что и требовалось доказать.

Замечание. Предыдущий результат, конечно, можно получить многими другими способами. Этот результат неоднократно пригодится в последующих задачах.

Задача 2.3. Докажите, что площадь трапеции равна произведению одной из боковых сторон на длину перпендикуляра, опущенного на нее из середины другой боковой стороны.

P

Доказательство. Пусть ABCD – данная трапеция с основаниями AD и ВС, точка K – середина стороны CD и KH – перпендикуляр, опущенный на прямую AB. Проведем через точку K прямую, параллельную прямой AB. Пусть М и Р – точки ее пересечения с прямыми AD и ВС соответственно (рис. 2.3). Параллелограмм АВРМ равновелик данной трапеции, так как пятиугольник АВСКМ является для этих двух фигур общим, а треугольники КРC и KMD равны (почему?). Таким образом, параллелограмм и трапеция составлены из одинаковых частей и, следовательно, имеют одинаковые площади. Поскольку площадь параллелограмма равна произведению его основания АВ на высоту KH, то и площадь трапеции равна
АВ · KH, что и требовалось доказать.

Замечание. Доказательство равенства площадей трапеции и параллелограмма более формально можно изложить следующим образом:

S_ABPM = S_ABCKM + S_KPC,

S_ABCD = S_ABCKM + S_KMD,

DKPC = DKMD по стороне и двум прилежащим углам (KC = KD по условию, ÐPKC = ÐMKD как вертикальные, ÐKCP = ÐKDM как внутренние накрест лежащие при параллельных прямых BC и AD и секущей CD),

следовательно, S_KPC = S_KMD, откуда S_ABPM = S_ABCD.

В заключение этого параграфа покажем, как можно доказать мето­дом "разрезания и складывания" теорему Пифагора. Пусть дан квадрат со стороной a + b. Разрежем его так, как показано на рис. 2.4. Получатся два квадрата с длинами сторон a и b и четыре закрашенных прямоугольных треугольника с катетами a и b; обозначим их гипотенузу через c.

Разрежем тот же квадрат так, как показано на рис. 2.5. Полу­чим четыре таких же прямоугольных треугольника, как на рис. 2.4, и квадрат со стороной c (подумайте, как доказать, что это действи­тельно квадрат).

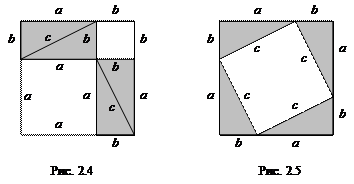Поскольку прямоугольные треугольники на рис. 2.4 и 2.5 равны, то площади незаштрихованных частей на этих рисунках также равны, то есть a² + b² = с², что и требовалось доказать.

 

Задачи к § 2.

2.4           Докажите, что не каждый разносторонний треугольник можно разрезать на два равнобедренных треугольника.

2.5           В трапеции ABCD с основаниями ВС и AD точка K – середина отрезка АВ –соединена с вершинами C и D. Найдите отношение площади треугольни­ка KCD к площади трапеции.

2.6           Через произвольную точку, взятую на диагонали АС параллелограмма ABCD, проведены прямые, параллельные его сторонам. Данный параллело­грамм делится этими прямыми на четыре параллелограмма, два из кото­рых пересекает диагональ АС (рис. 2.6). Докажите, что два других (закрашенных) параллелограмма равновелики.

2.7           В выпуклом четырехугольнике последовательно соединены середины сторон. Найдите отношение площадей полученного и исходного четырехугольников.

2.8           Докажите, что если два выпуклых четырехугольника расположены так, что середины их сторон совпадают (рис. 2.7), то их площади равны.

2.9           Через каждую вершину выпуклого четырехугольника проведе­на прямая, параллельная его диагонали. Точки пересечения этих прямых образуют новый четырехугольник. Докажите, что полученный четырехугольник по площади вдвое больше исходного.

2.10        Произвольная точка плоскости M отражается центрально-симметрично относительно середин сторон некоторого выпуклого четы­рехугольника. Полученные при этом точки являются вершинами нового четырехугольника. Определите его вид и найдите отношение его площа­ди к площади исходного четырехугольника.

2.11        В параллелограмме ABCD проведены четыре отрезка: вершина A соединена с серединой стороны ВС, вершина B – с серединой стороны CD, вершина С – с серединой стороны DA, а вершина D – с серединой стороны AB. Докажите, что четырехугольник, образуемый этими четырьмя отрезками (рис. 2.8), – параллелограмм, и что его площадь в пять раз меньше площади паралле­лограмма ABCD.

             Указание. Посмотрите на рис. 2.8 и подумайте, как из девяти частей, на которые разрезан исходный параллелограмм, сложить пять одинаковых параллелограммов.

2.12        Каждая из трех прямых делит площадь многоугольника пополам (рис. 2.9). Докажите, что пло-щадь треугольника, образованного этими прямыми, меньше 1/4 площади многоугольника.

2.13        Через вершины C и D квадрата ABCD проведены параллельные прямые, пересекающие продолжение стороны АВ в точках Е и Н соответственно. Из точек D и Н опущены перпендикуляры DF и HG на прямую СЕ (рис. 2.10). Докажите, что квадрат ABCD равновелик прямоугольнику DFGH.

§ 3. Соотношения между
элементами треугольника

При решении геометрических задач треугольники играют существенную роль. Различные элементы многоугольников и их площадь можно найти, разбивая их на треугольники и проводя вычисления для отдельных треугольников. По­этому очень полезно знать различные выражения, связывающие элементы треуголь­ника. Мы приведем несколько формул; некоторые из них вам знакомы, а некоторые, вероятно, вы увидите впервые. Полезно помнить основные из этих формул и уметь все их доказывать.

Во всех формулах параграфа, если отдельно не оговорено иного, будем для произвольного треугольника АВС использовать следующие обозначения:

·       а, b и с – соответственно стороны BC, AC и AB,

·       р – полупериметр,

·       r – радиус вписанной окружности,

·       R – радиус описанной окружности,

·       S – площадь треугольника АВС,

·       r_a, r_b, r_c – радиусы вневписанных окружностей (на рис. 3.1 изображена вневписанная окружность радиуса r_a, касающаяся стороны а и продолжений сторон b, c).

·       h_a, h_b, h_c – высоты, опущенные на стороны a, b и c соответственно,

·       m_a, m_b, m_c – медианы, исходящие из вершин A, B и C соответственно,

·       l_a, l_b, l_c – биссектрисы, исходящие из вершин A, B и C соответственно.

Начнем с хорошо известных вам теорем.

Теорема косинусов. В любом треугольнике

c² = a² + b² – 2ab × cos ÐC.

Обобщенная теорема синусов. В любом треугольнике

Отметим, что равенство  называется обычной теоремой синусов.

Приведем теперь 14 формул, выражающих площадь треугольника через различные элементы треугольника и радиусы его вписанной, описанной и вневписанных окружностей.

1.       ,

2.       ,

3.       ,

4.       S = pr,

5.       S = r_a × (p – a),

6.        

(формула Герона),

7.       ,

8.       ,

9.       ,

10.    ,

11.    ,

12.    S = 2R² × sin ÐA × sin ÐB × sin ÐC,

13.    ,

14.    .

Формулы 1 – 4 и 6 были доказаны в курсе геометрии.

Формула 5 до­казывается аналогично формуле 4. Действительно, если O – центр вневписанной окружности (рис. 3.1), то

S_ABC = S_OAB + S_OAC – S_OBC = .

Подставив в формулу Герона выражения для p – a, p – b, p – c через площадь треугольника и радиусы вневписанных окружностей, полученные из формулы 5, можно вывести формулу 7; если же еще подставить в формулу Герона выражение для p из формулы 4, то получится формула 8.

Чтобы получить формулу 9, необходимо воспользоваться тождеством
(p – b) + (p – c) = a; выразив p – b и p – c при помощи формулы 5 через площадь треугольника и радиусы вневписанных окружностей, после несложных преобразований получим требуемый результат.

Формулу 10 можно получить из формулы 5, если заме­тить, что AD = р, где D – точка касания вневписанной окружности с продолжением стороны AB (докажите это равенство самостоятельно), откуда

.

Из последнего равенства вытекает также равносильность формул 7 и 14.

Наибольшую сложность, вероятно, представляет доказательство формулы 11. Возможен следующий путь: сперва следует выразить cos ÐA через стороны треугольника при помощи теоремы косинусов. Зная cos ÐA, можно при помощи формулы двойного угла доказать, что   Выразив аналогичным образом синусы двух других половинных углов, подставив их в выражение  и проведя преобразования, можно убедиться в том, что оно в точности равно S.

Формулы 12 и 13 могут быть получены из формулы 3 с помощью обобщенной теоремы синусов.

Упражнение 3.1. Проведите подробные доказательства формул 5, 7 – 14.

Упражнение 3.2. В треугольнике даны стороны a, b, c. Найдите

а) cos ÐA;             б) r;                        в) R;      

г) h_a;                      д) m_a;                     е) l_a.

c

b

Решение упражнения 3.2(д). Проведем в треугольнике ABC медиану AD (рис. 3.2); пусть ÐADB = a, тогда ÐADC = p – a.

Воспользуемся дважды теоремой косинусов.

a/2

a/2

Для DABD: c² = (a/2)²  + m_a² – 2·(a/2)·m_a cos a.

Для DACD: b² = (a/2)²  + m_a² – 2·(a/2)·m_a cos  (p – a).

Сложим полученные равенства и учтем, что cos a = – cos (p – a):

.

Извлекая квадратный корень из обеих частей равенства, получим окончательный ответ.

Ответ: .

Также полезно знать некоторые формулы для элементов прямоугольного треугольника. Пусть катеты прямоугольного треугольника равны a и b, гипотенуза – c. Тогда имеют место следующие соотношения:

15.    (центр описанной окружности – середина гипотенузы),

16.    .

Упражнение 3.3. Докажите формулы 15 и 16.

Упражнение 3.4. В прямоугольном треугольнике даны катеты a и b. Найдите

а) sin ÐA;                      б) h_c;                      в) m_a и m_с;                        г) l_a и l_с.

Приведем несколько примеров решения задач с использованием формул площади треугольника.

Задача 3.1. Докажите, что в равнобедренном треугольнике сумма расстояний от любой точки основания до боковых сторон равна высоте треуголь­ника, опущенной на его боковую сторону.

Доказательство. Случай, когда данная точка M совпадает с вершиной A или B, тривиален. Рассмотрим случай, когда M не совпадает с вершинами основания. Пусть длина боковой стороны данного треуголь­ника равна а, длина высоты, опущенной на нее, равна h, расстояния от точки M до боковых сторон равны h₁ и h₂ (рис. 3.3).

Отрезок CM делит треугольник ABC на два треугольника. Запишем равенство площадей:

S_ABC = S_AMC + S_BMC,

или

,

откуда h₁ + h₂ = h, что и требовалось доказать.

Задача 3.2 (теорема о биссектрисе). Пусть ВН – биссектриса угла B треугольника ABC. Докажите, что АН : НС = АВ : ВС.

Доказательство. Пусть ÐB = 2a. Тогда (рис. 3.4)

.

С другой стороны,

,

где h – высота треугольника ABC, опущенная из вершины B. Приравнивая правые части полученных равенств, имеем: АН : НС = АВ : ВС, что и требовалось доказать.

Задача 3.3. Трапеция ABCD (BC и AD – основания) вписана в окружность. На дуге CD взя­та точка M и соединена со всеми вершинами трапеции. В треугольнике CMD извес­тен угол CMD, равный b, в треугольнике ABM известна разность углов ABM и BAM, равная a. Найдите отношение радиуса r вписанной в треугольник ABM окружности к полупериметру p треугольника ABM.

Решение. Найдем в треугольнике ABM все углы. Обозначим ÐBAM = a, ÐABM = b, ÐBMA = g (рис. 3.5). По условию b – a = a. Из свойств вписанных углов следует, что угол a измеряется половиной дуги ВСМ, угол b – половиной дуги ADM, угол CMD = b – полу­суммой дуг АВ, ВС и AD. Трапеция, вписанная в окружность, является равнобедренной; следовательно, дуги АВ и CD равны. Таким образом, a + b = b (проверьте, что как угол a + b, так и угол b измеряется половиной дуги BMA). Тогда из равенств b – a = a, b + a = b имеем:

, ;

также g = 180° – (a + b) = 180° – b.

Применив формулы 4 и 14 к треугольнику ABM, получаем:

.

Ответ: .

 

Задачи к § 3.

3.4.         Даны два треугольника ABC и A₁B₁C₁, причем известно, что AB > A₁B₁, AC > > A₁C₁, BC > B₁C₁. Верно ли, что площадь треугольника ABC больше площади треугольника A₁B₁C₁?

3.5.         В треугольнике ABC медианы AM и BK перпендикулярны. Найдите площадь треугольника, если AM = m, BK = k.

3.6.         В выпуклом четырехугольнике ABCD точки M, N, K, L – середины сторон AB, BC, CD, DA соответственно. В четырехугольнике MNKL точки P, Q, R, S – середины сторон MN, NK, KL, LM соответственно. Известно, что MN = NK, а  ÐMNK = 30°. Найдите площадь четырехугольника PQRS, если AC = a.

3.7.         Докажите, что существует треугольник, сторонами которого являются медианы заданного произвольного треугольника. Найдите его площадь, если площадь исходного треугольника равна S.

3.8.         Докажите, что площадь многоугольника, описанного около ок­ружности, равна половине произведения радиуса этой окружности на периметр многоугольника: S = pr.

3.9.         Докажите, что сумма расстояний от произвольной точки, ле­жащей внутри правильного треугольника или на его границе, до его сто­рон равна высоте треугольника.

             Замечание. Аналогично можно доказать и более общую теорему: сумма расстояний от произвольной точки, лежащей внутри правильного n-угольника или на его границе, до его сторон равна апофеме, умноженной на количество сторон (апофема – расстояние от центра правильного многоугольника до любой из его сторон; оно равно радиусу окружности, вписанной в этот многоугольник).

3.10.      Отрезки MN и PQ делят стороны AD и BC выпуклого четырехугольника ABCD на три равные части (рис. 3.6). Докажите, что площадь четырехугольника MNQP составляет треть от площади четырехугольника ABCD.

Замечание. Верно и более общее утверждение: если n – 1 прямая делит каждую из двух противоположных сторон выпуклого четырехугольника на n равных частей, то площади n получившихся четырехугольников образуют арифметическую прогрессию.

3.11.      Точки E и K – середины сторон BC и AD выпуклого четырехугольника ABCD. Докажите, что площадь треугольника AED равна сумме площадей треугольников ABK и KCD.

3.12.      В прямоугольном треугольнике ABC катеты AC и BC равны b и a соответственно; h – длина высоты CC₁; r – радиус окружности, вписанной в треугольник ABC; r₁ и r₂ – радиусы окружностей, вписанных соответственно в треугольники ACC₁ и BCC₁.  Докажите, что

а) r + r₁ + r₂ = h;                                 б) .

3.13.      Докажите для произвольного треугольника следующие соотношения:

а) ;                                  б) ;

в)  r_ar_b + r_br_c + r_cr_a = p²;                    г)  r_a + r_b + r_c = 4R + r.

§ 4. Отношения площадей

Очень часто при решении геометрических задач приходится нахо­дить, как связаны площади тех или иных фигур. В § 2 мы разобрали один из методов, при помощи которого это можно сделать. Но для того, чтобы установить связь двух площадей, вовсе не обязательно разрезать и складывать фигуры. Например, очень часто бывает удобно сравнивать площади двух треугольников, используя свойство E из § 1. Приведем некоторые очевидные следствия из этого свойства.

Утверждение 1. Если вершину треугольника передвигать по прямой, параллельной его основанию, то его площадь при этом не меняется.

Поясним это утверждение на примере. Возьмем две параллельные прямые и на одной из них отметим отрезок AB, на другой – произвольные точки C, D и E (рис. 4.1). Тогда треугольники АВС, ABD и ABE будут иметь одинаковые площади, так как у них общее основание АВ и равные высоты, опущенные на это основание.

Задача 4.1. Пусть O – точка пересечения отрезков АС и BD (рис. 4.2). Докажите, что для того, чтобы площади треугольников AOB и COD были равны, необходимо и достаточно, чтобы прямые ВС и AD были параллельны.

Замечание. Для того, чтобы решить эту задачу, нужно доказать два утверждения:

1. Если прямые ВС и AD параллельны, то площади тре­угольников АОВ и COD равны;

2. Если площади треугольников АОВ и COD равны, то прямые ВС и AD параллельны.

Вообще, если нужно доказать утверждение "для того, чтобы вы­полнялось А, необходимо и достаточно, чтобы выполнялось В", то требуется доказывать два утверждения:

1. Если выполняется А, то выполняется B;

2. Если выполняется В, то выполняется А.

Иногда вместо фразы "для того, чтобы вы­полнялось А, необходимо и достаточно, чтобы выполнялось В" говорят "А выполняется тогда и только тогда, когда выполняется В" или "утверждения A и В равносильны". Все эти формулировки эквивалентны.

Решение задачи 4.1. Докажем оба сформулированных утверждения.

1. Пусть прямые ВС и AD параллельны. По утверждению 1 имеет место равенство S_ABD = S_AСD, тогда S_AOB = S_ABD – S_AOD =  S_ACD – S_AOD = S_COD.

2. Пусть S_AOB =S_COD. Тогда S_ABD = S_AOB + S_AOD =  S_COD + S_AOD = S_AСD. Треугольники ABD и ACD имеют общее основание AD; значит, высоты, опущенные на прямую AD из точек B и C, также равны, откуда следует, что прямые AD и ВС параллельны, что и требовалось доказать.

Утверждение 1 можно сформулировать в более общем виде.

Утверждение 2. Пусть дан отрезок АВ. Геометрическое место точек M таких, что площадь треугольника АВМ равна заданной величине S, есть две прямые, параллельные отрезку АВ и находящиеся от прямой AB на расстоянии h = 2S/AB.

Замечание. Для того, чтобы доказать сформулированное выше ут­верждение, надо доказать два утверждения:

1. Если точка M такова, что S_ABM = S, то она лежит на одной из указан­ных прямых;

2. Если точка M лежит на одной из указан­ных прямых, то S_ABM = S.

Контрольный вопрос 4.1. Дан отрезок AB. Что представляет собой множество точек M, для которых площадь треугольника ABM меньше за­данной величины S? больше S? Изобразите эти множества на рисунке разным цветом.

Приведем еще одно утверждение, связывающее площади треугольников.

Утверждение 3. Если треугольники имеют одинаковые высоты, то отношение их площадей равно отношению оснований (сторон, на которые опущены высоты).

В пару к этому утверждению можно добавить еще одно.

Утверждение 4. Если треугольники имеют одинаковые основа­ния, то отношение их площадей равно отношению высот, опущенных на основание.

Упражнение 4.1. Докажите, что медиана треугольника делит его на две равнове­ликие части.

Упражнение 4.2. Докажите, что медианы треугольника делят его на шесть равнове­ликих частей.

Покажем, как можно применять приведенные утверждения к решению задач.

Задача 4.2. В треугольнике ABC на продолжении стороны AB выбрана точка K так, что AB = BK, а на стороне АС – точка P так, что AP : PC = 1:2. Найдите площадь треугольника APK, если площадь треугольника ABC равна 1.

Решение. Рассмотрим вспомогательный треугольник AKC (рис. 4.3). Треугольники АВС и AKC имеют общую высоту, опущенную из точки C, следовательно,

Значит, S_AKC = 2.

Треугольники AKC и AKP имеют общую высоту, опущенную из вершины K, следовательно,

Следовательно, S_AKP = S_AKC/3 = 2/3.

Ответ: 2/3.

На данном примере мы, фактически, доказали частный случай сле­дующего утверждения.

Утверждение 5. Если два треугольника имеют общий угол, то их площади относятся как произведения сторон, заключающих этот угол.

Доказательство этого утверждения полностью аналогично реше­нию предыдущей задачи. Из него можно получить следствие, связывающее площади подобных треугольников.

Утверждение 6. Если два треугольника подобны с коэффициен­том k (стороны одного в k раз больше сторон другого), то их площади относятся с коэффициентом k² (площадь одного в k² раз больше площади другого).

Например, средняя линия треугольника отсекает от него треугольник, площадь которого в 4 раза меньше, чем у исходного треугольника (этот факт уже был доказан выше другим способом).

Замечание. Утверждение 5 проще было бы доказать иначе, при помощи формулы площади треугольника: S = 0,5×ab×sin ÐC, где а и b – две стороны треугольника, а C – угол, заключенный между этими сторонами. Однако и приведенное решение задачи 4.2 представляет из себя определенный интерес.

Разберем несколько примеров.

Задача 4.3. Пусть диагонали выпуклого четырехугольника делят его на четыре треугольника, площади которых равны S₁, S₂, S₃, S₄ (рис. 4.4). Докажите, что S₁×S₃ = S₂×S₄.

Доказательство. Согласно утверждению 3

S₁ : S₄ = S_АОВ : S_AOD = BO : OD,

S₂ : S₃ = S_COB : S_COD = BO : OD.

Следовательно, S₁ : S₄ = S₂ : S₃, откуда S₁×S₃ = S₂×S₄, что и требовалось доказать.

Рассмотренная задача известна под названием «теорема о бабочках».

Задача 4.4. В выпуклом четырехугольнике ABCD середина диагонали АС со­единена с серединами сторон АВ и AD. Докажите, что площадь получен­ного четырехугольника в 4 раза меньше площади ABCD.

Доказательство. Пусть ABCD – данный четырехугольник, а точка O – середина диагонали АС. Точки M и K – середины сторон АВ и AD соответственно (рис. 4.5).

В треугольнике АВС отрезок ОМ – средняя линия, следовательно, S_АМО = S_АВС/4.

Аналогично, S_АKО = S_АDС/4.

Значит, S_AMOK = S_АМО + S_АKО = S_ABC/4 + S_ADC/4 = = S_ABCD/4, что и требовалось доказать.

Замечание. Отметим также, что если вместо середины диагонали выбрать внутри четырехугольника ABCD произвольную точку T так, что прямая ОТ параллельна диа­гонали BD, то площадь четырехугольника АМТК будет также равна чет­вертой части площади четырехугольника ABCD. Попробуйте доказать этот факт самостоятельно.

В заключение покажем, как с помощью утверждения 6 можно по­лучить еще одно доказательство теоремы Пифагора.

Доказательство. Пусть прямоугольный треугольник ABC имеет катеты a и b и гипотенузу c. Опустим из вершины прямого угла С высоту. Она разбивает данный треугольник на подобные ему (и друг другу) прямоугольные треугольники. Пусть площади этих треугольников равны S₁ и S₂, а площадь исходного треугольника – S (рис. 4.6). Коэффициент подобия равен отношению соответствующих сторон. В силу утверждения 6 имеем:

,    .                              (1)

Из равенства S₁ + S₂ = S получаем: S₁/S + S₂/S = 1. Подставляя в это равенство соотношения (1), имеем: b²/c² + a²/c² = 1, откуда a² + b² = c², что и требовалось доказать.

Задачи к § 4.

4.5         Ответьте на контрольный вопрос 4.1 из § 4.

4.6           Докажите, что выпуклый четырехугольник является паралле­лограммом тогда и только тогда, когда каждая из диагоналей делит его площадь пополам.

4.7           Прямая, параллельная диагонали АС выпуклого четырехугольника ABCD и проходящая через середину его диагонали BD, пересекает сторону AD в точке E. Докажите, что прямая ЕС делит площадь четырехугольника ABCD пополам.

4.8           Точка A₁ лежит на стороне ВС треугольника АВС, а точка C₁ – на его стороне АВ, причем отрезки AA₁ и СС₁ пересекаются в точке О. Известно, что площади треугольников A₁OC, СОА и AOC₁ равны S₁, S₂, S₃ соответственно. Найдите площадь треугольника A₁BC₁.

4.9           а) На продолжении стороны ВС выпуклого четырехугольника ABCD найдите такую точку O, чтобы площадь ABCD равнялась площа­ди треугольника АВО. Не забудьте указать все возможные решения задачи.

             б) Как, используя результат пункта (а), превратить любой выпук­лый многоугольник в равновеликий ему, но имеющий на одну сторону меньше?

4.10        В треугольнике АВС на медиане ВМ взята точка K так, что BK : KM = 1:2. Найдите отношение площадей треугольников ABK и АВС.

4.11        Через середину высоты, опущенной на основание равнобедренного треугольника, прове­дены две прямые, соединяющие ее с вершинами основания. Какую часть площади исходного треугольника составляет каждая из 6 частей, на ко­торые эти прямые разбивают треугольник?

4.12        На диагонали BD параллелограмма ABCD взята точка M, на отрезке MC – точка P, на стороне BC – точка K (рис. 4.7). Известно, что S_ABCD = 1, BM : MD = 2:1, MP : PC = 1:2, BK = KC. Найдите площадь четырехугольника ВКРМ.

4.13        Диагонали делят трапецию на четыре треугольника. Пусть S₁ и S₂ – площади треугольников, прилегающих к основаниям. Найдите площадь трапеции.

4.14        Каждая вершина параллелограмма соединена с серединами двух противоположных сторон. Какую часть площади параллелограмма составляет площадь фигуры, ограниченной проведенными линиями (рис. 4.8)?

4.15        Через середину каждой диагонали выпуклого четырехуголь­ника проведена прямая, параллельная другой его диагонали. Точка пере­сечения этих прямых соединена отрезками с серединами сторон четырех­угольника. Докажите, что эти четыре отрезка делят данный четырех­угольник на четыре равновеликие части.

4.16        В треугольнике АВС продолжили сторону АВ за вершину B отрезком ВР таким, что BP = AB, сторону AC – за вершину A отрезком AM таким, что АМ = СА, сторону ВС – за вершину C отрезком CK таким, что CK = ВС. Во сколько раз площадь полученного треугольника PMK больше площади треугольника АВС?

             Указание. Соедините точки B и M, Р и C, А и K.

4.17        Через точку, взятую внутри треугольника, проведены три прямые, параллельные его сторонам. Эти прямые делят треугольник на 6 частей, три из которых – треугольники с площадями S₁, S₂ и S₃. Найдите площадь исходного треугольника.

4.18        Дан выпуклый четырехугольник ABCD. Найдите геометриче­ское место точек M таких, что площади многоугольников ABCD и АВСМ равны.

4.19        Точки M, P и K расположены соответственно на сторонах АВ, ВС и СА треугольника АВС так, что 3×АМ = АВ, 3×ВР = ВС, 3×CK = CA. Найдите площадь треугольника, ограниченного прямыми АР, ВК и CM, если площадь треугольника АВС равна S.

4.20        На сторонах выпуклого четырехугольника ABCD взяты точки М, Р, К, Н соответственно так, что АМ : МВ = 3:5, ВР : РС = 1:3, CK : KD = 4:5,
DH : HA = 1:8. Найдите отношение площади шестиугольника MBPKDH к площади че­тырехугольника ABCD.

 

§ 5. Теоремы Чевы и Менелая

Для решения задач часто требуется находить отношения, в которых делятся те или иные отрезки. В этом помогают несколько сильных фактов, к которым относятся теоремы Чевы и Менелая. Прежде чем сформулировать и доказать эти теоремы, рассмотрим лемму (вспомогательное утверждение).

Лемма 5.1. Дан произвольный треугольник ABC; точка B₁ лежит на стороне AC, E – произвольная точка отрезка BB₁ (рис. 5.1). Тогда

S_ABE : S_CBE = AB₁ : B₁C.

Доказательство. Из свойств площадей следует, что

,  Þ

Þ ,

что и требовалось доказать.

Примечание. При решении было использовано следующее свойство пропорции: если  и то .

Замечание. Утверждение леммы 5.1 будет верным и в случае, когда точка E лежит на продолжении отрезка BB₁ за точку B₁. Подумайте, как изменится доказательство в этом случае.

Таким об­разом, отношение площадей треугольников ABE и СBЕ не зависит от выбора точки Е и зависит только от выбора точки B₁ на стороне АС.

Теорема Чевы. Пусть точка А₁ лежит на стороне ВС треуголь­ника АВС, точка B₁ – на стороне АС, а точка С₁ – на стороне AB. От­резки AA₁, BB₁ и CC₁ (называемые также чевианами) пересекаются в одной точке тогда и только тогда, когда

.

Доказательство.

Необходимость. Пусть отрезки AA₁, BB₁ и CC₁ пересекаются в одной точке Е (рис. 5.2). Тогда, согласно лемме 5.1, имеем:

, , .

Перемножая эти равенства, получим:

,

что и требовалось доказать.

Достаточность. Пусть точки A₁, B₁ и C₁ таковы, что

.                               (1)

Докажем, что тогда отрезки AA₁, BB₁ и CC₁ пересекаются в одной точке.

Предположим, это не так: отрезки AA₁ и BB₁ пересекаются в точке Е, а отрезок CC₁ не про­ходит через точку Е. Пусть прямая СЕ пересекает сторону AB в точке C₂ (рис. 5.3). Тогда по доказанному выше для чевиан AA₁, BB₁ и CC₂ выполнено условие

.                               (2)

Из (1) и (2) следует, что AC₂ : C₂B = AC₁ : C₁B, то есть точки C₁ и С₂ делят отрезок AB в одинаковом отношении. Это означает, что точки C₁ и С₂ совпадают, что противоре­чит нашему предположению. Следовательно, оно неверно и отрезки AA₁, BB₁ и CC₁ пересекаются в одной точке, что и требовалось доказать.

 

Теорема Менелая. Пусть точка A₁ лежит на стороне ВС тре­угольника АВС, точка В₁ – на стороне АС, а точка C₁ – на продолжении стороны AB. Точки A₁, B₁ и C₁ лежат на одной прямой тогда и только тогда, когда

.

Доказательство.

Необходимость. Пусть точки A₁, B₁ и C₁ лежат на одной прямой. Проведем отрезки AA₁ и CC₁ и введем обозначения для площадей получившихся треугольников, как показано на рис. 5.4. Тогда по лемме 5.1

.

Кроме того, из формул площадей треугольников следует, что

, .

Перемножая эти равенства, получим:

,

что и требовалось доказать.

Необходимость. Доказательство аналогично дока­зательству второй части теоремы Чевы. Проведите его самостоятельно.

Комментарий к теоремам Чевы и Менелая. В действительности верны и более общие утверждения, чем содержащиеся в этих двух теоремах. Так, в теореме Чевы точки A₁, B₁ и C₁ не обязаны лежать внутри сторон: утверждение теоремы остается верным, если одна точка лежит на стороне, а две другие – вне сторон треугольника. Аналогично, теорема Менелая остается верной, если все три точки A₁, B₁ и C₁ лежат на продолжениях соответствующих сторон. Докажите самостоятельно теоремы Чевы и Менелая для этих случаев расположения точек. Для этого необходимо немного изменить доказательства, приведенные выше.

Упражнение 5.1. Докажите с помощью теоремы Чевы, что в любом треугольнике

а) медианы;

б) биссектрисы;

в) прямые, содержащие высоты

пересекаются в одной точке.

Замечание. При решении пункта (в) не забудьте отдельно рассмотреть случаи прямоугольного и тупоугольного треугольника!

Рассмотрим пример задачи на применение теоремы Менелая.

Задача 5.1. Точки B₁ и C₁ лежат соответственно на сторонах AC и AB треугольника ABC и делят эти стороны в отношениях BC₁ : C₁A = p и CB₁ : B₁A = q; E – точка пересечения отрезков BB₁ и CC₁. Найдите отношение CE : EC₁.

Решение. Применим теорему Менелая для треугольника ACC₁ и точек B₁, E и B (рис. 5.5):

.

Из условия задачи следует, что

.

Кроме того, ; исходя из этого, получаем искомое отношение:

Ответ: CE : EC₁ = q × (p + 1) / p.

Сформулируем аналогичную задачу. Решите ее самостоятельно.

Упражнение 5.2. Точки B₁ и C₁ лежат соответственно на сторонах AC и AB треугольника ABC; E – точка пересечения отрезков BB₁ и CC₁. Найдите отношение AC₁ : C₁B, если B₁E : EB = p и CB₁ : B₁A = q.

 

Задачи к § 5.

5.2.         Внутри треугольника АВС лежит точка M. Докажите, что пло­щади треугольников ABM и CBM равны тогда и только тогда, когда точ­ка M находится на медиане BK.

5.3.         Стороны треугольника равны a, b, c. Найдите отношение, в котором

а) биссектриса l_b делит биссектрису l_a;

б) высота h_b делит высоту h_a (в этом пункте треугольник предполагается остроугольным).

5.4.         Дан треугольник ABC, в котором BM – медиана. Точка P лежит на стороне AB, точка Q – на стороне BC, причем AP : PB = 2 : 5, BQ : QC = 6. Отрезок PQ пересекает медиану BM в точке R. Найдите отношение BR : RM. (Ткачук, стр. 289)

5.5.         В треугольнике ABC угол C – прямой, BC = 3, AC = 4, CD – биссектриса, AM – медиана. Найдите площадь треугольника CEM, где E – точка пересечения отрезков CD и AM.

5.6.         Докажите, что если внутри выпуклого четырех(Ткачук, стр. 289)угольника ABCD найдется такая точка O, что отрезки OA, OB, OC и OD делят его на четыре равновеликие части, то хотя бы одна из диагоналей этого четырехугольника делит другую диагональ пополам.

5.7.         Пусть точка А₁ лежит на стороне ВС треуголь­ника АВС, точка B₁ – на стороне АС, а точка С₁ – на стороне AB. От­резки AA₁, BB₁ и CC₁ пересекаются в одной точке O. Обозначим площади треугольников AOC₁, C₁OB, BOA₁, A₁OC, COB₁, B₁OA через S₁, S₂, S₃, S₄, S₅, S₆ соответственно. Докажите, что

а) S₁ × S₃ × S₅ = S₂ × S₄ × S₆;

б) , , (теорема Ван-Обеля);

в) ;                  г) .

5.8.         На сторонах AB, BC, CA треугольника ABC отмечены соответственно точки C₁, A₁, B₁ – точки касания вписанной окружности. Докажите, что отрезки AA₁, BB₁ и CC₁ пересекаются в одной точке.

5.9.         На сторонах AB, BC, CA треугольника ABC отмечены соответственно точки C₁, A₁, B₁ – точки касания вневписанных окружностей. Докажите, что отрезки AA₁, BB₁ и CC₁ пересекаются в одной точке.

             Указание. Докажите и используйте тот факт, что каждая точка касания вневписанной окружности делит периметр треугольника пополам. То есть, например, AB + BA₁ = AC + CA₁.

5.10.      На стороне BC треугольника ABC отмечена точка A₁, отличная от середины. Возьмем любую точку Z на отрезке AA₁. Пусть B₁ – точка пересечения луча BZ со стороной AC; С₁ – точка пересечения луча СZ со стороной AB. Докажите, что все прямые B₁C₁, полученные таким образом (для всевозможных точек Z), пересекаются в одной точке.

5.11.      Теорема Дезарга. Треугольники ABC и A₁B₁C₁ с попарно непараллельными сторонами расположены так, что прямые AA₁, BB₁ и CC₁ пересекаются в одной точке. Точки M, K, P – точки пересечения прямых AB и A₁B₁, BC и B₁C₁, AC и A₁C₁ соответственно. Докажите, что  M, K, P лежат на одной прямой.

Замечание. В этой задаче возникает большое количество различных случаев в зависимости от взаимного расположения перечисленных в условии точек. В частности, некоторые из этих точек могут совпадать. Постарайтесь рассмотреть все возможные варианты!

 

§ 6. Геометрические неравенства

Задачи на геометрические неравенства (т.е. задачи, в которых требуется сравнить какие-либо величины или доказать неравенство) достаточно редки, но, как правило, решение их вызывает большое количество трудностей. Элементы таких задач встречаются на вступительных экзаменах в сильные математические вузы – например, в ситуациях, когда для правильного построения чертежа к геометрической задаче необходимо сравнить какие-либо величины.

Простейшими из задач на геометрические неравенства можно считать те, которые решаются при помощи неравенства треугольника. Основные приемы решения таких задач были разобраны в брошюре «Планиметрия». Кроме неравенства треугольника, часто применяется также теорема о соотношении сторон и углов в треугольнике.

Теорема. В любом треугольнике напротив большей стороны лежит больший угол; обратно, в любом треугольнике напротив большего угла лежит бóльшая сторона.

Рассмотрим пример применения этой теоремы.

Задача 6.1. В треугольнике ABC серединный перпендикуляр к стороне BC пересекает сторону AB в точке D и продолжение стороны AC в точке E. Докажите, что AE > AD.

Решение. Обозначим середину стороны BC через M. Треугольник CBD – равнобедренный (почему?). Следовательно, DM является биссектрисой этого треугольника: ÐCDM = ÐMDB = ÐADE (рис. 6.1). Угол CDM – внешний для треугольника CED, поэтому ÐCDM = ÐAED + ÐACD. Следовательно, ÐADE = ÐCDM > ÐAED, а поскольку напротив большего угла треугольника ADE лежит бóльшая сторона, то AE > AD, что и требовалось доказать.

C

Задача 6.2. На сторонах угла A взяты точки B и C. Через середину K отрезка BC проведена прямая, пересекающая стороны угла AB и AC в точках D и E соответственно. Докажите, что площадь треугольника ADE больше площади треугольника ABC.

Решение. Проведем через точку B прямую, параллельную AC. Пусть она пересекает прямую DE в точке F (рис. 6.2). Точка F обязательно будет лежать внутри отрезка KD (почему?). Заметим, что треугольники BKF и CKE равны по стороне (BK = CK) и двум прилежащим углам (углы при вершине K равны как вертикальные, а ÐKBF = ÐKCE как внутренние накрест лежащие при параллельных прямых и секущей). Из равенства треугольников следует и равенство их площадей; тогда S_BKD = S_BKF + S_BFD > S_BKF = S_CKE, и S_ADE = S_ABKE + S_BKD >
> S_ABKE + S_CKE = S_ABC, что и требовалось доказать.

Задача 6.3. Пусть a, b, c, d – длины последовательных сторон выпуклого четырехугольника, S – его площадь. Докажите, что

Решение. Обозначим данный четырехугольник через ABCD так, чтобы a = AB, b =
= BC, c = CD, d = DA. Тогда:

 

что и требовалось доказать.

 

Задачи к § 6.

6.4.         В прямоугольной трапеции ABCD с основаниями AB и CD и прямым углом A сравните периметры треугольников ABC и CDB.

6.5.         Через данную внутри угла A точку K проведите при помощи циркуля и линейки прямую, пересекающую стороны угла в точках B и C так, чтобы площадь треугольника ABC была наименьшей.

Замечание. Стандартные построения, известные из школьного курса (построение параллельных и перпендикулярных прямых, откладывание равных отрезков и т.п.) считаются известными; эти построения можно использовать, не описывая их выполнение подробно.

6.6.         В трапеции ABCD с основаниями AB и CD на диагонали AC берется точка P и через нее проводится прямая MN, параллельная основанию AB (точка M лежит на стороне AD, N – на стороне BC). Как нужно выбрать точку P, чтобы сумма площадей треугольников APM и CPN была наименьшей?

             Указание. Докажите, что если P – точка пересечения диагоналей трапеции, то MP = PN.

6.7.         Мальчик и девочка делят треугольный торт следующим образом. Мальчик выбирает произвольную точку внутри торта, а девочка проводит через эту точку разрез и забирает больший из двух получившихся кусков. Каждый из ребят хочет получить по возможности бóльшую часть торта. Докажите, что мальчику выгоднее всего указывать точку пересечения медиан треугольника.

6.8.         а) Докажите, что сумма расстояний от произвольной точки, взятой внутри неравностороннего треугольника, до его сторон заключена между длинами наибольшей и наименьшей высот этого треугольника.

             б) В треугольнике ABC выполняется следующее соотношение: AB > BC >
> AC. Найдите внутри треугольника или на его границе точку, сумма расстояний от которой до прямых AB, AC и BC минимальна.

6.9.         Докажите, что если последовательно соединить отрезками середины сторон произвольного выпуклого

                а) пятиугольника;

                б) шестиугольника;

                в) n-угольника (n > 6),

             то площадь полученного многоугольника составит более половины площади исходного.

6.10.      Пусть a, b, c, d – длины последовательных сторон выпуклого четырехугольника, S – его площадь. Докажите, что  причем равенство имеет место тогда и только тогда, когда четырехугольник является вписанным, а его диагонали перпендикулярны.

6.11.      Периметр четырехугольника равен 4. Докажите, что его площадь не превосходит 1.

Оглавление

 

§ 1. Основные свойства площадей                                                                               3

§ 2. Разрезания и складывания                                                                                      4

§ 3. Соотношения между элементами треугольника                                              8

§ 4. Отношения площадей                                                                                              14

§ 5. Теоремы Чевы и Менелая                                                                                       20

§ 6. Геометрические неравенства                                                                                 25