Разбор заданий  "Определение вероятности" Пример 1

В среднем из 2000 садовых насосов, поступивших в продажу, 12 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.

Решение:

2000 – 12 = 1988 – количество насосов, которые не подтекают

Событие А = «выбранный насос не подтекает». Значит, N(A) = 1988, N = 2000

Ответ: 0,994.

Пример 2

Фабрика выпускает сумки. В среднем на 154 качественные сумки приходится 16 сумок, имеющих скрытые дефекты. Найдите вероятность того, что выбранная в магазине сумка окажется с дефектами. Результат округлите до сотых.

Решение:

Событие А = «выбранная в магазине сумка с дефектами», тогда N(A) = 16; N = 154 + 16 = 170.

Ответ: 0,09.

Пример 3

В группе туристов 25 человек. Их вертолетом в несколько приемов забрасывают в труднодоступный район по 5 человек за рейс. Порядок, в котором вертолет перевозит туристов, случаен. Найдите вероятность того, что турист З. полетит вторым рейсом вертолета. Решение:

Так как туристов перевозят по 5 человек за рейс, то во второй группе будет

5 человек. Найдем вероятность того, что один из этих 5-ти – турист З.: N(A) = 5; N = 25.

Ответ: 0,2.

4

В группе туристов 4 человека. С помощью жребия они выбирают двух человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист Д, входящий в состав группы, пойдет в магазин? Решение:

Так как в группе туристов 4 человека, а выбирается 2 человека для похода за продуктами, то достаточно найти вероятность того, что один из этих 2-х – турист Д.:

N(A) = 2; N = 4. =>         

Ответ: 0,5.

Пример 5

Бабушка испекла пирожки с повидлом, капустой и картошкой и выложила их вперемешку на одно блюдо. С повидлом было 8 пирожков, с капустой – 7, а с картошкой – 10. Внешне все пирожки выглядят одинаково. Найдите вероятность того, что случайно взятый внучкой пирожок окажется с капустой.

Решение:

8 + 7 + 10 = 25 – всего пирожков испекла бабушка Событие А = «взятый пирожок с капустой», тогда N(A) = 7; N = 25.

Ответ: 0,28.

Пример 6

Маша, Олег, Соня, Миша и Кирилл играют в классики. Того, кому первым ходить, они определяют жребием. Найдите вероятность того, что начинать будет мальчик. Решение:

В игре участвуют 5 детей, из них 3-е – мальчики (Олег, Миша и Кирилл).

Событие А = «начинать игру будет мальчик», тогда N(A) = 3; N = 5. =>  Ответ: 0,6.      

7

Из множества натуральных чисел от 30 до 41 наудачу выбирают одно число. Какова вероятность того, что оно делится на 5?

Решение:

Множество натуральных чисел от 30 до 41 состоит из 12 чисел.

Чисел из этого множества, делящихся на 5 три (30, 35, 40).

Событие А = «выбранное число делится на 5», тогда N(A) = 3; N = 12.

Ответ: 0,25.

Пример 8

В классе 6 учащихся, среди них два друга – Сергей и Вадим. Класс случайным образом разбивают на две равные группы. Найдите вероятность того, что Сергей и Вадим окажутся в одной группе. Решение:

Пусть один из друзей находится в некоторой группе. Вместе с ним в группе окажутся 2 человека из 5 оставшихся одноклассников.

Событие А = «второй друг окажется среди этих 2 человек». N(A) = 2; N = 5.

Ответ: 0,4.

Пример 9

Коля и Толя играют в кости. Они бросают кубик по одному разу, выигрывает тот, у кого выпадет больше очков. Первым бросил Коля, у него выпало 4 очка. Найдите вероятность того, что Толя не выиграет.

Решение:

Толя не выиграет, если он выбросит 1, 2, 3 или 4 очка.

Событие А = «Толя не выиграет», тогда N(A) = 4; N = 6.

Ответ: 2/3.                                       

10

На фабрике керамической посуды 10% произведенных тарелок имеют дефект. При контроле качества продукции выявляется 55% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Ответ округлите до сотых.

Решение:

Событие А = «выбранная при покупке тарелка не имеет дефектов». Пусть фабрика произвела а тарелок, тогда качественных из них N(A) = 0,9а.

В продажу поступят все качественные тарелки и 100% - 55% = 45% невыявленных дефектных тарелок:

N = 0,9а + 0,45·0,1а = 0,945а тарелок.

Ответ: 0,95.

Пример 11

В классе 12 мальчиков и 13 девочек. 1 сентября случайным образом определяют двух дежурных на 2 сентября, которые должны приготовить класс к занятиям. Найдите вероятность того, что будут дежурить мальчик и девочка. Решение:

Общее число случаев «двое дежурных на 2 сентября» определяется как выбор двух элементов из 25, порядок выбора не важен:

Число случаев «будут дежурить мальчик и девочка» находим по правилу умножения:

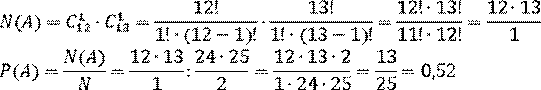
Ответ: 0,52.