Подобие треугольников. Зачет по геометрии 8 класс

Зачет по геометрии         учени___          8       класса __________________________   

Тема: «Подобие треугольников».

1 вариант.

Часть 1.

Определить являются ли ниже приведенные утверждения верными (да, нет)

Часть 2.

Задание 2.  Тест (выберите верный ответ).

№1. Какое из следующих утверждений верно?
1). Два треугольника называются подобными, если углы и стороны одного треугольника пропорциональны углам и сторонам другого.
2). Два треугольника называются подобными, если стороны одного треугольника пропорциональны сторонам другого.
3). Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
4). Два треугольника называются подобными, если стороны одного треугольника равны сторонам другого.

№2. Какое из следующих утверждений верно?
1). Отношение высот двух подобных треугольников равно квадрату коэффициента подобия.                                                                                                                                          2). Отношение высот двух подобных треугольников равно коэффициенту подобия.            

3). Отношение высот двух подобных треугольников равно отношению соответственных углов.                                                                                                                                               

№3. Какое из следующих утверждений верно?
1). Отношение площадей двух подобных треугольников равно коэффициенту подобия.
2). Отношение площадей двух подобных треугольников равно половине коэффициента подобия.
3). Отношение площадей двух подобных треугольников равно половине квадрата коэффициента подобия.
4). Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

Задание 3. 

Решить задачи.

1). Сходственные стороны подобных треугольников ABC и A₁B₁C₁  равны AB = 4,5 см, A₁B_{1 =} 7,5 см_.

а). Найти коэффициент подобия k треугольников ABC и A₁B₁C_1.                                            

б). Найти отношение высот подобных треугольников ABC и A₁B₁C₁ .                                   

в). Найти отношение периметров подобных треугольников ABC и A₁B₁C_1.                           

г). Найти отношение площадей подобных треугольников ABC и A₁B₁C_1.

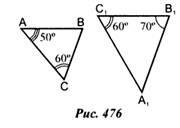
2). Доказать, что треугольники (рис. 476) подобны

Зачет по геометрии          учени __     8       класса ______________________________

 Тема: «Подобие треугольников».

2 вариант.

Часть 1.

Определить являются ли ниже приведенные утверждения верными (да, нет)

Часть 2.

Задание 2.  Тест (выберите верный ответ).

№1. Какое из следующих утверждений верно?                                                                         

1). Коэффициентом подобия называют число k, равное отношению сходственных сторон подобных треугольников.

2). Коэффициентом подобия называют число k, равное отношению соответственных углов подобных треугольников.

3). Коэффициентом подобия называют число k, равное произведению сходственных сторон подобных треугольников.

№2. Какое из следующих утверждений верно?
1). Отношение периметров двух подобных треугольников равно коэффициенту подобия.    

2). Отношение периметров двух подобных треугольников равно квадрату коэффициента подобия.                                                                                                                                          3). Отношение периметров двух подобных треугольников равно половине коэффициента подобия

№3. Какое из следующих утверждений соответствует первому признаку подобия?
1). Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника.
2). Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны.
3). Если два угла одного треугольника соответственно равны двум углам другого треугольника.
4). Если две стороны одного треугольника равны двум сторонам другого треугольника.

Задание 3. 

Решить задачи.

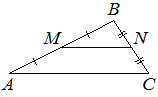
1). По данным рисунка

а). Докажите, что треугольник ABC подобен треугольнику MNB.  

б). Найдите коэффициент подобия треугольников ABC и MNB.

в). Площадь треугольника ABC равна 100 см^2. .  Найдите площадь треугольника MNB.

г). Периметр треугольника MNB равен 39 см^. . Найдите периметр треугольника ABC.

2). Доказать, что треугольники (рис. 477) подобны

Скачано с www.znanio.ru