Лабораторная работа № 3_9. Поиск и принятие решений в

Excel.

Задание 1. Задача об оптимальном ассортименте. Предприятие выпускает 2 вида продукции. Цена единицы 1-го вида продукции - 25 000, 2-го вида продукции – 50000. Для изготовления продукции используются три вида сырья, запасы которого 37, 57,6 и 7 условных единиц. Нормы затрат каждого сырья на единицу продукции представлены в следующей таблице.

Требуется определить плановое количество выпускаемой продукции таким образом, чтобы стоимость произведенной продукции была максимальной

Выполнение.

1.  Такие задачи решаются при помощи инструмента Excel «Поиск решения». Для установки этого инструмента необходимо :

Главное меню: Сервис / Надстройки / Установить флажок «Поиск  решения» / OK.

После загрузки инструмента «Поиск решения» в меню Сервис появляется команда «Поиск решения». Выполнение этой команды начинается с вывода диалогового окна, в котором вводятся исходные данные задачи. 

2.  Математическая модель задачи.

Пусть продукция производится в количестве: 

1-й вид – x₁ единиц, 2-й вид – x₂ единиц.

Тогда стоимость произведенной продукции выражается целевой функцией f(x₁,x₂)=25000 x₁+50000x₂,

для которой необходимо найти максимум.

При этом следует учесть ограничения по запасам сырья: 1,2 x₁+1,9 x₂  37,

2,3 x₁+1,8 x₂  57,6, 0,1 x₁+0,7 x₂  7

и по смыслу задачи  x₁, x₂ должны быть неотрицательными и целыми:  x₁0,  x₂ 0.

3.  Ввод исходных данных в компьютер.

3.1.  Введем целевую функцию и ограничения.

Для переменных x₁,x₂ определим соответственно ячейки С2:D2 и зададим им начальные значения, равные нулю. Затем коэффициенты целевой функции и нормы расхода сырья расположим под неизвестными в ячейках С3:D3 и С6:D8  соответственно. Запасы сырья расположим справа от матрицы норм расхода в ячейках  G6:G8. В ячейке F2 вычислим значение целевой функции, а в ячейках F6:F8 - реальный расход сырья.

3.2.  Задание параметров для диалогового окна «Поиск решения». Выполнить команду Сервис / Поиск  решения.

В диалоговом окне «Поиск  решения» нужно указать:

•     адрес ячейки, в которой находится формула, вычисляющая значение целевой функция;

•     цель вычислений (задать критерий для нахождения экстремального значение целевой функции);

•     адреса ячеек, в которых находятся значения изменяемых переменных х1, х2;

•     матрицу ограничений, для чего нажимается кнопка «Добавить»;

•     параметры решения задачи, для чего нажимается кнопка «Параметры». Диалоговое окно «Поиск решения» и схема расположения исходных данных приведены ниже. Информация в этом окне соответствует решаемой задаче.

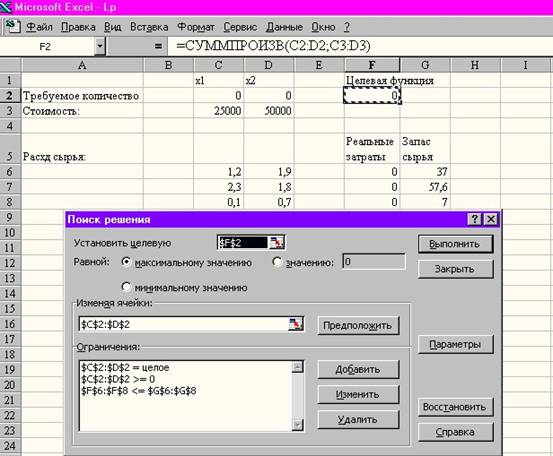
После ввода всех данных и задания параметров нажать кнопку «Выполнить».

Ответ: 825000

2.   Сетевая транспортная задача

Задание 2.1.

Три поставщика одного и того же продукта располагают в планируемый период следующими запасами этого продукта: первый- 120 условных единиц, второй- 100 и третий 80 единиц. Этот продукт должен быть перевезен к трем потребителям, спросы которых соответственно равны 90, 90 и 120 условных единиц. Приведенная ниже таблица содержит показатели затрат, связанных с перевозкой продукта из i-го пункта отправления в j-й пункт потребления.

Требуется перевезти продукт с минимальными затратами.

Математическая модель задачи выглядит следующим образом.

Целевая функция имеет вид:

F(x)=7 x₁₁+6 x₁₂+4 x₁₃+3 x₂₁+8 x₂₂+5 x₂₃+2 x₃₁+3 x₃₂+7 x_33 min,

Ограничения имеют вид: x₁₁+x₁₂+x₁₃=120,   x₂₁+x₂₂+x₂₃=100,   x₃₁+x₃₂+x₃₃=80,     x₁₁+x₂₁+x₃₁=90, x12+x22+x32=90,  x13+x23+x33=120, x_ij 0, i, j=.

Искомые значения xij находятся в блоке ячеек B4:D6. Адрес данного блока входит в поле ввода Изменяя ячейки в окне “Поиск решения” . Требования к ограничениям по спросу и запасам представлены соответственно в ячейках B7:D7 и E4:E6. Коэффициенты ЦФ, означающие затраты на доставку расположены в блоке ячеек B12:D14.

Формулы целевой функции и ограничений находятся соответственно в ячейке F8 и ячейках B8:D8 (ограничения по спросу), F4:F6 (ограничения по запасам) . Вид электронной таблицы в режиме отображения формул представлен на рис. 

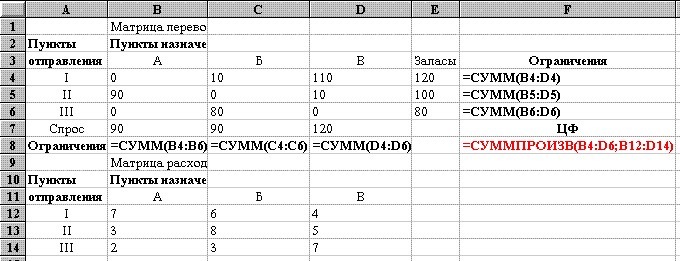
Первая запись в группе Ограничения  представляет ограничения по нижней границе xij. Вторая и третья записи выражают ограничения по уровню спроса и запасов соответственно.

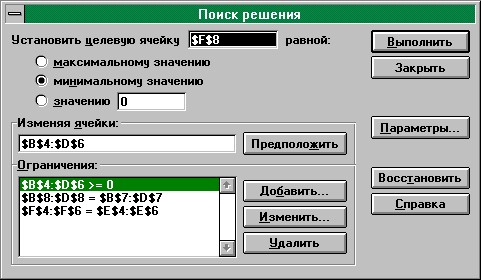
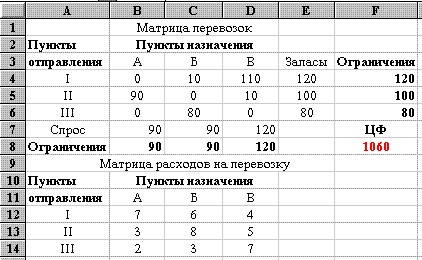
Окончательный вид электронной таблицы Excel, созданной для решения задачи. 

Задание 2.2.

На складах имеется груз, количество которого определяется в следующей таблице:

Этот груз необходимо перевезти в пункты назначения в соответствии с таблицей:

Стоимость перевозок определяется таблицей:

Необходимо составить план перевозок так, чтобы стоимость перевозок была минимальной.

Ответ: 1286.

Задание 3. Задача о смесях. Фирма «Корма»  имеет возможность  покупать 4 различных вида зерна (компонентов смеси) и изготавливать различные виды кормов. Разные зерновые культуры содержат разное количество питательных ингредиентов. Произведенный комбикорм должен удовлетворять некоторым минимальным  требованиям с точки зрения питательности. Требуется определить, какая из возможных смесей является  самой дешевой. Исходные данные приведены в следующей таблице

Ответ: 21778.

Задание 4. Балансовые модели. Имеется трехотраслевая балансовая модель экономики с  матрицей a_i,j коэффициентов затрат:

0,1   0,05   0,2 

                                                                                                 

0,3   0        0,15

                                                                       ^0,2   0,4     0 ^_

Производственные мощности отраслей ограничивают возможности ее валового выпуска числами M_i = {300, 200. 500}. Определить оптимальный валовой выпуск всех отраслей X_i, максимизирующий  стоимость суммарного конечного продукта Y_i, если задан вектор цен C_i на конечный продукт (2, 5, 1). Конечный продукт определяется формулой 

3

Y_i  = X_i  - (a_{i, j} X _j)   i=1,2,3

j1

3

Целевая функция F(x₁,x₂,x₃) ⁼ y_i c_i  max

i1

Ограничения валового выпуска xi _ mi

Ответ: 909

Задание 4а. Решить эту же задачу, если накладываются следующие ограничения на валовой выпуск продукции и конечный продукт отраслей:

валовый выпуск : X₁ : X₃ = 2 : 1  , конечный продукт: Y₂  <=100

Ответ: 907,5

Задание 4б. К данным задачи 4 заданы коэффициенты прямых затрат труда на выпуск продукции каждой отрасли. Определить максимально возможный выпуск конечного продукта в стоимостном выражении, если суммарные затраты труда не должны превышать заданного числа единиц.

Ответ: 789