Поляризованный свет. Эллипс поляризации.

1.1.     Поляризованный свет. Эллипс поляризации.

Свет, обладающий преимущественным направлением колебаний (вращения) электрического и, соответственно, магнитного векторов называется поляризованным. Поляризованный свет принято изображать в виде проекции колебания конца электрического вектора на плоскость перпендикулярную направлению распространения света, для наблюдателя, смотрящего навстречу распространяющейся волне. Изображение направления вращения электрического вектора, а также отсчёт угла его поворота производится по правилу правого винта [183].

При рассмотрении отражения луча поляризованного света от некой поверхности (исследуемого образца) удобно пользоваться системой координат одна из осей которой, параллельна плоскости образца s, а другая – параллельна плоскости падения луча света на образец p (плоскость, в которой лежат падающий и отраженный лучи, а также нормаль к поверхности образца).

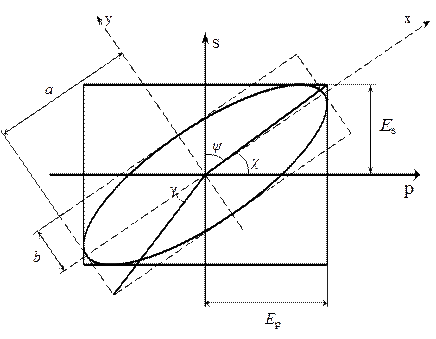
В общем случае поляризованный свет обладает эллиптической поляризацией и его можно представить в виде суперпозиции лучей, поляризованных линейно в направлениях p и s. Характеристиками эллипса поляризации являются азимут восстановленной линейной поляризации , разность фаз p- и s-составляющих колебаний , азимут большего диаметра  и эллиптичность  (Рис. 2.1). Связь между этими параметрами определяется выражениями [7]:

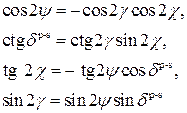                                                                                        (2.1)

Из четырёх параметров эллипса поляризации в качестве независимых могут быть выбраны любые два, однако общепринятым является использование величин  и .

1.2.     Отражение и преломление электромагнитных волн в многослойных проводящих структурах.

Процессы преломления и отражения на границе j-того и j+1-го слоёв многослойной структуры (Рис. 2.2) удобно описывать с помощью линейного оператора

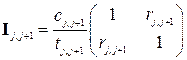                                           .                                           (2.2)

Для s-поляризации: ,  – амплитудные коэффициенты Френеля отражения и пропускания, . Для p-поляризации: , , .

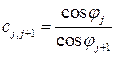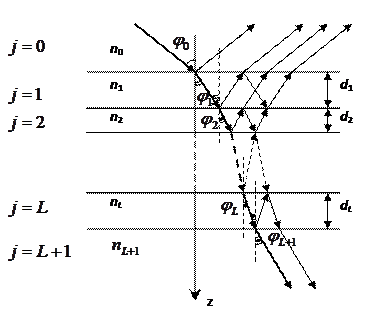
Рис. 2.2 Отражение и пропускание света при наклонном падении системой L плоско-папраллельных слоёв. (Не все многократные отражения показаны).

Оператор  связывает между собой комплексные амплитуды напряженностей электрического поля  в каждом из слоёв:

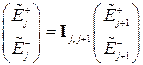                                                .                                                (2.3)

Здесь верхний индекс «+» соответствует волне распространяющейся в направлении оси z, а «-» – распространяющейся в противоположном. Аналогично можно записать и преобразование, описывающее набег фазы в j-том слое:

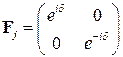                                                  ,                                                  (2.4)

где ,  – показатель преломления слоя,  – толщина слоя,  – угол между волновым вектором и нормалью к границе раздела,  – длинна волны зондирующего излучения. Матрица (2.4) называется фазовой или интерференционной.

Таким образом, прохождение электромагнитной волны через многослойное покрытие разделяющее (L+1)-вую и 0-вую среды, и состоящее из  прозрачных изотропных диэлектриков разделённых плоскопараллельными границами (рис. 1.2) описывается матрицей

                                      .                                      (2.5)

Матрица  называется матрицей рассеяния. Она позволяет вычислить обобщённые коэффициенты отражения и пропускания рассматриваемой системы:

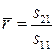                                                        ,                                                        (2.6)

                                                        ,                                                         (2.7)

соответственно. Здесь  и  – компоненты матрицы  [184].

Для удобства описания распространения электромагнитных волн в проводящих средах используется комплексная диэлектрическая проницаемость [7]

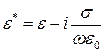                                                   ,                                                    (2.8)

и комплексный показатель преломления проводящей среды:

                                                 .                                                 (2.9)

Из комплексности показателя преломления проводящей среды следует комплексность угла преломления. Это позволяет формально пользоваться законом Снеллиуса и формулами Френеля того же вида, что и для диэлектриков. Матрици преломления, набега и рассеяния имеют тот же вид, но содержат комплексные амплитудные коэффициенты отражения и пропускания.

1.3.     Расчёт оптического пропускания.

Измерения коэффициента оптического пропускания обычно производятся при нормальном падении света на образец. В этом случае различие между Френелевскими коэффициентами для p- и s-поляризации исчезает, и они принимают вид:

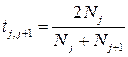                                                 ,                                               (2.10)

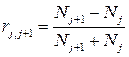                                                 .                                               (2.11)

Поскольку тонкоплёночные покрытия обычно наносят на подложки, толщина которых , а используемый в спектрофотометрах свет не является строго монохроматичным, интерференция от подложки не наблюдается. Для учёта этого обстоятельства, после нахождения обобщённого энергетического коэффициента пропускания согласно выражению

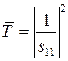                                                                                                              (2.12)

производится усреднение по набегу фазы в подложке  в интервале от 0 до π [185].

Таким образом, для чистой непоглощающей подложки:

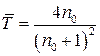                                                    .                                                  (2.13)

Для однослойной модели поглощающей плёнки на прозрачной подложке также возможно использовать приближённую формулу вида:

                                                      ,                                                    (2.14)

полученную в предположении о малости коэффициентов отражения на границах. Здесь , а .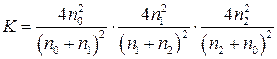

Однако в общем случае корректным способом учёта степени монохроматичности света при расчёте оптического пропускания будет численное усреднение величины  по интервалу .

1.4.     Связь показателя преломления с химическим составом и структурой вещества.

Известно, что приложение внешнего электрического поля к диэлектрику приводит к поляризации последнего. В области оптических частот, из всего множества механизмов возникновения поляризации действует только упруго-электронный. Упруго-электронная поляризация диэлектриков обусловлена смещением электронных оболочек атомов под действием электрического поля. Электронная поляризуемость, различных атомов различна и в классическом приближении пропорциональна объёму атома V [186]:

                                                        ,                                                      (2.15)

Электронная поляризуемость единицы массы вещества в высокочастотном поле световой волны характеризуется удельной рефракцией , которая, в отсутствие дисперсии, связана с показателем преломления формулой Лоренца-Лорентца [187]:

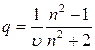                                                    .                                                   (2.16)

Где  – плотность вещества.

Однако удельная рефракция не отражает свойств соединений, состоящих из различного числа одинаковых структурных единиц. Поэтому для описания преломляющих свойств химических соединений используется характеристика, называемая молекулярной рефракцией:

                                                      ,                                                    (2.17)

где  – число Авогадро. Молекулярная рефракция является электронной (атомной) поляризуемостью 1 моль вещества.

Таким образом, выражение (2.16) можно представить в виде:

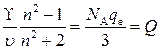                                              ,                                            (2.18)

где  – молярная масса.

Молекулярная рефракция непосредственно связана с составом химического соединения. В основе молекулярной рефрактометрии лежат принципы аддитивности и геометрия расположения атомов в соединении: молекулярная рефракция химического соединения равна сумме рефракций отдельных элементов с учетом характера их связи и координации в соединении. Последнее особенно важно для кристаллических твёрдых тел.

В настоящее время разработаны системы атомных, ковалентных, ковалентных кристаллических и ионных рефракций элементов [186], основанные на расчетах и многочисленных экспериментальных данных. При этом под атомными рефракциями понимаются рефракции изолированных атомов, под ковалентными – рефракции ковалентно связанных атомов, под кристаллическими ковалентными – рефракции атомов с учетом характерных координаций. Система ионных рефракций учитывает размеры ионов в зависимости от их валентности (заряда иона).

Скачано с www.znanio.ru