Поделиться
4. Понятие о системе счисления. Двоичная система счисления.doc
Понятие о системе счисления. Двоичная система счисления
Цели урока:
• формирование представлений о позиционных и непозиционных системах счисления;
• формирование знаний о двоичной системе счисления;
• развитие познавательного интереса, логического и алгоритмического мышления, самооценки, навыков самоконтроля.
Тип урока: урок усвоения новых знаний.
Учащиеся должны знать: понятия «позиционная система счисления» и «непозиционная система счисления», назначение двоичной системы счисления.
Учащиеся должны уметь: приводить примеры использования позиционной и непозиционной систем счисления; с помощью стандартного приложения Калькулятор переводить целые числа из десятичной системы счисления в двоичную и обратно.
Ход урока:
1. Организационный момент;
2. Проверка полученных знаний;
|
Кодирование информации. Единицы измерения объема информации |
|
|
Вариант 1 1. Что такое кодирование? 2. Что такое бит? 3. Какое представление называют двоичным? 4. Что такое система счисления? 5. Что такое позиционная система счисления? |
Вариант 2 1. Что такое декодирование? 2. Чему равен 1 байт? 3. Какой код называют двоичным? 4. Что такое непозиционная система счисления? 5. Что такое разряд числа? |
|
Кодирование – это процесс преобразования информации из одной формы представления в другую, более удобную для хранения, передачи или обработки. Обратный процесс называется декодированием. Бит – это самая маленькая единица информации, которая может иметь два состояния. Последовательность из восьми бит образует 1 байт. Для цифрового представления информации в компьютере используется только две цифры: 0 и 1. Такое представление называют двоичным. Набор из нулей и единиц называют двоичным кодом или двоичным числом. Система счисления – способ записи чисел с помощью заданного набора специальных знаков (цифр). В позиционной системе счисления значение каждой цифры в числе зависит от ее позиции в числе. Примером позиционной системы счисления является десятичная система счисления. В непозиционной системе счисления значение цифры в числе не зависит от ее позиции в числе. Примером непозиционной системы счисления является римская система счисления. Основанием системы счисления является количество цифр, которые используются при записи чисел. Позицию цифры в числе называют разрядом. |
|
3. Объяснение нового материала;
Правило перевода десятичного числа в двоичную систему счисления
Чтобы перевести целое десятичное число в двоичную систему счисления, надо это число разделить на 2. Если полученное частное больше 1, то его основание снова необходимо разделить на 2 и т.д., пока частное не станет равным 1. В результате нужно записать в одну строку последнее частное и все остатки, начиная с последнего.
Правило перевода из двоичной системы счисления в десятичную систему счисления
Чтобы перевести число из двоичное систему счисления в десятичную, надо двоичное число представить в виде суммы степеней двойки с коэффициентами-цифрами и найти сумму
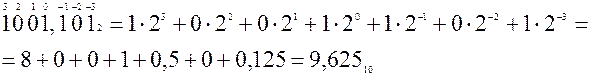
4. Выполнение практических заданий;
Задание 1. Переведите числа из десятичной системы счисления в двоичную.
а) 6110=
б) 8710=
в) 201010=
г) 6410=
д) 10510=
Задание 2. Переведите двоичные числа в десятичную систему счисления
а) 11012=
б) 110001,112=
в) 10010012=
г) 100111,12=
д) 110,1012=
5. Домашнее задание: §3
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
