


Изучая поведение функции y=f(x) около конкретной точки х0, важно знать, как
меняется значение функции при изменении значения аргумента. Для этого используют понятия приращения аргумента и функции.
Рассмотрим функцию y = f(x)
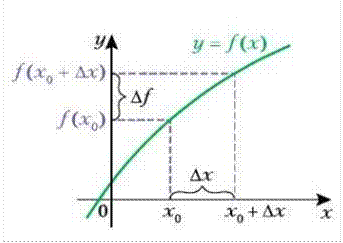
Выберем произвольную фиксированную точку х0. Дадим точке х0 некоторое приращение ∆х, т. е. сместим точку х0 на некоторое расстояние ∆х.
∆х=х−х0 – называется приращением аргумента
∆𝑦 =𝑓![]() 𝑥0+∆𝑥
𝑥0+∆𝑥![]() −𝑓(𝑥0)- называется приращением
функции
−𝑓(𝑥0)- называется приращением
функции
Если ∆х → 0, то точка х будет приближаться к точке х0 и f(x) будет приближаться к f(x0).
Отношение приращения функции к приращению
аргумента т. е. ![]() ∆𝑦
показывает, сколько единиц
∆𝑦
показывает, сколько единиц
∆𝑥
приращения функции приходится на единицу приращения аргумента и называется средней скоростью изменения функции y для промежутка значений аргумента от х0 до 𝑥0 + ∆𝑥
![]() ∆
∆![]() 𝑦
=
𝑓 𝑥0+∆𝑥 −𝑓(𝑥0)
-средняя скорость изменения функции
𝑦
=
𝑓 𝑥0+∆𝑥 −𝑓(𝑥0)
-средняя скорость изменения функции
∆𝑥 ∆𝑥
y для промежутка значений аргумента от х0 до 𝑥0 + ∆𝑥
При ∆х → 0 мы получим предел отношения приращения функции к приращению аргумента, т.е.
∆𝑦
lim ![]() –
называется мгновенной (истинной)
–
называется мгновенной (истинной)
∆𝑥→0∆𝑥
скоростью изменения функции при данном значении аргумента.
![]() lim
lim ![]() ∆𝑦
=
lim 𝑓
𝑥0+∆𝑥 −𝑓(𝑥0) = 𝑓∕(𝑥)-
производная
∆𝑦
=
lim 𝑓
𝑥0+∆𝑥 −𝑓(𝑥0) = 𝑓∕(𝑥)-
производная
∆𝑥→0∆𝑥 ∆𝑥→0 ∆𝑥 функции
Определение Производной функции y=f(x) называется предел отношения приращения функции к приращению аргумента при ∆х → 𝟎.
Операция нахождения производной функции называется дифференцированием.
Если функция y=f(x) имеет производную в точке х, то ее называют дифференцируемой в точке х.
Если функция дифференцируема в точке х, то она и непрерывна в этой точке.
Алгоритм нахождения производной (для функции
y=f(x))
1. Зафиксировать значение х0, найти f(х0).
2.
Дать
аргументу х0 приращение ∆х,
перейти в новую точку х0+∆х,
найти 𝑓![]() 𝑥0
+ ∆𝑥
𝑥0
+ ∆𝑥![]()
3.
Найти
приращение функции: ∆𝑦 = 𝑓![]() 𝑥0
+ ∆𝑥
𝑥0
+ ∆𝑥![]() − 𝑓(𝑥0)
− 𝑓(𝑥0)
4.
Составить
отношение ![]() ∆𝑦
∆𝑦
∆𝑥
5.
Вычислить
lim
![]() ∆𝑦
∆𝑦
∆𝑥→0 ∆𝑥
6. Этот предел и есть 𝑓∕(𝑥)
Пример 1: Найти производную функции y = x2 в точке х0
Решение:
1)Фиксируем значение аргумента х = х0 и находим значение функции 𝑓(𝑥0) т.е. f(x0) = (x0)2
2) Задаем аргументу приращение ∆𝑥 т.е.
х = 𝑥0 +
∆𝑥 и находим значение функции 𝑓![]() 𝑥0
+ ∆𝑥
𝑥0
+ ∆𝑥![]() , т.е.
, т.е.
𝑓![]() 𝑥0 +
∆𝑥
𝑥0 +
∆𝑥![]() = ( х0 + ∆𝑥)2=
(х0)2+2х0∆х + ∆х2
= ( х0 + ∆𝑥)2=
(х0)2+2х0∆х + ∆х2
3)Находим приращение функции ∆𝑓
= 𝑓![]() 𝑥0 + ∆𝑥
𝑥0 + ∆𝑥![]() − 𝑓(𝑥0)
− 𝑓(𝑥0)
Т.е. ∆𝑓 = (х0)2+2х0∆х + ∆х2 −(x0)2 = 2х0∆х + ∆х2
Пример
1: Найти производную функции y = x2 в
точке х0 4)Находим отношение ![]() .
.
∆𝑥
∆𝑓 2х0∆х + ∆х2 ∆𝑥(2х0 + ∆𝑥)
 𝑥
𝑥
5)Находим предел ![]() .
.
∆𝑥→0∆𝑥
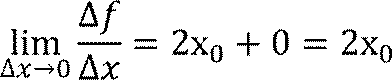
6)Таким образом 𝑓∕(𝑥) = 2х
![]() Пример2:
Вычислить значение производной функции f(x)= 3𝑥+1 в
точке х0 Решение:
Пример2:
Вычислить значение производной функции f(x)= 3𝑥+1 в
точке х0 Решение:
![]() 1)Фиксируем
значение аргумента х = х0 и находим значение функции 𝑓(𝑥0)
т.е. f(x0) = 3𝑥0 + 1 2)Задаем
аргументу приращение ∆𝑥
т.е.
1)Фиксируем
значение аргумента х = х0 и находим значение функции 𝑓(𝑥0)
т.е. f(x0) = 3𝑥0 + 1 2)Задаем
аргументу приращение ∆𝑥
т.е.
х = 𝑥0 +
∆𝑥 и находим значение функции 𝑓
𝑥0 + ∆𝑥![]() , т.е.
, т.е.
𝑓![]() 𝑥0
+ ∆𝑥
𝑥0
+ ∆𝑥![]() = 3 𝑥0 +
∆𝑥 + 1
= 3 𝑥0 +
∆𝑥 + 1
 3)Находим
приращение функции ∆𝑓 = 𝑓 𝑥0 +
∆𝑥
3)Находим
приращение функции ∆𝑓 = 𝑓 𝑥0 +
∆𝑥![]() − 𝑓(𝑥0)
− 𝑓(𝑥0)
![]() т.е. ∆𝑓
= 3 𝑥0 + ∆𝑥 + 1 − 3𝑥0
+ 1
т.е. ∆𝑓
= 3 𝑥0 + ∆𝑥 + 1 − 3𝑥0
+ 1
![]() Пример2:
Вычислить значение производной функции f(x)= 3𝑥+1 в
точке х0
Пример2:
Вычислить значение производной функции f(x)= 3𝑥+1 в
точке х0
![]() 4)Находим отношение
4)Находим отношение ![]() ∆𝑓
т.
∆𝑓
т.![]() 3 𝑥0+∆𝑥
+1− 3𝑥0+1
3 𝑥0+∆𝑥
+1− 3𝑥0+1
∆𝑥 ∆𝑥 ∆𝑥
5)Находим предел ![]() т.е.
т.е.
∆𝑥→0 ∆𝑥
![]()
![]() ∆𝑓 3
𝑥0 + ∆𝑥 + 1 − 3𝑥0 +
1
∆𝑓 3
𝑥0 + ∆𝑥 + 1 − 3𝑥0 +
1
 lim =
lim
lim =
lim
∆𝑥→0 ∆𝑥 ∆𝑥→0 ∆
6)Таким образом 𝑓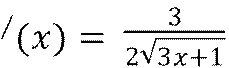
Вычислите производные следующих функций:
1. F(x) = 2x+3 в точке х=3;
2. F(x)=3х2-2 в точке х=0;
3. F(x)=5x-x2 в точке х=1;
4.
F(x)=![]() 1
в точке х= -1;
1
в точке х= -1;
𝑥+3
5.
F(x)=
sin x в точке х= ![]() 𝜋 ;
𝜋 ;
4 6.
F(x)= cos x в точке х=− ![]() 𝜋;
3
𝜋;
3
7.
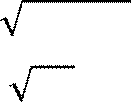 F(x)=
2𝑥
− 5 в точке х=2;
F(x)=
2𝑥
− 5 в точке х=2;
8. F(x)= 3𝑥+5 в точке х=5
Таблица производных
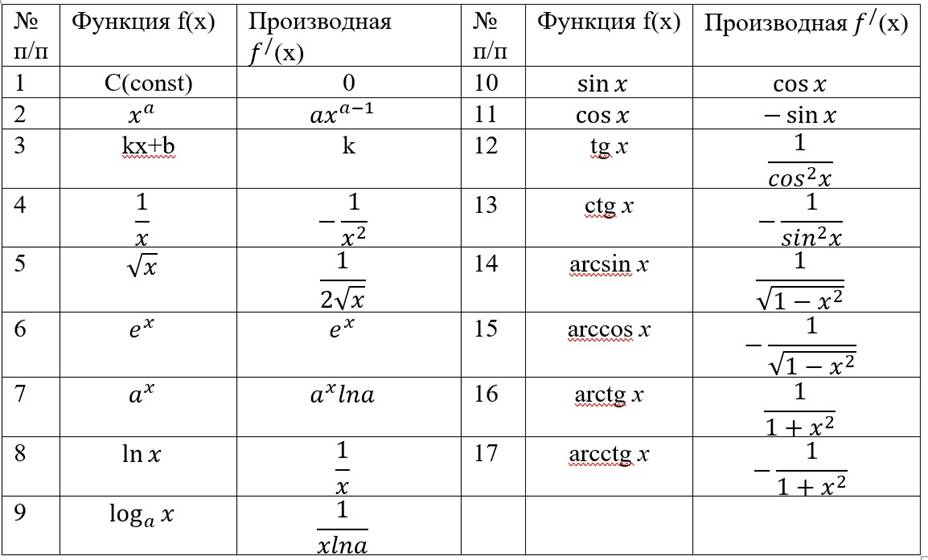
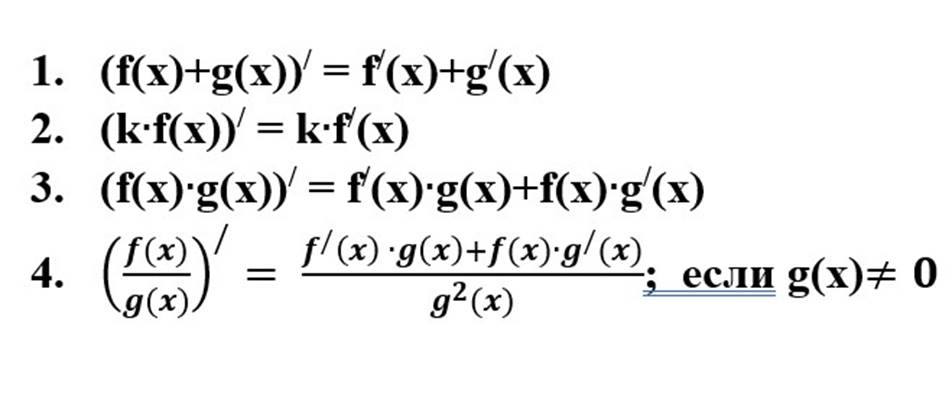 |

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.