ПОНЯТИЕ РЕШЕНИЯ СИСТЕМЫ НЕРАВЕНСТВ

Понятие решения системы неравенств
с одной переменной

Цели: ввести понятия системы неравенств с одной переменной, решения системы неравенств; формировать умение решать системы неравенств с помощью геометрической модели числовых промежутков.

Ход урока

I. Организационный момент.

II. Проверочная работа.

В а р и а н т  1

1. Решить неравенство:

а) 2х – 1 ≤ 2(х – 1);                   б) 3х < 7.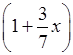

2. При каких значениях х функция у = 0,5х – 11 принимает отрицательные значения?

В а р и а н т  2

1. Решить неравенство:

а) 3(х + 1) ≥ 3х + 1;                   б) 8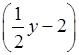 > 4у.

2. При каких значениях х функция у = 1,5х – 9 принимает положительные значения?

О т в е т ы:

III. Актуализация знаний.

1. Изобразите на координатной прямой и запишите, используя введенные обозначения, промежуток, задаваемый условием:

а) х > 1,5;           б) х ≤ 3,2;           в) 0 < х ≤ 1;           г) –5 ≤ х ≤ –3.

2. Используя координатную прямую, найдите пересечение промежутков:

а) (–∞; 6] и (3; +∞);                               в) (–3; 0] и (0; +∞);

б) (–∞; 2) и [4; +∞);                              г) (–∞; 0] и (–∞; 4).

IV. Объяснение нового материала.

Объяснение материала проводится в  т р и   э т а п а.

На первом этапе рассматривается задача, решение которой приводит к понятию «система неравенств с одной переменной» и «решение системы неравенств с одной переменной». На втором этапе рассматривается способ решения системы неравенств. На третьем этапе приводятся различные примеры решения систем неравенств.

1-й  э т а п.

Рассматриваем задачу со с. 184 учебника.

Анализ текстовой задачи показывает две основных зависимости, которые могут быть записаны в форме неравенств. Требуется найти значения переменной, удовлетворяющие одновременно обоим неравенствам.

Теперь появляется возможность ввести новое понятие. Сообщаем учащимся, что в тех случаях, когда нужно найти общее решение двух и более неравенств, говорят, что требуется решить систему неравенств. Затем вводим определение:

Решить систему – значит найти все её решения или доказать, что решений нет.

2-й  э т а п.

Теперь перед учащимися возникает новая проблема: как решить полученную систему неравенств. Мы умеем решать отдельно неравенство, тогда получим:

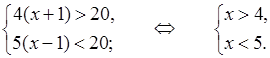
Получили, что множество решений первого неравенства есть открытый числовой луч (4; +∞), а второго – (–∞; 5). Пересечение этих двух числовых промежутков и будет являться решением системы неравенств:

           (–∞; 5) (4; +∞) = (4; 5).

Решение можно записать как в виде числового промежутка, так и соответствующего ему неравенства: 4 < x < 5.

3-й  э т а п.

Рассмотрим примеры 1–4 на с. 185–187 учебника. Это поможет увидеть различные варианты получаемых решений: интервалы, числовые лучи, пустое множество.

Таким образом, учащиеся наметили несложный алгоритм решения системы неравенств с одной переменной:

1-й  ш а г. Решаем каждое неравенство системы отдельно.

2-й  ш а г. Находим пересечение числовых промежутков, являющихся решением неравенств системы, с помощью координатной прямой.

3-й  ш а г. Записываем полученное решение в виде числового промежутка или неравенства.

V. Формирование умений и навыков.

На уроке учащиеся должны выполнить задания двух групп.

В  п е р в у ю   г р у п п у  входят задания на отработку новых терминов и символики, а также на геометрическую интерпретацию решения систем неравенств. Во  в т о р о й   г р у п п е  будут задания на решение несложных систем неравенств.

1. № 874, № 875 – устно.

2. № 876.

Р е ш е н и е

а) 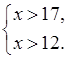        ;      (17; +∞); x > 17.

б) 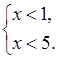 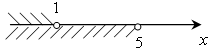          ;     (–∞; 1); х < 1.

в) 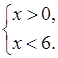           ;       (0; 6); 0 < x < 6.

г) 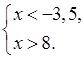     ;         ; нет решений.

д) 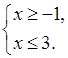        ;         [–1; 3]; –1 ≤ х ≤ 3.

е) 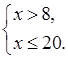        ;        (8; 20]; 8 < x ≤ 20.

О т в е т: а) (17; +∞); б) (–∞; 1); в) (0; 6); г) нет решений; д) [–1; 3]; е) (8; 20].

№ 877 (б, г).

Р е ш е н и е

б)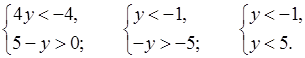

            (–∞; –1); у < –1.

г)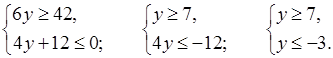

            ; нет решений.

О т в е т: б) (–∞; –1); г) нет решений.

№ 879 (б, г).

Р е ш е н и е

б)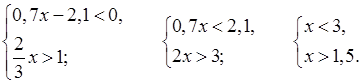

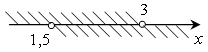            (1,5; 3).

г)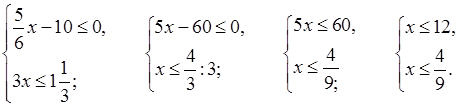

            .

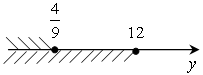
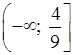О т в е т: б) (1,5; 3); г) .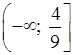

VI. Итоги урока.

В о п р о с ы   у ч а щ и м с я:

– Что называется решением системы неравенств?

– Является ли решением системы неравенств 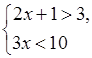 число 3? число 5?

– Что значит «решить систему неравенств»?

Домашнее задание: № 877 (а, в), № 878, № 879 (а, в), № 880.