УДК 372.8:51                                                                                                          16+

ББК 74.262.21

             М34

Серия «Школа России» основана в 2001 году

Авторы: С. И. Волкова, С. В. Степанова, М. А. Бантова, Г. В. Бельтюкова

Математика. Методические рекомендации. 2 класс  :

М34 учеб. пособие для общеобразоват. организаций  /  С. И. Волкова, С. В. Степанова, М. А. Бантова, Г. В. Бельтюкова. — 3-е изд., дораб. — М. : Просвещение, 2017. — 154 с. — (Школа России). — ISBN 978-5-09-051718-8.

Данное пособие призвано способствовать реализации в практике учителя требований к результатам освоения основной образовательной программы начального общего образования, определённых ФГОС. В пособии представлены научно-методические основы курса и их реализация в УМК для 2 класса, тематическое планирование, планируемые результаты (личностные, метапредметные и предметные) по итогам обучения во 2 классе, примеры разработок уроков.

УДК 372.8:51

ББК  74.262.21

ISBN 978-5-09-051718-8 © Издательство «Просвещение», 2017  © Художественное оформление.

                                                                                  Издательство «Просвещение», 2017

                                                                              Все права защищены

ВВЕДЕНИЕ

Настоящее пособие посвящено методике обучения математике во 2 классе и составлено в соответствии с «Рабочей программой по математике»^[1], разработанной на основе Федерального государственного образовательного стандарта начального общего образования (ФГОС НОО) и учебника «Математика» для 2 класса^[2], который входит в завершённую предметную линию учебников «Математика» авторского коллектива М. И. Моро и др. для начальных классов общеобразовательной школы.

В пособии излагаются концептуальные основы курса математики, отражены те изменения в содержании и структуре учебника «Математика. 2 класс», которые были внесены в него в связи с новыми требованиями к обучению в современной начальной школе и изложены в текстах ФГОС НОО второго поколения. В пособии описаны особенности методики работы при изучении математики во 2 классе, ориентированные на достижение личностных, метапредметных и предметных результатов.

На страницах пособия учитель найдёт раздел «Планируемые результаты (предметные, личностные, метапредметные) по итогам обучения во 2 классе», где перечислены универсальные учебные действия (УУД), которые формируются у учащихся в процессе обучения математике во 2 классе, а также те предметные результаты обучения, которые должны быть достигнуты учащимися к концу 2 класса.

В помощь учителю в конце настоящего пособия даётся примерное распределение материала учебника по четвертям учебного года и по урокам.

Предложенное планирование носит приблизительный характер. Естественно, что обучение строится с учётом особенностей класса и условий работы с ним, а это влечёт за собой возможные (по усмотрению учителя) изменения в планировании.

НАУЧНО-МЕТОДИЧЕСКИЕ ОСНОВЫ КУРСА МАТЕМАТИКИ И ИХ РЕАЛИЗАЦИЯ В УМК ДЛЯ 2 КЛАССА

Предлагаемый курс математики, реализованный в завершённой предметной линии учебников «Математика» (авторы М. И. Моро и др.), разработан в соответствии с возрастными особенностями младших школьников, психолого-дидактическими закономерностями формирования знаний, с учётом специфики учебного предмета «Математика». Курс позволяет органически сочетать в образовательном процессе обучение, умственное развитие и воспитание ребёнка, с учётом современных достижений в области информационно-коммуникационных технологий на уровне образовательной программы по математике (ступени обучения) и с учётом тех требований, которые выдвигает к образованию общество на современном этапе его развития и которые отражены во ФГОС НОО.

Основными целями математического образования в начальной школе являются:

•         обеспечение интеллектуального развития ребёнка (математических знаний, мышления, пространственного воображения, речи);

•         формирование универсальных учебных действий на основе математического содержания курса;

•         обеспечение осознания школьниками универсальности математических способов познания закономерностей окружающего мира (взаимосвязей и зависимостей между объектами, процессами и явлениями действительности) и формирование умений использовать (читать и строить) наглядные модели, отражающие количественные и пространственные отношения между объектами;

•         формирование и развитие интереса к умственному труду, творческих возможностей, мотивации к обучению, умений применять полученные знания для получения новых знаний, умения учиться.

Для достижения поставленных целей необходимо решение следующих задач:

•         формирование элементов самостоятельной интеллектуальной деятельности на основе овладения несложными математическими методами познания окружающего мира (умения устанавливать, описывать, моделировать и объяснять количественные и пространственные отношения между объектами);

•         формирование системы начальных математических знаний и умений их применять для решения учебно-познавательных и практических задач;

•         развитие основ логического, знаково-символического, алгоритмического мышления, пространственного воображения и речи младших школьников;

•         формирование универсальных учебных действий, позволяющих учащимся ориентироваться в различных предметных областях знаний и усиливающих мотивацию к обучению; вести поиск информации, фиксировать её разными способами и работать с ней; развивать коммуникативные способности, формирование критичности мышления, умения аргументированно обосновывать и отстаивать свои суждения, оценивать и принимать суждения других; осваивать навыки самоконтроля и самооценки;

•         развитие творческих способностей.

Содержание учебника обеспечивает успешное решение перечисленных задач.

За основу построения данного курса взята авторская концепция наиболее полного использования специфики учебного предмета «Математика» для интеллектуального развития личности. Имеются в виду большие возможности этого учебного предмета как в сфере формирования особого способа мышления детей (развития логического, алгоритмического мышления и пространственного воображения), так и в области освоения ими универсального языка описания многочисленных объектов, явлений и процессов окружающего мира, включая знаково-символический язык математики и способ моделирования.

Содержание учебников строится на основе универсальности математических способов познания закономерностей окружающего мира, позволяющей начать формировать у учащихся целостное восприятие мира и выстраивать модели его отдельных процессов и явлений. Учебник ориентирован на овладение универсальными учебными действиями (личностными, регулятивными, познавательными и коммуникативными) и предметными результатами, обеспечивающими интеллектуальное развитие ребёнка, которое включает в себя накопленные знания по предмету и развитую способность к самостоятельному поиску и усвоению новых знаний, новых способов действий, что составляет основу умения учиться.

Основным в учебнике продолжает оставаться арифметический материал. Поскольку за первый год обучения дети уже познакомились с числами от 1 до 20, их названиями, последова тельностью, составом из двух чисел (для чисел от 11 до 20 — из десятка и единиц) и даже с табличным сложением однозначн ых чисел и соответствующими случаями вычитания (с переходом через десяток), они оказались подготовленными к расшире нию области изучаемых чисел до 100, чему и посвящён рассматриваемый учебник.

Основными вопросами программы второго года обучения являются отработка табличного сложения и вычитания, устное и письменное сложение и вычитание в пределах 100 и в конце го да — ознакомление с умножением и делением.

Важная задача при изучении чисел от 1 до 100 — отработка табличного сложения и вычитания. Продолжается практическое использование связи между сложением и вычитанием, что даёт возможность опираться на знание состава чисел и результа тов сложения при нахождении разности в соответствующих слу чаях вычитания.

Чтобы обеспечить прочное, доведённое до автоматизма усвоение таблицы сложения, важно продолжить систематическую тренировочную работу и обеспечить непрерывный контроль за усвоением знаний каждым из учеников.

Продолжая давать ученикам установку на запоминание табли цы, во 2 классе, следуя за учебником, учитель повторяет с детьми общие приёмы сложения и вычитания с переходом через десяток, стремясь к сокращению рассуждений всех учащихся и поощряя воспроизведение результата по памяти. В случае неверного ответа следует потребовать от ученика развёрнутое пояснение хода вычислений.

Знание наизусть результатов сложения и вычитания с пере ходом через десяток совершенствуется на протяжении всего периода изучения устного сложения и вычитания в предел ах 100, и к моменту перехода к работе над письменными выч ислениями во 2 классе все дети должны знать табличные слу чаи сложения и вычитания наизусть.

Безусловно, знание результатов сложения и вычитания с пер еходом через десяток будет совершенствоваться при изучении письменного сложения и вычитания в пределах 100, и в отличие от 1 класса оно уже входит в основные требования к знаниям учащихся к концу второго года обучения.

Нумерация чисел в пределах 100, а также внетабличное сло жение и вычитание составляют основное содержание программы 2 класса.

Устные приёмы сложения и вычитания в пределах 100 изучаю тся в последовательности и системе, представленной в учебнике. Она в основном хорошо знакома учителю и оправдала себя в практике обучения. Все устные приёмы сложения в пределах 100 рассматриваются с опорой на одно простейшее правило: «Единицы складывают с единицами, десятки — с десятками». Что же касается практического ознакомления с сочетательным свойством сложения, следует обратить внимание, что оно являе тся не теоретической основой при рассмотрении приёмов вы числений, а вопросом, имеющим самостоятельное значение. В конце изучения устных приёмов сложения повторно рассматр ивается уже известный детям приём перестановки слагаемых и вводится новый приём их группировки. Показывается, как использование того и другого приёма даёт возможность рац ионализировать вычисления в случае сложения нескольких слагаемых.

Наряду с устными приёмами вычислений рассматриваются письменные. Во 2 классе впервые происходит знакомство учащ ихся с записью сложения и вычитания столбиком при рассмо трении более сложных случаев вычислений в пределах 100. В этом проявляется усиление роли алгоритмов в курсе в целом.

С третьей четверти в порядке ознакомления вводится тема «Умножение и деление» (общие вопросы, умножение и деление с числами 2 и 3). Рассматривается конкретный смысл действий, названия их компонентов и результатов, переместительное свойс тво умножения, взаимосвязь между компонентами и результа том каждого действия, составляются и разучиваются таблицы с числами 2 и 3. Однако в основные требования к концу второго года обучения круг этих вопросов не входит. Этот материал дан в ознакомительном плане и подготавливает учащихся к усвоению основных вопросов следующего года обучения.

Как это и принято в системе упражнений, разработанных авторами, изучение арифметических вопросов связано с решением текстовых задач новых видов (на нахождение неизвестного слаг аемого, неизвестного уменьшаемого, неизвестного вычитаемого, на раскрытие смысла действий умножения и деления и др.). Идёт работа и над задачами в два действия, включающими изученные виды простых задач (на увеличение или уменьшение числа на не сколько единиц и нахождение суммы, на нахождение третьего слагаемого и др.).

Как и в 1 классе, используется краткая запись задачи, иллюс трирование её содержания с помощью геометрических фигур, практические действия с которыми являются, по сути, решением задачи. Такие схемы (или модели) можно использовать и для сос тавления текстовых задач самими детьми. Опора на схему при выборе действия для решения задачи возможна в тех случаях, когда числовые данные позволяют её составить (нарисовать). В дальнейшем, когда в задачах начинают фигурировать числа, которые больше 10, дети знакомятся с иллюстрированием зада чи с помощью чертежа.

На фоне вопросов, относящихся к рассмотрению арифметич еских действий, появляется ряд новых вопросов, на которые учи телю следует обратить внимание. Вводятся понятия о верных и неверных равенствах и неравенствах, новые термины выражение, значение выражения.

Для нахождения значения выражения в 1 классе учащиеся вып олняли действия в том порядке, как они записаны: слева на право. Во 2 классе вводятся скобки как знаки, указывающие на изменение порядка действий. Дети знакомятся с выражениями, содержащими переменную (вида b + 4, а – 6, 30 – с и др.), а также с понятиями уравнение и решение уравнения. Во 2 классе уравнения решаются способом подбора и фактически заменяют собой знакомые детям примеры с окошком. Способ подбора используется лишь тогда, когда решение уравнения находится лег ко, например на основе знания состава числа (30 + х = 39), а также на основе знания действий с числом 0 (28 + х = 28, 17 – х = 0). После усвоения взаимосвязей между суммой и слагаемыми, а также между уменьшаемым, вычитаемым и раз ностью на этой основе решаются уравнения вида х + 7 = 35, х – 13 = 20, 46 – х = 42.

Продолжается работа над величинами. В начале второго го да обучения даётся представление о новой единице длины — милл иметре. В течение всего учебного года учащиеся используют миллиметровую линейку при измерении и вычерчивании отрезков заданной длины. Более раннее введение миллиметра отвеча ет требованиям, которые предъявляются к умениям детей на урок ах трудового обучения. Помимо миллиметра, дети знакомятся с более крупной единицей длины — метром и усваивают соотношения между всеми известными им единицами длины (сантиметр, дециметр, миллиметр, метр).

Так же как и в учебнике для 1 класса, в данном учебнике уси лено внимание к формированию пространственных и геометрич еских представлений. Формируются представления о прямом, остром и тупом углах, прямоугольнике (квадрате). Рассматрива ются некоторые их свойства, и дети подводятся к определению понятий прямоугольник, квадрат, к выяснению отношений между ними. Вводятся термины длина ломаной и периметр многоугольника, в частности периметр прямоугольника (квад рата).

Система и методика рассмотрения в учебнике основных воп росов курса будут подробно изложены по темам в следующих разделах настоящего пособия. Здесь же отметим некоторые прин ципиальные изменения, внесённые в содержание и структуру учебника.

Значительно усилено в учебнике внимание к развитию дет ей, в частности к развитию их мышления, речи, познавательн ых способностей. В учебник включены специальные развивающ ие упражнения, в том числе игровые. Однако большие возможн ости развития учащихся заложены в системе основных заданий книги и в объяснительных текстах учебника.

Работе с текстом, которого в учебнике для 2 класса стало больше, следует уделять серьёзное внимание. Введение нового материала, точно сформулированные задания, пояснительные тек сты могут помочь учителю полноценно использовать учебник, углублять его обучающие и развивающие возможности, уточнять терминологию, словесные формулировки. Лаконичная, корректн ая речь учителя — залог успешного формирования краткой грамотной речи учащихся, которые сначала слушают образцы правильной математической речи, а затем сами употребляют корр ектные выражения. Но этого мало. Учебник как носитель грамотной математич еской речи должен оказывать воздействие не только опосредов анно, через учителя, но и напрямую. Для этого дети должны сами работать с текстом учебника, сначала отвечать на воп росы учителя, а позднее самостоятельно ставить вопросы и наход ить ответы на них в учебной книге. Необходимо побуждать детей обращаться к тексту учебника и на последних уроках 2 класса, не ограничиваться краткими ответами учеников, а пол ноценно использовать вместе с ними представленные справочные сведения, с помощью которых можно эффективно пос тигать учебный материал, уточнять теоретические и практичес кие вопросы.

Работа с учебником не исчерпывает всего содержания урока, так как, кроме него, используются демонстрации, практическая раб ота с дидактическим материалом, игры и др., поэтому учитель всегда может создать проблемную ситуацию, связанную с темой занятия. При этом вопрос перед детьми может быть поставлен, например, так, что ответить на него они смогут, если самостоя тельно прочитают текст в учебнике.

Нельзя забывать на уроках математики и об устном счёте — гимнастике для ума. Необходимый для этого материал содержитс я в основной части практически каждой страницы учебника. Сле дует иметь в виду, что много упражнений для устного счёта мож но найти и на полях учебника. Большинство из развивающих за даний, расположенных там, может быть с успехом использовано для развития вычислительных умений детей (цепочки, магические квадраты, числовые домики и др.).

Многие задания учебника позволяют учителю использовать их творчески, анализировать их с учётом реальных знаний и умений своих учеников и вносить в эти задания некоторые дополнения, усложняющие содержание (проанализировать примеры в столби ке и продолжить его составление, решая новые примеры; соста вить и решить аналогичную задачу или задачи, обратные данной; изменить вопрос задачи так, чтобы она решалась не одним, а двум я действиями или чтобы она решалась другим действием, и т. п.).

Задания в учебнике часто подобраны так, что учитель может проводить дифференцированное обучение. Более слаб ые ученики решают примеры в одно действие, содержащиеся в первых двух столбиках задания, более сильные — примеры в два действия из двух других столбиков; одни ученики решают задачу из учебника, другие составляют и решают задачу, обратную дан ной; одни записывают решение задачи выражением, другие, кот орым трудно, — по действиям и т. п. Полезно предлагать для самостоятельной работы несколько вариантов заданий разного уровня сложности, с тем чтобы учащиеся сами выбрали тот вариант, с которым они, по их мнению, могут справиться. Такая работа предполагает последующую проверку в классе.

Особо следует сказать о воспитательных возможностях, заложенных в учебнике. Самостоятельные наблюдения, сравнен ие, классификация предметов (явлений) по определённому приз наку, посильные обобщения, к которым учебник побуждает детей, формируют у них учебные мотивы, познавательный инт ерес вообще и, что очень важно, интерес к математике в частн ости, развивает личностные и познавательные универсальные учебные действия.

В настоящем пособии авторы дают характеристику основных нап равлений работы, а также приводят планируемые результаты освоения программы по математике второго года обучения. На примере подробных конспектов отдельных уроков показаны приёмы работы учителя. Система проверочных работ, содержащихся в пособии, облегчит учителю конт роль за усвоением детьми учебного материала.

В помощь учителю в конце настоящего пособия даётся примерное распределение материала по четвертям учебного года и по урокам. Пользуясь этим планированием и учитывая конк ретные условия обучения, а также уровень продвижения своих учеников, учитель может гибко строить работу, увеличивая или уменьшая число уроков, отведённых на изучение того или иного вопроса. В связи с этим учитель может варьировать работу, включая дополнительные упражнения как в любой урок по теме учебника, так и в те уроки, которые он будет проводить дополнительно. Учитель использует при этом дополнительные задания из разделов «Что узнали, чему научились», «Странички для любознательных», материал для закрепления всего прой денного (в конце учебника), а также многочисленные задания разв ивающего характера, приведённые на полях учебника практически каждой страницы учебника.

Следуя в своей работе за учебником, поурочное построение которого помогает организовать работу с помощью примерного распределения материала по четвертям и урокам, рекомендованн ого настоящим пособием, а также творчески выстраивая резервн ые уроки, учитель гарантированно обеспечит необходимый уро вень развития детей и своевременное овладение ими на треб уемом уровне тем материалом, который соответствует про грамме второго года обучения в начальной школе.

Учебник математики для 2 класса издаётся в комплекте с другими учебными пособиями.

Дополнением к учебнику является «Рабочая тетрадь по математике» авторов М. И. Моро, С. И. Волковой (в 2 частях для первого и второго полугодия). Материал тетради привязан к урокам учебника, что облегчает учителю задачу её использования на каждом уроке. Содержание тетради направлено на поддержание основной методической линии учебника, в которой делается акцент на развитие у учащихся универсальных учебных действий в процессе овладения программным материалом.

Пособие для учащихся «Математика. Проверочные работы. 2 класс» (автор С. И. Волкова) содержит тексты проверочных работ, составленных по отдельным вопросам тем, и предметные тесты, обеспечивающие тематическую проверку учебного материала. В пособии созданы условия для реализации такого важного компонента учебной деятельности, как формирование и развитие у учащихся действий самоконтроля и самооценки предметных результатов изучения основных тем курса. Использование пособия обеспечивает формирование личностных и регулятивных универсальных учебных действий.

Пособие для учащихся 2 класса «Математика. Тесты» (автор С. И. Волкова) содержит тесты по математике, составленные в соответствии с содержанием курса «Математика» авторов М. И. Моро и др. Тестовые задания разработаны ко всем учебным темам каждого года обучения и включают задания базового и повышенного уровней сложности. Задания базового уровня представлены тремя видами тестов. При этом обеспечивается постепенное нарастание сложности заданий как внутри каждого теста, так и при переходе от одного вида тестов к другому. Пособие позволит учителю получить  информацию об уровне усвоения учащимися учебного материала по отдельным вопросам изученной темы, по всей теме и по всему курсу математики второго года обучения.

Пособие для учащихся 2 класса «Математика. Тетрадь учебных достижений» (автор С. И. Волкова) поможет выявить достижение учащимися предметных и метапредметных результатов обучения с помощью специальной системы заданий и инструментов самодиагностики и самооценки. Предлагаемые в пособии задания в большей степени направлены на формирование и развитие регулятивных универсальных учебных действий. В пособии приведены инструменты для самопроверки выполнения работ («Ключи к заданиям»), таблицы «Мои результаты» для самооценки каждой работы и по итогам каждого полугодия.

Кроме того, разработано «Математика. 2 класс. Электронное приложение к учебнику М. И. Моро» (линия учебников авторов М. И. Моро и др.). На дисках представлен учебный материал для самостоятельной работы учащихся как на уроках математики (при введении нового материала, при закреплении, при проведении учащимися самоконтроля), так и в домашних условиях.

Пособие «Математика. Устные упражнения. 2 класс» (автор С. И. Волкова) адресовано учителю и содержит материал, который окажет помощь учителю в наиболее эффективной организации и проведении на уроках математики устных упражнений с целью закрепления, систематизации и обобщения изученного материала.

В пособии к каждому уроку учебника даётся набор устных упражнений, полностью соответствующих целям урока и изучаемому материалу. Материал пособия представляет дополнительные задания для развития личностных и познавательных универсальных учебных действий.

Пособие для учащихся 2 класса «Для тех, кто любит математику» (авторы М. И. Моро, С. И. Волкова) содержит задания повышенного уровня сложности. Пособие может частично использоваться на уроках математики для организации дифференцированного обучения, а частично во внеурочной работе, например для организации работы математического кружка познавательной направленности.

Для организации внеурочной познавательной деятельности учащихся учитель может также использовать программу факультативного курса «Математика и конструирование» для 2 класса и соответствующее пособие «Математика и конструирование» (автор С. И. Волкова).

ОСОБЕННОСТИ СТРУКТУРЫ И СОДЕРЖАНИЯ УЧЕБНИКА

Описание содержания

и структуры учебника

В учебнике для 2 класса продолжена и расширена содержательная линия задач и заданий поискового и творческого характера, начатая в 1 классе, но уже на новом числовом и содержательном материале. Это позволило усилить математическую базу для целенаправленного формирования у учащихся универсальных учебных действий, развития у детей приёмов умственной деятельности, формирования умений применять математические знания при решении задач практического характера, формирования творческого отношения к учебной деятельности, развития пространственного воображения и речи учащихся. Эти задания, как и в учебнике 1 класса, размещены в специальной рубрике «Странички для любознательных».

Использование заданий этой рубрики позволит продолжить и во 2 классе работу по развитию у детей приёмов умственной деятельности и будет способствовать:

•         развитию логического мышления при выполнении заданий на проведение сравнения, анализа, синтеза и классификации объектов, на применение аналогии и обобщения, на построение цепочки логических рассуждений и логических выводов, на применение знаний в изменённых условиях;

•         формированию у учащихся основ компьютерной грамотности, в частности, развитию основ алгоритмического мышления: умения составлять план действий и реализовывать его для решения поставленной учебной задачи, проводить пошаговый контроль; с этой целью предлагаются задания, направленные на вычерчивание (продолжение) узора по образцу, по заданному плану, составление плана, по которому начерчен узор, и др.;

•         продолжению работы с условной Вычислительной машиной и работы на Вычислительной машине по заданному алгоритму;

•         продолжению работы по уточнению понятий «все», «каждый» и знакомству с элементами и языком логики высказываний «если…, то…», «если не…, то…» и др.;

•         решению заданий, направленных на развитие пространственного воображения и конструкторских умений;

•         решению задач-расчётов, направленных на формирование умений применять полученные знания для решения задач практического содержания, прогнозировать результат, делать прикидку, понимать смысл информации, представленной в таблице, дополнять таблицу недостающей информацией;

•         развитию коммуникативных умений, в частности при участии в математических играх, предполагающих проведение математических расчётов, обеспечивающих успешное завершение игры, формируется умение работать в паре.

В учебнике представлен материал, предполагающий сбор и обработку информации при выполнении проектной деятельности в рубрике «Наши проекты». По теме «Математика вокруг нас» разработано два проекта: первый — «Узоры и орнаменты на посуде» (ч. 1, с. 48, 49), второй — «Оригами» (ч. 2, с. 36, 37).

Как видно из приведённого описания, расширение содержания учебного материала создаёт дополнительные условия для формирования личностных (материал вызывает интерес к изучению математики, усиливает познавательную активность и мотивацию к изучению предмета), познавательных (формирует умения работать с информацией, создаёт дополнительные возможности для развития логического и алгоритмического мышления, пространственного воображения), коммуникативных (представляет основу для приобретения опыта работы в паре, в группе, формирует умения общаться со сверстниками) универсальных учебных действий.

Структура учебника сохранила тематическое и поурочное построение, однако значительные изменения претерпело как построение и оснащение учебных тем, так и структура каждого урока.

В учебнике реализуется системно-деятельностный подход. Каждый урок построен в соответствии с основными компонентами учебной деятельности и включает в себя:

•    познавательную цель урока;

•    учебный материал для достижения поставленной цели; • задания для первичного закрепления новых знаний;

•    математический материал для повторения ранее изученного;

•    задания для проведения учащимися самоконтроля и самооценки результатов своей учебной деятельности на этом уроке (такие задания расположены под красной чертой и отмечены значком).

Познавательные цели урока представлены в учебнике в разной форме: при введении нового материала это формулировки, которые настраивают учащихся на поиск новых свойств, отношений, алгоритмов и др., например «Будем учиться…», «Узнаем, как…», в некоторых случаях в форме проблемных вопросов, ответы на которые требуют установления связей между тем, что уже известно второклассникам, и тем, что они ещё не знают (это показывает необходимость расширения имеющихся знаний), например при применении правил сложения и вычитания в новых условиях «Объясни, как выполнено действие, и найди способ, как выполнить действие уже в новых условиях», в случаях, когда очень важна активизация конкретных знаний, учащимся предлагается повторить материал, который подготавливает изучение нового.

Это выполняется с помощью специально представленных в учебнике устных заданий или задания найти соответствующий материал в справочнике. В каждом случае перед учащимися ставится учебная задача, которую они должны понять, принять и сохранить в течение всего урока, а в конце урока самостоятельно проверить, как они справились с усвоением нового материала урока, — провести самоконтроль и самооценку результатов своей учебной деятельности на уроке по заданиям, предложенным в учебнике или по материалам пособия «Проверочные работы».

Структура каждой темы в учебнике соответствует той же логике, по которой построен каждый урок. Изложение темы открывается шмуцтитулом — специальной страницей, на которой, кроме названия темы, приведены учебные цели и планируемые предметные результаты её изучения. Далее следует содержательное поурочное изложение основных вопросов названной темы, а в конце её сначала даётся материал рубрики «Что узнали. Чему научились», направленный на повторение, систематизацию и обобщение изученного в теме, а после него в рубрике «Проверим себя и оценим свои достижения» представлен материал для самопроверки и самооценки учащимися достигнутых ими предметных результатов по основным вопросам изученной темы. Материал этой рубрики представлен в форме предметных тестов  по математике с выбором правильного ответа из трёх предложенных, среди которых всегда есть правильный. Тестовая форма самопроверки даёт возможность наиболее полно охватить изученные в теме вопросы.

Такое построение в учебнике основных программных тем второго года обучения математике создаёт условия для достижения учащимися личностных и метапредметных результатов.

Отметим, что в конце учебника (ч. 2, с. 102—109) приведён материал для итогового повторения «Что узнали, чему научились во 2 классе» и задания для проверки своих знаний по всему году обучения «Проверим себя и оценим свои достижения», которые логически завершают структуру, принятую в учебнике внутри каждой темы.

Материал рубрики «Что узнали, чему научились во 2 классе» представлен по основным программным темам второго года обучения «Числа от 1 до 100»: «Нумерация»;

«Числовые и буквенные выражения»; «Равенство. Неравенство. Уравнение»; «Сложение и вычитание»; «Решение задач»; «Длина отрезка. Единицы длины»; «Геометрические фигуры».

В силу этого учитель сам определяет структуру уроков повторения: он может выстроить урок, следуя логике изложения материала в рубрике, или спланировать урок, отбирая материал из каждой темы.

Достижение личностных

и метапредметных результатов

Расширенное содержание и структура учебника 2 класса создают базу для достижения учащимися как определённых программой предметных результатов обучения математике, так и личностных и метапредметных результатов.

Несмотря на то что курс математики больше направлен на достижение предметных и метапредметных результатов, в нём уделяется большое внимание достижению личностных результатов, которое осуществляется в основном за счёт работы с текстовыми задачами со специально подобранными сюжетами и иллюстрациями.

В курсе размещён материал, который помогает:

1)       продолжить работу по формированию уважительного отношения к семейным ценностям, бережного отношения к окружающему миру, здоровому образу жизни.

Это обеспечивается включением в учебник текстовых задач, сюжеты которых раскрывают добрые отношения между членами семьи, рассказывают о помощи детей по хозяйству, об общих делах в семье, о помощи детей в озеленении города, об уходе за животными и птицами, об участии в спортивных секциях (ч. 1: с. 9, № 5; с. 12, № 6, 7; с. 24, № 4; с. 26, № 5; с. 39, № 5; с. 43, № 5; с. 45, № 8; с. 47, № 6, 7; с. 52, № 3; с. 85, № 7 и др.; ч. 2: с. 6, № 3; с. 10, № 1, 2, 3; с. 11, № 8; с. 17, № 4; с. 26, № 35; с. 30, № 2; с. 62, № 2; с. 65, № 4 и др.).

Кроме того, сюжеты перечисленных задач задают направленность текстам задач при их составлении;

2)       продолжить формировать первоначальные представления о целостности окружающего мира, о возможности моделировать (сначала практическим способом, а затем на схематических рисунках и схематических чертежах) отношения между объектами окружающего мира.

Этот результат закладывается в ходе освоения приёма моделирования (практического, в форме схематических рисунков и схематических чертежей) при изучении многих разделов курса математики 2 класса: нумерации, конкретного смысла арифметических действий умножения и деления, при работе с текстовыми задачами, при выполнении заданий геометрического содержания, при сборе информации и определении формы её представления.

Так, если в 1 классе тексты простых задач сопровождаются предметными и схематическими рисунками, то во 2 классе к ним добавляются схематические чертежи, что вызвано значительным расширением области рассматриваемых в курсе чисел; запись решения задачи выполняется в разной форме, в том числе с помощью числового выражения (ч. 1: с. 28, № 1; с. 29, № 1; с. 39, № 5, 6;  с. 43, № 5; с. 46, № 4, 5; с. 64, №  1; с. 65, № 1, 2; с. 73, № 9; ч. 2: с. 48, № 1; с. 49, № 1, 2; с. 53, № 5;

с. 56, № 2;  с. 59, № 2; с. 60, № 1; с. 61, № 2; с. 66, № 12; с. 82, № 2).

Особую ценность в плане формирования основ целостного восприятия мира имеют задания, в которых ученики по заданному схематическому чертежу к задаче или записи выражения для её решения сами составляют текстовую задачу. В этом случае схематический чертёж один (решение одно), а составленных задач много, важно только, чтобы сохранялись заданные на чертеже или в решении отношения между объектами, задействованными в тексте составленной задачи (составление задач по схематическому чертежу (ч. 1: с. 29, № 2; с. 56, № 31; с. 89, № 4; с. 93, № 31; ч. 2: с. 44, № 31; с. 59, № 2); по решению задачи или по выражению для её решения (ч. 1: с. 38, № 4; с. 66, № 6; ч. 2: с. 9, № 4; с. 32, № 3; с. 34, № 6;

с. 44, № 30; с. 48, № 3; с. 49, № 4; с. 55, № 3; с. 62, № 4; с. 63, № 9; с. 84, № 7; с. 90, № 3).

Это достаточно наглядно подчёркивает универсальность математического способа моделирования и записи решения на языке математики;

3) продолжить формирование мотивов учебной деятельности и личностного смысла учения, развивать интерес к обучению, познанию, расширению знаний, учебному предмету «Математика».

Учебник построен поурочно. Каждый урок выстраивается в соответствии с требованиями системно-деятельностного подхода, что даёт возможность показать учащимся недостаточность имеющихся у них знаний для достижения поставленной познавательной цели и тем самым мотивирует их на поиск новых знаний и способов действий, на расширение знаний, придаёт поиску новых знаний личностно значимый смысл для каждого ученика. Такое построение учебника повышает активность ребёнка в процессе обучения, способствует формированию умения самостоятельно добывать новые знания, а затем проводить самоконтроль и самооценку результатов своей учебной деятельности на уроке.

Такая структура урока позволяет повысить личностную мотивацию каждого ученика в успешной деятельности на уроке. Систематическое использование материала для самоконтроля даёт ему возможность из урока в урок отслеживать результаты продвижения при изучении темы, корректировать их, а всё вместе поможет заложить основу для формирования впоследствии рефлексивной самооценки, личностной заинтересованности в приобретении и расширении знаний и способов действий, для развития умения анализировать свои действия, а позднее и управлять ими, положительно влияя на развитие личностной саморегуляции.

Материал учебника по математике для 2 класса позволяет обеспечить достижение следующих метапредметных результатов.

Регулятивные:

1)       Понимать, принимать и сохранять учебную задачу, соответствующую этапу обучения, и решать её в сотрудничестве с учителем, ориентироваться в учебном материале, представляющем средства для её решения.

Достижению этого результата способствует обновлённая структура учебника для 2 класса, реализующая размещение на специальных страницах (шмуцтитулах: ч. 1: с. 3, 25; ч. 2: с. 3, 47) название темы, цели её изучения и планируемые предметные результаты. Это помогает учащимся не только понимать и принимать поставленную учебнопознавательную цель, но и  достаточно продолжительное время (на протяжении изучения всей темы) сохранять её. Эта структурная особенность учебника поддерживается и усиливается структурой каждого урока, которая включает в себя постановку учебной задачи и представляет содержательный материал для учебной деятельности, направленной на её решение.

Такое построение учебника позволяет ученикам, принимая и сохраняя учебные цели каждого урока, видеть перспективу изучения темы и соотносить конкретные цели каждого урока с конечными целями её изучения.

Формирование умений искать и находить способы решения учебных задач обеспечивается рекомендованными в учебнике способами действий: «Сравни», «Объясни», «Определи, по какому правилу…», «Объясни по плану», «Вычисли и проверь» и др. (ч. 1:  с. 12, 14, 20, 34, 44, 45, 57, 59, 60 — 62, 66 — 69, 75, 78 и др.; ч. 2: с. 12, 13, 16 — 19, 29 и др.).

2)       Составлять под руководством учителя план действий для решения учебных задач, выполнять план действий и проводить пошаговый контроль его выполнения в сотрудничестве с учителем и одноклассниками.

В учебник для 2 класса включён математический материал, направленный на формирование у учащихся умения планировать учебные действия. Учащиеся составляют:

•         план решения текстовых задач (ч. 1: с. 33, № 5, 6; с. 41, № 2; с. 43, № 5; с. 53, № 10, 11; с. 55, № 24, 1), № 27; с. 58, № 3; с. 59, № 2; с. 62, № 3; с. 65, № 1 и др.; ч. 2: с. 16, № 4; с. 19, № 2; с. 23, № 13; с. 24, № 21; с. 25, № 28, 31; с. 26, № 36; с. 44, № 28; с. 45, № 35; с. 76, № 2 и др.);

•         план выполнения алгоритмов сложения и вычитания чисел в пределах 100 (ч. 2: с. 4, 5, 12, 13, 16, 19; с. 25, № 24; с. 34, № 5 и др.);

•         план вычерчивания узоров (ч. 1: с. 56, № 36; с. 75, № 29; ч. 2: с. 28, № 3);

•         план работы на условной Вычислительной машине

(ч. 1: с. 51, № 4; ч. 2: с. 28, № 2; с. 39, № 5; с. 87, № 6);

•         план стратегии успешной игры (ч. 1: с. 19, № 4;

с. 71, № 5; ч. 2: с. 65, № 6).

3) Проводить (на начальном уровне) самоконтроль и самооценку результатов своей учебной деятельности, описывать результаты учебных действий, используя записи и математические термины.

Как уже было сказано, структура уроков, разработанных в учебнике, такова, что обязательным элементом каждого урока является материал для самоконтроля и самооценки результатов учебной деятельности. Каждая учебная тема заканчивается рубриками «Что узнали. Чему научились» и «Проверим себя и оценим свои достижения», содержание которых согласовано с целевыми установками, сформулированными на шмуцтитуле по теме.

Кроме того, в конце учебного года в рубрике «Тексты для контрольных работ» предлагаются задания двух уровней: базового и повышенной сложности, которые выбирает ученик на основе самооценки результатов своей учебной деятельности в течение года. Предложенная структура учебника и её содержательное наполнение позволяют формировать у учащихся первоначальные навыки проведения поурочного, тематического и итогового самоконтроля и самооценки результатов учебной деятельности на разных этапах изучения основных тем курса, способствуя в дальнейшем формированию и развитию основ саморегуляции.

Познавательные:

1) Осуществлять поиск нужной информации в учебнике и в других источниках (книги, аудио- и видеоносители, а также используя Интернет с помощью взрослых) и представлять собранную информацию в разной форме

(пересказ, текст, таблица).

Формирование умения осуществлять  поиск  информации, необходимой для выполнения задания, работать с ней и представлять её в разных формах в учебнике для 2 класса обеспечивается как на каждом уроке, так и при работе с задачами творческого и поискового  характера, в которых учащиеся знакомятся с табличной формой представления информации:

•         чтение и заполнение таблиц недостающими элементами, раскрывающих взаимосвязь между компонентами и результатами действий сложение и вычитание (ч. 1:

с. 53, № 14; с. 54, № 19; с. 72, № 8; с. 74, № 21; с. 81, № 3 и др.; ч. 2: с. 6, № 6; с. 7, № 5; с. 9, № 7; с. 17, № 7 и др.); конкретный смысл действия умножение (ч. 1: с. 47); взаимосвязь между компонентами и результатом действия умножение (ч. 2: с. 55, № 1; с. 76, № 4; с. 85, № 5 и др.); содержащих определённую закономерность построения, которую надо установить и в соответствии с которой надо определить и устно описать, какими элементами должны быть заполнены свободные ячейки таблицы (ч. 1: с. 81, № 8; с. 90, № 9);

•         чтение несложных таблиц, умение понимать смысл и извлекать информацию, представленную в каждой ячейке, строке, столбце таблицы (ч. 1: с. 24, № 4; с. 85, № 7; ч. 2: с. 11, № 8);

•         запись решения задачи в таблице, когда задача имеет не одно, а несколько решений (ч. 2: с. 43, № 26; с. 68, № 33);

•         чтение таблиц, в которых заложен ключ к шифру для выполнения задания (ч. 1: с. 43, № 8).

Поиск информации в различных источниках (в книгах, журналах, Интернете, в беседах со взрослыми и др.) осуществляется учащимися при выполнении заданий рубрики «Наши проекты». При  этом учащиеся не только отыскивают и собирают информацию, но и проводят её анализ и систематизацию по основаниям, приемлемым для используемых в проекте объектов. Так, например, при сборе материала для проекта «Математика вокруг нас. Узоры и орнаменты на посуде» (ч. 1: с. 48, 49) систематизировать собранную информацию дети могут по разным основаниям: по видам посуды или по видам используемых узоров и орнаментов для её украшения (растительные узоры и орнаменты, геометрические узоры и др.).

2)       Освоить под руководством учителя способы решения задач творческого и поискового характера.

Освоение таких способов и приёмов действий начато в 1 классе. Во 2 классе оно продолжается, получает своё развитие и обеспечивается специально подобранной серией задач и заданий на новом содержательном математическом материале (используется расширенная область чисел, новые отношения между объектами, новые приёмы действий и т. д.).

Задачи этого вида представлены в рубрике «Странички для любознательных» (ч. 1: с. 18, 19, 24,  36, 37, 50, 51, 70, 71; ч. 2: с. 20, 21, 28, 38, 39, 64, 65, 86, 87).

Выполняя эти задания, учащиеся расширяют свой опыт решения задач творческого и поискового характера, учатся находить нестандартные способы действий, применять полученные знания в изменённых условиях, решать несложные задачи-расчёты практического и прикладного содержания.

3)       Уметь использовать освоенные знаково-символические средства и способы действий для решения несложных учебных задач, для создания моделей изучаемых объектов, в том числе и при решении текстовых задач.

Начиная с 1 класса дети учатся использовать математические знаки и символы для записи различных ситуаций, одновременно с этим правильно читать математические записи, учатся использовать наглядные модели (предметные рисунки, схематические рисунки, чертежи), отражающие количественные и пространственные отношения между объектами, начинают овладевать приёмом моделирования. Эта работа продолжается и во 2 классе: учащиеся овладевают новыми математическими символами и знаками, новыми понятиями и математическими терминами, свойствами чисел, величинами и новыми единицами их измерения, новыми геометрическими фигурами и их изображениями.

Развитие у учащихся умений моделировать отношения между объектами продолжается во 2 классе при работе с разнообразными текстовыми задачами. Во 2 классе расширяется область рассматриваемых чисел, что влечёт за собой необходимость введения схематических чертежей вместо ранее освоенных схематических рисунков (ч. 1: с. 29, № 1, 2 и др.).

Способ моделирования ученики используют и при решении задач повышенной сложности (ч. 1: с. 17, № 6; с. 27, № 7; с. 28, № 5 и др.; ч. 2: с. 20, № 2 и др.).

В учебнике системно выстраиваются задания, направленные на овладение способом моделирования при введении новых для учащихся арифметических действий умножение и деление. Детям предлагается выстроить математическую  схематическую модель некоторого фрагмента реальной действительности (ч. 2: с. 48, № 1; с. 49, № 1, 2; с. 51, № 1, 2; с. 53, № 5; с. 58, № 1; с. 59, № 1, 2; с. 60, № 1; с. 61, № 2 и др.), выявить её особенности и свойства, провести их описание на языке математических символов и знаков.

Параллельно с арифметическим вводится геометрический материал, развивающий и уточняющий пространственные представления детей. Во 2 классе уточняется понятие ломаной, рассматриваются способы определения длины ломаной и периметра многоугольника, вводятся виды углов: прямой, острый, тупой, среди четырёхугольников выделяется прямоугольник, а среди прямоугольников — квадрат, рассматривается свойство противоположных сторон прямоугольника.

Этот геометрический материал сопровождается серией заданий на деление фигуры на заданные части, на составление фигур заданного вида из предложенных фигур-частей, что позволяет развивать у учащихся пространственное воображение и математическую речь, а также умение моделировать пространственные отношения. 4) Учиться излагать своё мнение и аргументировать его осуществляется за счёт включения в учебник заданий, способствующих созданию ситуаций, когда учащиеся ставятся перед выбором и обоснованием наиболее удобного способа выполнения задания или способов решения текстовой задачи (ч. 1: с. 32, № 1; с. 34, № 1 и др.; ч. 2: с. 22, № 5; с. 27, № 40; с. 31, № 2; с. 72, № 4; с. 76, № 3 и др.); в случаях, когда учащимся предлагается провести рассуждение, высказать своё мнение и обосновать его (ч. 1: с. 14, № 3; с. 41, № 3; с. 42, № 4; с. 45, № 3, 1 и др.; ч. 2: с. 33, № 1, 8; с. 35, № 1, 2), № 7; с. 51, № 1, 3 и др.).

5) Овладевать логическими действиями сравнения, анализа, синтеза, обобщения, классификации по разным признакам на математическом материале учебника для 2 класса.

Достижение этих результатов обеспечивается серией таких заданий учебника, как «Рассмотри…», «Сравни, не вычисляя», «Найди лишний…», «Выбери правильный ответ», «Выбери решение задачи», «Найди и исправь ошибки», «Расставь скобки так, чтобы значение выражения стало равно заданному числу», «Составь фигуру (объект) из предложенных частей», «Раздели геометрическую фигуру на заданные части» и др. В учебнике предлагаются также задания, в которых учащимся предстоит:

•         установить закономерность следования ряда объектов (чисел, числовых выражений, значений величин, геометрических фигур и т. п.), продолжить его или дополнить недостающими элементами по найденному правилу (ч. 1: с. 8, № 8; с. 26, № 4; с. 53, № 9; с. 63, № 6; с. 75, № 28; с. 78 (поля); с. 81 (поля); с. 83, № 6; ч. 2: с. 11, № 9; с. 13 (поля); с. 21, № 5; с. 25 (поля); с. 27, № 41; с. 38, № 1; с. 48 (поля); с. 87, № 4, 7);

•         провести классификацию объектов (найти лишний объект): чисел, равенств, числовых выражений, геометрических фигур по разным признакам (ч. 1: с. 4 (поля); с. 21 (поля); с. 35, № 9; с. 39, № 7; с. 46, № 3; с. 60 (поля); с. 69 (поля);

с. 91, № 12; ч. 2: с. 12, 29, 31, 58, 59 (задания на полях); • применить знания в изменённых условиях (ч. 1:

с. 36, № 1; с. 37, № 3; с. 47, № 8; с. 54, № 20; с. 71, № 4;

ч. 2: с. 20, № 1; с. 64, № 3; с. 65, № 4; с. 66, № 16; с. 67,

№ 25; с. 75, № 6; с. 86, № 2; с. 87, № 5);

•         проводить логические рассуждения, выстраивать цепочку логических рассуждений и делать выводы (ч. 1:

с. 26, № 5; с. 45, № 8; с. 51, № 2; с. 55, № 29; с. 75, № 27; с. 89, № 7; ч. 2: с. 20, № 2; с. 38, № 2; с. 39, № 4; с. 45, № 35; с. 84, № 9; с. 86, № 1; с. 93, № 8).

6) Овладевать базовыми предметными и межпредметными понятиями, отражающими существенные связи и отношения между объектами, явлениями и процессами.

Обновлённые содержание и структура учебника обеспечивают освоение второклассниками важнейших (базисных) понятий начального курса математики: число, величина, геометрическая фигура. Во 2 классе расширяется область изучаемых чисел от 0 до 100. Учащиеся научатся:

•         образовывать, называть, записывать, сравнивать числа от 0 до 100, выполнять действия с числами (увеличивать/уменьшать число на несколько единиц); познакомятся с новыми единицами длины: миллиметр и метр;

•         выполнять устно и письменно действия сложения и вычитания с двузначными числами в пределах 100 с использованием таблицы сложения и алгоритмов письменного сложения и вычитания;

•         устанавливать зависимости между объектами (величинами), представленными в задаче, планировать ход решения задачи, выбирать и объяснять выбор действия;

•         выделять из четырёхугольников прямоугольники, из прямоугольников квадраты;

•         измерять длину отрезка в заданных и самостоятельно выбранных единицах; находить длину ломаной и периметр многоугольника;

•         читать несложные готовые таблицы.

Коммуникативные:

Во 2 классе продолжается формирование умений учащихся работать в паре, в группе, в том числе принимать участие в обсуждении поставленной учебной задачи или при выполнении конкретных заданий, решении текстовых задач и т. п. в сотрудничестве с учителем и с одноклассниками, по-разному фиксировать результаты этих действий: в форме устного сообщения с использованием математической терминологии, с помощью схематических рисунков, схематических чертежей, математических записей.

Принимать активное участие в работе пары и группы: определять общие цели работы, намечать способы их достижения, договариваться о распределении ролей и обязанностей в совместной работе, вести диалог с одноклассниками, анализировать ход и результаты проделанной работы.

На достижение этого результата направлены:

•         предложенные в учебнике многочисленные задания, предполагающие работу в паре: «Цепочки», «Магические квадраты», «Занимательные рамки», «Набери заданное число» (числовые домики), «Круговые примеры», работа на условной Вычислительной машине, а также предметные тесты вида «Верно?», «Неверно?», размещённые в рубрике «Помогаем друг другу сделать шаг к успеху»;

•         серия математических игр «Составим поезд» (ч. 1, с. 15), «Поднимись по лесенке» (ч. 1, с. 16), «Кто первым наберёт 10» (ч. 1, с. 19), «Найди путь» (ч. 1, с. 70) и др.;

•         специально разработанные темы для организации проектной деятельности учащихся: «Математика вокруг нас. Узоры и орнаменты на посуде» (ч. 1, с. 48, 49) и «Оригами» (ч. 2, с. 36, 37), размещённые в рубрике «Наши проекты».

МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ РАБОТЫ С УЧЕБНИКОМ

В пособии представлен курс математики второго года обучения, который реализован в учебнике «Математика. 2 класс», переработанном в соответствии с требованиями ФГОС НОО. Именно поэтому в этой главе сначала излагаются методические подходы к работе с новым материалом и обновлённым элементам учебника, включение которых усиливает линию, направленную на формирование и развитие универсальных учебных действий (личностных, познавательных, регулятивных и коммуникативных), затем подробно рассматриваются методические подходы, обеспечивающие достижение предметных и метапредметных результатов обучения во 2 классе.

Реализация системно-деятельностного подхода

Учебник для 2 класса, как и учебник для 1 класса, построен поурочно, и в нём реализуется системно-деятельностный подход, отражённый в структуре каждого урока, его содержании и в обучении математике в целом, благодаря чему созданы  условия для активного включения каждого ученика в процесс обучения. Это позволяет обеспечить высокий уровень достижения предметных результатов,  а также формирование и развитие перечисленных универсальных учебных действий.

Основными элементами структуры каждого урока, разработанного в учебнике, являются:

•         постановка учебно-познавательной цели урока;

•         учебный материал в форме специально подобранных заданий, выполняя которые учащиеся подходят к самостоятельному (или частично самостоятельному) получению новых результатов (чисел, свойств, отношений, способов действий и др.);

•         задания для первичного закрепления нового материала, предполагающие сначала проговаривание вслух новых терминов, свойств, алгоритмов, способов действий и др. (внешняя речь), и одновременную математическую запись по новому материалу (например, выполнение задания с комментированием), а затем и самостоятельное выполнение предложенных заданий (с проговариванием про себя);

•         учебный материал для повторения и закрепления ранее изученного, а в отдельных случаях задания, направленные на достаточно длительную подготовку учащихся к введению нового материала;

•         учебный материал для проведения учащимися действий самоконтроля и самооценки.

Как и в 1 классе, каждый урок в учебнике начинается с постановки учебно-познавательной цели (задачи), которая требует определённой деятельности ученика для её достижения. В 1 классе дети освоили предлагаемую в учебниках структуру урока, в частности осознали, что каждый урок начинается с постановки той учебной задачи, которую им предстоит решать на этом уроке, научились понимать и  принимать поставленную учебную задачу, точную формулировку которой, как правило, давал учитель. Используя накопленный учащимися опыт и сохраняя проблемную форму постановки учебной задачи, во 2 классе учитель продолжает работу в этом направлении: добивается самостоятельных и более точных  формулировок учащимися учебно-познавательных целей урока (Что хотим узнать на уроке?), организует (под руководством учителя) обсуждение вариантов достижения поставленной цели, начинает формировать умение планировать свои действия в соответствии с поставленными учебными задачами (это касается целого ряда тем 2 класса, а именно: «Сложение и вычитание чисел в пределах 100», «Проверка сложения и вычитания», «Решение составных текстовых задач», «Длина ломаной» и др.), помогает учащимся определить, хватит ли их знаний для решения учебной задачи. Это поможет учащимся более осознанно принимать учебную задачу, сохранять её, будет ориентировать на поиск различных способов её решения. Чтобы эта деятельность стала  наиболее продуктивной, необходимо сделать поставленную познавательную цель личностно значимой для каждого ученика, заинтересовать в её достижении. Наиболее эффективной в этом плане является постановка цели в форме проблемного вопроса или проблемной ситуации, которая как раз и позволяет, с одной стороны, опереться на имеющиеся у детей знания, а с другой — подчёркивает недостаточность этих знаний для выполнения задания. После сформулированной познавательной цели в учебнике приводится материал и определяются  действия, выполняя которые ученики под руководством учителя подходят к решению поставленной задачи. Набирая из урока в урок опыт понимания, принятия и сохранения в течение всего урока поставленной задачи, ребёнок постепенно понимает важность нового знания и аккумулирует умения эти знания «открывать».

Остановимся более подробно на раскрытии методических подходов к постановке учебных задач урока. Формулировка учебно-познавательных целей урока в учебнике даётся в разной форме: «Будем учиться…», «Узнаем, что…», «Узнаем, как…», в форме проблемных вопросов, например: «Как выполнить вычисления вида…?», «Объясни, как…» и др. — или в форме, которая предполагает повторение ранее изученного и активизацию имеющихся по этому вопросу знаний для введения и усвоения нового «Вспомни и расскажи…». Но в каждом случае основная методическая задача учителя состоит в том, чтобы выстроить такую систему дополнительных заданий и подводящих вопросов, которая поможет учащимся сформулировать учебную задачу. Это поможет ученикам принять, осмыслить и сохранить учебную задачу на протяжении всего урока, повысит мотивацию поиска её решения, а результат решения поставленной учебной задачи станет личностно значимым для каждого ребёнка.

Так, например, на первом уроке, на котором учащиеся знакомятся с алгоритмом письменного сложения двузначных чисел в пределах 100 и у них формируется умение письменно выполнять это арифметическое действие (ч. 2, с. 4), учебно-познавательная цель сформулирована сразу для четырёх уроков: «Узнаем правила письменного выполнения сложения и вычитания. Будем учиться применять их в вычислениях».

Отметим, что сознательное освоение и применение алгоритмов письменного сложения и вычитания требует знаний:

•                     разрядного состава двузначных чисел;

•                     соотношения разрядных единиц (1 дес. — 10 ед.);

•                     табличных случаев сложения и вычитания в пределах 20.

Именно на выявление степени сформированности данных знаний и должна быть направлена серия заданий, включённых учителем в этап актуализации опорных знаний. Это могут быть задания на повторение:

1)       состава чисел в пределах 10. На доске заранее записаны числа 6, 9, 8, 7, 5. Учитель показывает указкой на одно из чисел, а ученики поднимают две карточки с числами, сумма которых равна заданному числу. Обсуждаются все возможные варианты;

2)       десятичного состава двузначного числа: «Из записанных на доске цифр (пункт 1) составь и запиши в порядке возрастания / убывания 4 двузначных числа, в каждом из которых содержится 8 дес. (7 дес. и т. д.)»;

3)       устных приёмов сложения и вычитания чисел в пределах 100. Учитель заранее записывает на доске два столбика примеров и вразброс ответы к ним:     

72 + 3                            54 + 10         Ответы: 68, 64, 73, 75, 63, 77

61 + 2            75 + 2 48 + 20     23 + 50

и предлагает ученикам записать в тетради примеры

в том порядке, в каком расположены ответы к ним.

— Чем похожи вычисления в первых трёх равенствах?  (Второе слагаемое содержит только десятки, и при вычислении  десятки прибавляли к десяткам.)

— Чем похожи вычисления в остальных равенствах?  (Второе слагаемое содержит только единицы и при вычислении единицы прибавляли к единицам.)

— На какие две группы можно разбить все записанные  на доске ответы? (Эти числа можно разбить на две группы по числу десятков в каждом из них: 68, 64, 63 и 73, 75, 77.)

Организовать работу по постановке учебной задачи для данного урока можно по-разному, например так. Учитель записывает на доске выражение 53 + 34 и предлагает детям подумать и рассказать, как можно найти его значение. С помощью абака и счётных палочек учитель показывает устный приём вычислений для данного случая.

— Сколько десятков и сколько отдельных единиц в  первом слагаемом?

Учитель выставляет на наборном полотне 5 десятков палочек и 3 отдельные палочки (или карточки, на которых нарисованы пучки-десятки и отдельные палочки).

— Сколько десятков и сколько отдельных единиц во  втором слагаемом? Будем прибавлять к числу 53 число 34 по частям. Сначала прибавим 3 дес.

Учитель ставит 3 пучка палочек под десятками.

— Сколько ещё надо прибавить?

Учитель добавляет на абак ещё 4 палочки. На языке математики это можно записать так:     

                            53 + 34 = 53 + (30 + 4) = (53 + 30) + 4

           /\

        30  4

— Расскажите по этой записи, как вычислили значе- ние выражения 53 + 34, и назовите результат.

— Кто может сказать, как выполнить это вычисле- ние и записать его короче? (Дети затрудняются с ответом.)

— Какую же учебную цель мы поставим на сегодняш- нем уроке? (Дети сами формулируют цель: научиться делать краткую запись при сложении двузначных чисел.)

Учитель предлагает прочитать уточнённую учебнопознавательную цель, предложенную в учебнике.

После этого один из учеников на доске, а все дети в тетрадях под руководством учителя выполняют записи.

— Запишите первое слагаемое 53. Под ним запишите  число 34 так, чтобы десятки были под десятками, а единицы — под единицами. Слева от чисел, между ними, пишем знак «+». Под числами проведём черту, ниже которой запишем сумму. Такая запись называется записью столбиком. Если числа записываются в столбик, то вычисления начинают выполнять с единиц. Складываем единицы: 3 ед. + 4 ед. = 7 ед. Где запишем цифру 7? (Под единицами.)

Складываем десятки: 5 дес. + 3 дес. = 8 дес. Пишем цифру 8 под десятками. Чему равна сумма? При записи столбиком вычисления выполнять легче. Поэтому если устно трудно найти значение выражения, то его находят письменно.

Таким образом, предлагая специальные задания, учитель показал учащимся недостаточность имеющихся знаний и необходимость их расширения, кроме того, он подвёл учащихся к самостоятельной формулировке учебной задачи, что облегчает учащимся осознание и сохранение этой задачи в течение всего урока.

После этого учитель организует первичное закрепление, в ходе которого ученики проходят этап выполнения действий во внешней речи: дети сначала объясняют по учебнику решение примера 45 + 23, используя иллюстрации и текст на с. 4, а затем с комментированием выполняют задание № 1.

В структуру урока всегда включаются задания на повторение и закрепление наиболее важных вопросов из пройденного материала. Как правило, это повторение ведётся на более высоком уровне обобщения и часто выполняется детьми самостоятельно. На данном уроке продолжается работа по формированию у учащихся умений решать текстовые задачи (№ 2) и устно выполнять сложение и вычитание чисел в пределах 100. При выполнении задания № 2 целесообразно во фронтальной работе составить план решения задачи, а затем предложить ученикам записать её решение в том виде, в каком они сочтут для себя наиболее приемлемым (используя запись решения по действиям или выражением). Что касается задания № 3, то на уроке дети могут выполнить его устно, а дома — письменно.

Очень важно отметить, что на каждом уроке предлагается материал для организации действий учащихся по самоконтролю и самооценке результатов своей учебной деятельности. Этот материал в учебнике, как и в 1 классе, представлен в двух видах: в виде текстов заданий для самоконтроля, данных под красной чертой, или даётся ссылка на пособие «Проверочные работы» с указанием страниц, на которых находятся нужные проверочные работы или предметные тесты.  В методическом плане эта работа во 2 классе может быть организована по-разному: индивидуально — дети самостоятельно выполняют в тетради предложенные задания, а затем учитель организует проверку правильности их выполнения — называет правильные ответы, а ученики ставят знак «+» около правильно выполненных заданий, подсчитывают и записывают число плюсов. Если знак «+» будет поставлен около каждого задания, то это значит, что полученный учеником результат высокий и его можно оценить, нарисовав улыбающегося смайлика. Так же оценивается и результат с одной допущенной ошибкой. Во всех остальных случаях оценкой будет служить рисунок другого смайлика (такие знаки приводятся в пособии «Проверочные работы»). Очень важно помочь ученику понять причину допущенных ошибок и подбодрить тех учащихся, у которых результаты самоконтроля оказались не очень высокими, выразить уверенность в том, что на следующих уроках результаты будут лучше, если ученики учтут допущенные ошибки, осознают, почему они их допустили, и будут стремиться к достижению лучших результатов.

Как видим, форма представления материала для самопроверки и самооценки учащимися полученных ими результатов и методика работы с этим материалом сохраняются, однако во 2 классе меняется сам материал, предназначенный для этих целей, на что следует обратить особое внимание. Так, наряду с проверкой знаний всё чаще осуществляется проверка умений использовать полученные знания при решении различных учебно-познавательных и учебно-практических задач: в предлагаемые материалы уже включаются элементы исследовательской деятельности — сравнение чисел, выражений, способов выполнения задания (ч. 1: с. 11, 13, 16, 17, 26, 31, 35, 47; ч. 2: с. 17, 50, 56), выбор правильного решения (ч. 1: с. 39, 43), выполнение обратных операций (ч. 1: с. 77), выполнение задания несколькими способами (ч. 1: с. 87), составление всех возможных двузначных чисел, используя две (три) заданные цифры (ч. 1: с. 9, 12), а также применение знаний к решению учебно-практических задач (ч. 1: с. 33; ч. 2,

с. 51) и др. Такое содержание материала для самоконтроля способствует формированию умений проводить самооценку не только новых знаний, но и новых  способов учебных действий.

Подводя итог урока, учитель просит детей вспомнить, какую познавательную цель они ставили в начале урока, сравнить учебную цель и полученный результат, высказать своё мнение, достигнута ли эта цель.

Проверку результатов самоконтроля можно организовать в паре: ученики выполняют задания и проверяют работу друг друга.

Задания под красной чертой предназначены только для формирования учебных действий самоконтроля и самооценки, по результатам их выполнения оценки учитель не выставляет.

На полях учебника приводятся разнообразные задания, которые представляют собой дополнительный учебный материал для развития  универсальных учебных действий. Так, задание, предложенное на полях рассмотренной страницы (ч. 2: с. 4), направлено на развитие познавательных универсальных учебных действий: оно требует проведения сравнения и применения знаний в изменённых условиях.

Таким образом, принятая в учебнике структура урока (реализация системно-деятельностного подхода в обучении) способствует  активному участию учащихся в поиске и усвоении новых знаний, в достижении предметных, метапредметных и личностных результатов, соответствующих требованиям ФГОС НОО.

Учебник имеет тематическое построение. В нём разработано 4 темы: «Числа от 1 до 100. Нумерация», «Числа от 1 до 100. Сложение и вычитание» (ч. 1); «Числа от 1 до 100. Сложение и вычитание (письменные вычисления)», «Числа от 1 до 100. Умножение и деление» (ч. 2).

Каждая тема открывается особой страницей (шмуцтитулом), на которой приводится название темы, даётся рисунок или схема, а иногда и рисунок, и схема, на которых отражается математический смысл основных понятий, рассматриваемых в теме, определяются наиболее важные учебнопознавательные цели изучения темы («Узнаем») и планируемые предметные результаты её изучения («Научимся»).

При работе с первым шмуцтитулом (с. 3), по тексту и рисункам которого учащиеся под руководством учителя формулируют учебно-познавательную цель изучения новой темы, составляют план её изучения, учитель обращает внимание детей на то, что, помимо уроков, направленных на решения сформулированных учебных задач этой темы, в неё включены задания повышенной сложности — «Странички для любознательных» (с. 18, 19, 24), материал для обобщения знаний — «Что узнали. Чему научились» (с. 20, 21) и материал для проведения самоконтроля и самооценки результатов изучения темы — «Проверим себя и оценим свои достижения» (с. 22, 23).

Работу со шмуцтитулом рекомендуется включать на каждый первый урок по теме, отводя на это не более 10 мин. Методическая задача учителя при работе со шмуцтитулом заключается в том, чтобы сделать предстоящую работу по освоению основных вопросов новой темы более понятной и осознанной для учащихся, довести до сведения учащихся  цели и перспективный план её изучения, использовать материал шмуцтитула и время, отводимое на ознакомление с ним, для формирования и развития у учащихся универсальных учебных действий, в частности:

•         регулятивных — умений понимать, принимать и сохранять на более длительное время, чем урок, учебную задачу, планировать свои действия;

•         личностных — расширять интерес к изучению нового, укреплять мотивационную основу деятельности ученика;

•         познавательных — умений проводить анализ, соотносить графическую и словесную форму представления учебного материала, выстраивать высказывания и обосновывать их.

Как организовать работу со шмуцтитулом, учитель уже знает, учащиеся тоже знакомы с этим видом учебной деятельности. Однако приобретённый детьми в 1 классе опыт постановки и принятия учебных задач на более длительный, чем один урок, период изучения учебного материала ещё недостаточный.

Во 2 классе, когда дети уже умеют читать, проводить сравнения текста и иллюстрации, повышается уровень их самостоятельности в определении того, что нового они узнают при изучении новой темы, более того, учащиеся самостоятельно пытаются составить варианты плана её изучения (учитель только уточняет последовательность учебных действий). Это помогает развитию коммуникативных учебных действий — вести диалог с учителем и друг с другом, развитию интеллектуальных учебных действий — извлекать информацию из материала, представленного на странице, определённым образом структурировать эту информацию в своём сознании и делать логические выводы.

Рассмотрим, как может быть организована работа, например, по шмуцтитулу, на котором представлена тема «Числа от 1 до 100. Нумерация» (ч. 1, с. 3). Работа по этому шмуцтитулу организуется после того, как будут проведены два урока (ч. 1, с. 4, 5) на повторение, т. е. в начале первого урока (с. 6) по теме, заявленной на шмуцтитуле (с. 3).

Учебно-познавательные цели этого фрагмента урока могут быть сформулированы так:

Предметные: показать учащимся необходимость расширения имеющихся знаний, в частности области чисел, с тем чтобы дети осознали свои затруднения при определении того или иного количества предметов и сделали вывод о необходимости получения новых знаний; формировать умения у учащихся образовывать числа из десятков и отдельных единиц; правильно читать, записывать и сравнивать числа в пределах 100. Метапредметные:

•         регулятивные: настраивать учащихся на формирование умений: понимать, принимать и сохранять учебную задачу, составлять в совместной с учителем деятельности план изучения темы, выполнять учебные действия самоконтроля и самооценки;

•         познавательные: осуществлять поиск нужной информации в учебнике, выполнять операцию сравнения, делать выводы и чётко излагать их;

•         коммуникативные: формировать умение общаться с учителем и одноклассниками, отвечать на вопросы, задавать вопросы.

Личностные: способствовать формированию мотивационной основы учебной деятельности.

Сначала целесообразно вспомнить, какие числа дети узнали в 1 классе, вспомнить, что научились их образовывать, читать, записывать, сравнивать.

— Хватает ли нам этих чисел на уроках, в жизни? (Нет.) Приведите примеры. (При покупках в магазине, при работе над проектом «Числа в загадках, пословицах, поговорках» количество страниц было больше 20, при определении возраста мамы, папы, бабушки и др.)

Учитель предлагает учащимся открыть учебник на нужной странице, рассмотреть её, рассказать, что на ней нарисовано, выяснить, больше или меньше 20 количество мест на рисунке, и сделать вывод, какую же учебную цель надо поставить при изучении новой темы. Далее учитель уточняет и дополняет предложенные детьми формулировки и читает название темы: «Числа от 1 до 100. Нумерация» (если сочтёт необходимым, поясняет смысл термина нумерация (от латинского слова numero — считаю; совокупность приёмов называния и обозначения чисел).

— Что же мы узнаем при изучении новой темы? (Как образуются, читаются и записываются числа от 1 до 100, научимся их сравнивать.)

Учитель обращает внимание на то, что, перечисляя названные действия, ученики  составили план изучения темы, которому и будут следовать.

— Откройте учебник на странице, на которой заканчивается изложение этой темы. Обратите внимание на то, что в конце темы есть рубрика «Проверим себя и оценим свои достижения». Она поможет вам оценить свои результаты по работе над темой, к изучению которой мы приступаем.

Далее целесообразно обратить внимание детей на особенности построения рядов в зрительном зале (по 10 мест в каждом ряду) и перейти к работе по с. 6 учебника.

В содержание каждой темы перед рубрикой «Проверим себя и оценим свои достижения» включена рубрика «Что узнали. Чему научились». Если работа со шмуцтитулом служит для постановки учебно-познавательных целей и планирования предстоящей учебной деятельности, то содержание этих рубрик чаще всего создаёт условия для формирования и развития личностных, познавательных и регулятивных универсальных учебных действий. Рубрика «Что узнали. Чему научились» содержит материал для систематизации и обобщения знаний, для распространения их на более широкую область применения, на выполнение заданий творческого и поискового характера. Работе по материалам этой рубрики учитель по своему усмотрению может посвятить отдельные уроки, цели и содержание которых он определяет заранее, не забывая о необходимости и на этих уроках вести целенаправленное формирование универсальных учебных действий. Так, используя для такого урока материал со с. 20 (ч. 1), учитель может сформулировать его тему и целевые установки следующим образом:

Тема: «Закрепление и систематизация знаний по нумерации чисел от 1 до 100».

Целевые установки

Предметные: закрепить умения образовывать, читать, записывать, сравнивать числа от 1 до 100; закрепить знания о новых единицах длины — миллиметре и метре, соотношениях между изученными единицами длины (1 м = = 10 дм, 1 дм = 10 см,  1 см = 10 мм, 1 м = 100 см), умение сравнивать величины; решать текстовые задачи. Метапредметные:

•         регулятивные: формировать умения понимать, принимать и сохранять учебную задачу и решать её в сотрудничестве с учителем;

•         познавательные: формировать умения ориентироваться в материале учебника и находить нужную информацию (№ 1); объяснять и аргументированно обосновывать выполняемые действия (№ 2);

•         коммуникативные: формировать умения работать в паре (№ 3).

Личностные: способствовать развитию интереса к математике, формированию мотивационной основы учебной деятельности, умений вести поиск решения задач повышенной сложности.

Есть и другой способ использования материала рубрики «Что узнали. Чему научились» — распределить его содержание по урокам темы — 2—3 задания на урок, согласовывая их с целями  и учебным материалом каждого урока.

Материал рубрики «Проверим себя и оценим свои достижения», которым заканчивается изложение темы, как и в 1 классе, представлен в учебнике в форме предметных тестов, что обусловлено тем, что такая форма подачи материала для самоконтроля и самооценки даёт возможность наиболее полно охватить учебные вопросы, изученные в теме. Однако накопленные учащимися в течение первого года обучения математические знания, способы действий и приобретённый ими опыт в проведении самоконтроля и самооценки позволили сделать задания этих тестов более сложными, а ответы к ним менее очевидными, например включить задания, для выполнения которых надо выбрать пропущенное в верном равенстве число или знак арифметического действия, а для проверки того, что ответ выбран верно, выполнить устно не одно, а два-три действия.

Другими словами, сохранённая форма наполняется новым усложнённым содержанием.

Учителю рекомендуется, как и в 1 классе, предложенные тесты размножить на ксероксе по количеству учеников в классе, раздать детям листы с заданиями и перед выполнением первого теста чётко объяснить его структуру, показать, как отмечать выбранный ответ, и рассказать, как зафиксировать ту оценку, которую даст себе каждый из учеников: можно предложить учащимся ту же форму фиксации результата своей работы, которую они использовали при работе в пособии «Проверочные работы», — нарисовать один из трёх смайликов:

 — хорошо (нет ошибок, допущена одна ошибка);

 — средне (без ошибок выполнено не менее половины  заданий); надо повторить те вопросы темы, по 

                                 которым допустил ошибки;

 — плохо (без ошибок выполнено менее половины                                                заданий); надо поработать над вопросами всей                                       темы.

Учитывая, что приобретённые учащимися в 1 классе навыки самооценки результатов своей учебной деятельности находятся на начальном этапе своего формирования, работа по их развитию и совершенствованию во 2 классе проводится под руководством учителя по сценарию, близкому к тому, который использовался в 1 классе, но имеющему некоторые отличия от него. Так, ещё одной из отличительных  характеристик предметных тестов в учебнике для 2 класса (по сравнению с 1 классом) является увеличение количества заданий. Поэтому перед выполнением каждого теста учитель знакомит учащихся с количественными нормами оценки результатов его выполнения. Например, перед выполнением теста «Числа от 1 до 100. Нумерация» (ч. 1, с. 22, 23), который содержит 11 заданий, учитель сообщает, что улыбающийся смайлик ученик может нарисовать, когда он выполнил все задания правильно или допустил только одну ошибку; тот, кто правильно выполнил 6 заданий и более, но допустил две ошибки, рисует спокойный смайлик; тот, кто выполнил верно 5 заданий и меньше, рисует грустный смайлик. (Первый раз рисунки смайликов учитель показывает на доске или на заранее заготовленном плакате.)

Каждый ученик выполняет все задания теста, проверяет их, отмечает правильно выполненные задания знаком «+» и по количеству знаков «+» первоначально оценивает свой результат: рисует своего смайлика. После этого учитель организует проверку: называет верные ответы, а каждый ученик отмечает ранее не обнаруженные им ошибки (если такие будут) и вносит коррективы в свою самооценку — оставляет нарисованного смайлика или рисует другого.

Систематическое проведение такой работы будет способствовать формированию у учащихся умений применять принятые нормы самооценки, более ответственно проводить проверку выполненных действий (находить свои ошибки), анализировать полученные результаты, выявляя неусвоенные разделы темы или способы учебных действий.

Учитель обращает внимание ученика на необходимость дополнительной работы по тем вопросам, в которых были допущены ошибки.

Во 2 классе учащиеся продолжают учиться оценивать результаты своих учебных действий и накапливать опыт в этом виде учебной деятельности, что повышает их мотивацию для дальнейшего, уже более самостоятельного развития и совершенствования своих знаний и учебных действий.

Для более осознанного усвоения учебного материала, для развития слухового восприятия математического текста и формирования коммуникативных универсальных учебных действий в учебнике представлен материал, размещённый в рубрике «Странички для любознательных» и имеющий свой подзаголовок «Помогаем друг другу сделать шаг к успеху» (ч. 2, с. 46, 71).

Этот материал представлен в форме предметного теста вида «Верно? Неверно?», который построен на изученном программном материале. Тест содержит, как правило, не более 12 заданий, среди которых есть как верные, так и неверные высказывания или утверждения.

Данный материал предназначен для организации работы в паре: один ученик читает задание, другой, работающий с ним в паре, определяет, верно это высказывание или нет. Если высказывание верно и ученик это правильно определил, пара переходит к работе над следующим высказыванием; если же ученик определил, что высказывание неверно, то он пытается дать его правильную формулировку, что оценивается вторым участником. После рассмотрения примерно половины заданий теста ученики меняются ролями. В самом названии этого материала отражена его направленность на формирование и развитие у учащихся потребности оказывать друг другу помощь в учебной деятельности, на формирование умений проводить совместное обсуждение математических утверждений, совместно вносить в них исправления, доброжелательно оценивать ответы друг друга.

Работа по таким страничкам проводится после изучения материала той темы, в которую он включён, на одном из уроков закрепления изученного в теме. На такую работу, как правило, отводится 10—15 мин.

Методика работы

над дополнительным материалом учебника

В содержание учебника «Математика. 2 класс» включён дополнительный материал, обеспечивающий формирование личностных, регулятивных, познавательных и коммуникативных универсальных учебных действий. Этот материал позволяет усилить работу по развитию логического мышления, основ компьютерной грамотности, пространственного воображения, речи учащихся, по формированию умений решать задачи практического содержания (задачи-расчёты), работать в паре, помогать друг другу, содержательно общаться и осваивать учебный материал («Поможем друг другу сделать шаг к успеху»). Такой материал размещён в рубрике «Странички для любознательных». Изложим сначала подробно методические подходы к рассмотрению этого материала, который органически включён в общую систему освоения программного материала по математике для 2 класса, а затем рассмотрим методические приёмы работы по содержанию каждой темы курса второго года обучения.

Цели включения в учебник материалов этой рубрики, их содержательная характеристика и классификация были рассмотрены на с. 15—16 настоящего пособия. Основная часть заданий этой рубрики обеспечивает дополнительный материал для развития у второклассников универсальных личностных и познавательных учебных действий, в частности умений решать задачи творческого и поискового характера. Это задания на выявление закономерности следования объектов в заданном ряду, закономерности заполнения свободных окошек (ч. 2: с. 21, № 5; с. 38, № 1; с. 87, № 4, 7).

В 1 классе большое внимание уделялось формированию умений проводить сравнение предметов, групп предметов, чисел, числовых выражений, геометрических фигур, и дети уже имеют некоторый опыт выполнения заданий как на проведение сравнений, так и на выявление закономерности (правила), по которой составлен предложенный в задании ряд, умеют  наблюдать и отмечать (устно описывать) те изменения, которые происходят при переходе от одного объекта к следующему (сравнивать предыдущий и следующий за ним элемент), находить общее в этих изменениях (переходах) и обобщать свои наблюдения, формулировать и использовать найденное правило построения рассматриваемых рядов.

Для продолжения этой работы в учебнике для 2 класса предлагается усложнённый учебный материал, требующий применить знания и изученные способы действий в изменённых условиях. Так, при работе по заданию № 5 (ч. 2, с. 21) ученики используют умения выполнять действия сложение и вычитание чисел, знание зависимости между компонентами и результатом этих действий, умения применять эти знания в изменённых условиях, приобретают опыт поиска решения. Сначала под руководством учителя дети рассматривают образец и устанавливают правило, по которому из чисел, записанных в окошках на стене домика, может быть получено число 11 (8 + 10 – 7 = = 11), а затем, используя найденное правило, вычисляют и называют числа, которые надо записать в свободные окошки каждого домика. При рассмотрении образца очень важно обратить внимание детей на то, что в двух верхних окошках стены записано уменьшаемое, выраженное суммой двух чисел, в нижнем окошке — вычитаемое, а число 11 — разность. Очень полезно при определении чисел в двух первых домиках послушать комментарии учащихся, в которых обязательно должны быть использованы названия компонентов и результата действия вычитание. Комментарии могут быть такими: находим сумму чисел 13 и 18, она равна 31, теперь мы знаем уменьшаемое 31 и разность 11, надо найти вычитаемое; чтобы найти вычитаемое, надо…, или такими: находим сумму чисел 13 и 18, она равна 31, определяем, какое число надо вычесть из 31, чтобы получить 11, это 20. Чтобы найти число для окошка второго домика, надо провести более сложные рассуждения, так как в этом случае неизвестным будет часть уменьшаемого.

— Что известно в этом случае? (Вычитаемое и разность.) Как найти неизвестное уменьшаемое? (Чтобы найти неизвестное уменьшаемое, надо к вычитаемому прибавить разность, в нашем случае: 11 + 12 = 23, уменьшаемое равно 23, следовательно, в окошко надо записать число 16, так как 23 – 7 = 16.) Число для окошка в третьем домике дети находят самостоятельно.

Задание № 1 (ч. 2, с. 38) тоже носит усложнённый характер, так как в построении рядов и столбцов таблицы заложена «чередующаяся» закономерность: в первой строке — плюс 10, плюс 1, а в столбцах — минус 10, минус 1. Для успешного выполнения этого задания учениками целесообразно заданную в учебнике таблицу перенести на доску, затем в ходе фронтальной работы предложить детям определить правило, по которому составлена первая строка, заполнить её числами, тогда у детей будет зрительная опора для выполнения второй части задания: они формулируют правило, по которому должны быть записаны числа в каждом столбце, и выполняют задания, записывая в таблицу нужные числа.

В задании № 4 (ч. 2, с. 87) предлагается из трёх последовательностей чисел выбрать ту, которая составлена по заданному правилу. В ходе выполнения этого задания у детей не только идёт развитие умений наблюдать, сравнивать, определять закономерность построения предложенного ряда чисел, но и отрабатываются навыки устных вычислений. Так, чтобы найти нужную последовательность, ученики устанавливают:

•         первая последовательность составлена по такому правилу: «Каждое следующее число на 3 больше, чем предыдущее», для чего им приходится выполнить по меньшей мере три действия вычитания;

•         вторая последовательность составлена по заданному правилу (для обоснования ответа выполняют действия вычитания);

•         правило, по которому составлена третья последовательность и устно выполняется ряд арифметических действий (сложение или вычитание).

Задание № 7 (ч. 2, с. 87) учащимся предлагается выполнить самостоятельно, так как они уже знакомы с чередующейся закономерностью.

В тему «Числа от 1 до 100. Нумерация» включён материал рубрики «Странички для любознательных» (ч. 1, с. 18, 19). Как уже было сказано, этот материал по усмотрению учителя может быть использован на отдельном уроке или распределён по урокам всей темы. Однако в любом случае следует рассмотреть все задания этой рубрики в ходе изучения темы, так как это дополнительный материал поискового и творческого характера, создающий условия для формирования универсальных, в частности личностных и познавательных, учебных действий. Задания такого вида вызывают большой интерес со стороны учащихся и укрепляют мотивацию изучения математики, а кроме того, знакомят детей с новыми способами поиска решения, развивают способность использовать знания в изменённых условиях. Так, при решении задач № 1—3 (с. 18) учащимся предлагается выполнить решение, «подбирая разные числа и проверяя, подходят ли они для решения задачи». Задачи решаются под руководством учителя.

При решении любых задач очень важно прежде всего добиться того, чтобы все ученики хорошо осознали условие задачи, те взаимосвязи между объектами, о которых в ней говорится. Для этого целесообразно не просто один раз прочитать задачу, а обсудить, о ком говорится в задаче, что говорится в задаче о названных объектах, что надо узнать в задаче. Так, при разборе задачи № 1 (ч. 1, с. 18) целесообразно показать, что подбор чисел для решения не будет произвольным, а сначала будет определяться тем условием, что «больше всего зайцев, их на 5 больше, чем ежей». После того как дети выделят это условие, целесообразно выяснить, какой вывод можно из этого сделать (зайцев не может быть меньше 6, побор чисел для решения начнём с предположения, что было 6 зайцев).

— Проверьте, может ли быть 6 зайцев. (Нет.) Почему?  (Если зайцев 6, то ёж 1, белок 7, а по условию больше всего зайцев, а не белок.)

— Какое число проверим следующим? (Число 7.)

Ученики проводят вычисления, получают ответ: ежей — 2, зайцев — 7, белок — 5 — и убеждаются, что в этом случае все условия задачи выполнены. Важно показать детям, что при таком способе решения надо убедиться в том, что у задачи нет других решений. (Если предположить, что зайцев было 8, тогда ежей — 3 и белок — 3, а по условию задачи меньше всего было ежей.)

Уровень самостоятельности учащихся при решении задачи № 2 (ч. 1, с. 18) может быть более высоким. Прежде всего выясняется, сколько групп зверей участвовало в соревнованиях (2 группы), сколько всего задач они решили (11 задач), как по количеству можно распределить 11 задач между двумя группами (ученики вспоминают состав числа 11 из двух слагаемых: 5 и 6, 4 и 7, 3 и 8, 2 и 9, объясняют, почему не надо рассматривать 1 и 10).

— Какую пару чисел можно исключить сразу? (2 и 9.)  Почему? (Не будет выполнено условие о том, что «все решили разное количество задач».)

— Что известно про количество задач, решённых ежа- ми? (Один ёж решил больше всех, а другой — меньше всех.) Какое предположение можно сделать? (Один ёж решил 1 задачу.)

— Если предположить, что ежи решили 6 задач, а бел- ки — 5, то могло быть, что второй ёж решил… (5 задач), одна белка — … (2 задачи), другая — … (3).

— Проверьте, все ли условия задачи выполняются. (Да.)

— Проверьте, нет ли у задачи других решений. (Дети  рассматривают пару чисел 4 и 7 (ежи — 2 и 5; белки — 1 и 3).) Почему это решение не подходит? (Меньше всех задач решил ёж, а не белка; если предположить, что ежи — 1 и 6, белки — 1 и 3, то видим, что тоже не подходит.)

При решении этой задачи рассуждать можно и так: учитель обращает внимание детей на условие «один из ежей решил меньше всех заданий» и просит сделать выводы из этого условия (один из ежей решил только 1 задание, а белочки могли решить: одна белочка — 2 задания, а другая — 3, так как по условию задачи все участники соревнований решили разное количество заданий, тогда второй ёж мог решить 5 заданий; все эти числа удовлетворяют условию задачи), а затем проверить, не имеет ли задача ещё одно решение (один ёж решил 1 задачу, предположим, что белочки решили 3 и 4 задачи, тогда другой ёж решил 3, что не соответствует условию задачи).

При поиске решения задачи № 3 (ч. 1, с. 19) ученики уже сами должны выделить то условие, опираясь на которое выбирается первое число для проверки: «ежей было на 4 меньше, чем белок», а это значит, что белок было на 4 больше, чем ежей, а следовательно, их не могло быть меньше 5. Если белок 5, ежей 1, то зайцев 4, т. е. ежей на 3 меньше, чем зайцев.

— Нашли одно решение задачи. Проверьте, нет ли дру- гих решений. (Если предположить, что белок было 6, тогда ежей — 2 и зайцев — 2, а по условию задачи ежей было на 3 меньше, чем зайцев.)

После чтения задачи № 4 (ч. 2, с. 21) дети повторяют её условие и вопрос, выполняют схематический чертёж. Учитель объясняет, что эту задачу следует решать подбором чисел, а числа записывать в таблице: в первой строке число пирожков с грибами, во второй — с капустой и в третьей — с яблоками. Запись на доске:

Предположим, что с грибами был 1 пирожок. Запишем это числ о в первой строке. Сколько тогда будет пирожков с капустой? (4.) Запишем это число во второй строке. Сколько тогда будет пирожков с яблоками? (9.) Как узнали? (С грибами и капустой вместе было 5 пирожков, а всего было 14. 14 – 5 = 9.) Запиш ем это. Подходят ли эти числа по условию задачи? (Нет. Пи рожков с грибами должно быть больше, чем с яблоками, а здесь меньше.)

Теперь предположим, что с грибами было 2 пирожка. Запишем 2 в первой строке. Сколько тогда будет пирожков с капус той и сколько с яблоками? Запишем эти числа в таблице. Выя сняется, что и эти числа не подходят, так как с яблоками пирожков получилось больше, чем с грибами.

Учитель предлагает детям самостоятельно продолжить заполн ение таблицы, полагая, что с грибами было сначала 3 пирожка, а затем 4. Сравнивая в каждом случае полученные числа, дети находят ответ на вопрос задачи: с грибами было 4 пирожка, а с яблоками — 3 пирожка (если продолжить заполнение таблицы, то получится ещё одно решение). 

При организации парной работы в игре «Кто первым наберёт 10» целесообразно сначала убедиться в том, что все хорошо усвоили условия игры, и предложить детям 2—3 раза сыграть с соседом по парте. Вполне возможно, что дети не смогут найти план успешной игры. Можно предложить им провести анализ хода игры «от конца» (ещё один новый для детей способ действия):

— Если ты хочешь первым назвать 10, то какое чис- ло ты должен назвать первым перед десятью? (Число 7.) Объясни почему.

— Но для того чтобы первым назвать 7, какое число  ты должен назвать первым перед числом 7?

— В к аком случае начинающему игру всегда обеспечен успех?

— Как надо стремиться играть в других случаях?

При решении задач на построение цепочки логических рассуждений (ч. 1: с. 36, № 2; с. 51, № 2; ч. 2: с. 20, № 2; с. 39, № 4; с. 86, № 1) следует обратить внимание детей, можно ли сделать вывод и какой, исходя из условий задачи, и что даёт этот вывод для продолжения решения.

При решении задачи № 2 (ч. 1, с. 36) вспомогательные вопросы могут быть, например, такими:

— Станет ли у обезьянок орехов поровну, если у боль- шой обезьяны взять 6 орехов и не отдавать их маленькой? (Да, станет.)

— Как разделить 6 орехов между двумя обезьянами  так, чтобы орехов у них оставалось поровну?

— Дайте ответ на вопрос задачи.

Дополнительно можно, изменив вопрос задачи, спросить:

— Сколько орехов большая обезьяна отдала маленькой,  если у маленькой стало на 4 ореха больше, чем у большой обезьяны?

Внимательное чтение условия задачи № 2 (ч. 1, с. 51) позволяет сделать вывод, что у Севы — собачка, а использование этого вывода даёт возможность определить, что у Вани — кораблик (так как у него не лиса и не собачка), значит, у Димы — лиса.

При решении задачи № 2 (ч. 2, с. 20) дети проводят рассуждения с опорой на рисунок, сравнивая количество больших и маленьких рыбок в каждом ведёрке и сопоставляя это с условием задачи, а при решении задачи № 4 (ч. 2, с. 39) целесообразно выполнить схематический чертёж по условию задачи:

                     Ёж                      

Белка

Заяц

и сделать вывод.

В задании № 1 (ч. 2, с. 86) учащимся предлагается делать вывод, основываясь на том, что под рисунками даны все неверные записи. После чтения задачи учитель спрашивает:

— Какой вывод можно сделать из записей под первым  и вторым поросёнком? (Первым нарисован Нуф.)

— Закончите рассуждения. (Вторым нарисован Ниф,  третьим — Наф.)

В задачах № 3 (ч. 2, с. 21) и № 2 (ч. 2, с. 86) применяются знания состава чисел из двух слагаемых, а в задаче № 4 (ч. 2, с. 65) — знания и зависимости между компонентами и результатом действия сложение.

Для получения устойчивых метапредметных результатов у учащихся на «Страничках для любознательных» предлагаются дополнительные задания, в которых требуется применить знания в изменённых условиях (ч. 1: с. 36, № 1; с. 50, № 1; с. 70, № 1; ч. 2: с. 21, № 3; с. 65, № 4). Общий методический приём при поиске решений в таких случаях — это, во-первых, повторение и активизация тех знаний и способов действий, на которых будет выстраиваться решение и которые уже усвоены детьми, и, во-вторых, выявление в заданном объекте (рисунке, схеме, числовом выражении и др.) того, что о нём непосредственно не дано, что будет получено в ходе решения. Это достигается с помощью специально поставленных учителем  вопросов, которые помогут вспомнить нужные приёмы, зависимости, свойства действий и направить размышления детей в нужное русло.

Во 2 классе в рубрику «Странички для любознательных» введены задачи-расчёты, задачи практического содержания (ч. 1: с. 24, № 1—4), при решении которых учащиеся будут сравнивать величины, учиться читать и заполнять предложенные таблицы, используя условие задачи.

В учебнике усилена база для развития пространственного воображения учащихся. На «Страничках для любознательных» предлагаются задания на дополнение начерченных фигур до фигур заданного вида (ч. 1: с. 51, № 3) и на составление фигуры заданного вида из предложенных частей (ч. 2: с. 39, № 3). Задания такого вида выполняются графическим способом в первом случае и практическим способом во втором.

На «Страничках для любознательных» размещены также задания, которые продолжают начатую в 1 классе линию на формирование и развитие алгоритмического мышления у младших школьников, что создаёт базу для последующего овладения ими основами компьютерной грамотности. Это задания, которые продолжают линию, начатую в 1 классе: задания, связанные с вычерчиванием заданных фигур и узоров (ч. 1: с. 37, № 5; ч. 2: с. 28, № 3), направленные на формирование и развитие умений действовать по плану, составлять план  действий для выполнения задания, проводить поэтапный контроль за выполнением плана действий.

Основная методическая задача учителя — отслеживать точность графического следования плану и правильный порядок действий при составлении плана по предложенному узору.

В учебнике получает продолжение и развитие весьма полезный для формирования основ алгоритмического мышления приём использования идеи условной Вычислительной машины, работающей как оператор по выполнению арифметических действий сложение, вычитание и умножение. Это задания на «Страничках для любознательных» (ч. 1: с. 19, № 5; с. 51, № 4; ч. 2: с. 28, № 2; с. 39, № 5; с. 87, № 6). Приведём в качестве примера одно из заданий (ч. 2: с. 28, № 2), которое поможет раскрыть не только содержательную, но и методическую сторону работы над этим заданием.

Напомним, что под алгоритмом, как правило, понимают общепонятное и точное предписание, какие действия и в каком порядке необходимо выполнить для решения любой задачи из данного вида однотипных задач.

Это не строгое определение, а лишь разъяснение того, что обычно вкладывается в понятие алгоритма. В задании № 2 (ч. 2, с. 28) приводится изображение Вычислительной машины, которая выполняет два действия ( + 8 – 3). Работа проходит под руководством учителя. Ученики сначала дополняют план работы предложенной машины, а затем отвечают на вопрос: «Какое число будет получаться на выходе, если в машину ввести число: 23; 48; 19; 56; 64; 77?» Эта часть задания, как правило, затруднений у детей не вызывает. Большая часть ошибок приходится на ту часть задания, в которой задаются числа, полученные на выходе из машины, если в неё были введены заданные числа (30; 43; 17; 26), так как в этом случае применяются действия, обратные заданным при описании машины. Вспомогательные вопросы учителя в случаях затруднений могут быть, например, такими:

— На выходе получили число 30. В результате како- го действия его получили? (Из некоторого числа вычли 3 и получили 30.) Из какого числа вычли 3, если получили 30? (Из 33.)

— Как получили число 33? (К некоторому числу при- бавили 8 и получили 33.)

— К какому числу надо прибавить 8, чтобы получить 33?  Или: сумма 33, одно слагаемое 8. Чему равно другое слагаемое? (25.) Сделайте вывод. (На вход было подано число 25.)

Далее учащиеся определяют числа, поданные на вход в машину, самостоятельно, учитель следит за тем, чтобы не было ошибок. В достаточно подготовленном классе в конце выполнения этого задания можно предложить детям составить план, по которому они будут определять число, поданное в описанную машину, по числу, полученному на выходе из неё. (К числу, полученному на выходе, прибавляем 3 и из результата вычитаем 8.)

После введения новых для учащихся арифметических действий расширяется круг действий, выполняемых Вычислительной машиной. Так, во втором полугодии предлагается задание (ч. 2: с. 87, № 6), в котором Вычислительная машина умножает на 2 поданное в неё число.

Выполнение этих заданий можно провести, организовывая работу в паре: один участник называет число на входе в машину, другой — на выходе из неё, после использования 2—3 чисел ученики меняются ролями.

Эта линия имеет продолжение и развитие в учебниках для следующих классов, что создаёт условия для раннего введения в обучение простейших идей информатики, способствует формированию у учащихся алгоритмического стиля мышления (умений планировать свои действия и строго следовать намеченному плану, проводя контроль на каждом этапе его выполнения).

Ещё одна серия заданий — это задания, которые предлагают работу с логическими высказываниями вида «Все», «Каждый», «Если…, то…» и др. «Логическое высказывание» — это упрощение термина «суждение» (ч. 1: с. 71, № 3; ч. 2: с. 28, № 1; с. 65, № 5; с. 86, № 3). Высказывание — это утверждение, которому всегда можно поставить в соответствие одно из двух логических значений: «ложь» (неверно) или «истина» (верно). Например, «Москва — столица Российской Федерации» — высказывание, а предложение «В городе идёт снег» высказыванием не является.

Выполнение таких заданий будет способствовать формированию основ компьютерной грамотности у детей, так как, во-первых, в цифровой, в том числе и в компьютерной, технике используется двоичная система счисления (1 — да; 0 — нет), а во-вторых, при составлении программ для компьютера часто используются разные продолжения программы: если высказывание верно, программа будет иметь одно продолжение; если высказывание неверно, продолжение программы будет другим.

Среди заданий этого вида в учебнике есть такие, которые построены на геометрическом материале и в которых учащимся предлагается не только определить, какое из приведённых высказываний верно для заданного рисунка, но и дополнить начатое высказывание так, чтобы оно было верным для рассматриваемого рисунка. Работа проводится фронтально под руководством учителя: дети читают по одному высказыванию и дают ему свою оценку: «верно» или «неверно», обосновывая её.

В рубрику «Странички для любознательных» включён материал «Готовимся к олимпиаде», задания конкурса «Смекалка» (ч. 2, с. 95). Цель включения этого материала состоит в том, чтобы сориентировать учителя на такой вид внеурочной деятельности, как подготовка второкласс- ников к школьной олимпиаде, и задать уровень сложности предлагаемых для этого заданий. В ходе организации внеурочной работы количество таких заданий может быть увеличено как за счёт использования пособия «Для тех, кто любит математику. 2 класс» авторов М. И. Моро, С. И. Волковой, так и за счёт творческой инициативы учителя, который сам подбирает задания заданного уровня сложности. Этот материал по своему содержанию не выходит за рамки программного материала второго года обучения, но и не дублирует материал учебника, чаще всего задания носят нестандартный характер и требуют от учащихся смекалки, умений проводить логические рассуждения и делать выводы. Олимпиада в начальный период обучения занимает важное место в развитии детей, повышает интерес к предмету, служит развитию творческого желания, однако учителю важно поддержать любознательность детей и в период подготовки к олимпиаде разумно дозировать нагрузки как в качественном, так и в количественном отношении.

Опыт организации такой работы показывает, что для учащихся 2 класса целесообразно на одном занятии (25— 30 мин) предлагать не более четырёх заданий заданного в учебнике уровня сложности.

Для усиления деятельностного метода в обучении, формирования у учащихся умений работать с информацией и создания условий для наиболее эффективного перехода во внеурочную деятельность в учебники математики (авторского коллектива М. И. Моро и др.) включена новая для начальной школы рубрика «Наши проекты», в учебнике для 2 класса это два проекта по темам «Математика вокруг нас»: «Узоры и орнаменты на посуде» (ч. 1, с. 48, 49) и «Оригами» (ч. 2, с. 36, 37), по одному в каждой из двух частей.

Участие школьников в разработке проектов обеспечивает и предполагает развитие познавательных интересов детей, умений проводить исследования и ориентироваться в информационном пространстве, проводить поиск и сбор информации, анализировать и систематизировать собранную информацию, использовать приобретённые знания для решения новых теоретических, практических и прикладных задач, способствует расширению кругозора учеников. В ходе работы над проектами у учащихся формируются и развиваются коммуникативные универсальные учебные действия: дети учатся сотрудничать друг с другом, работать парами и в разных по количеству участников группах, выполнять различные роли: собирать информацию, оценивать собранный материал, представлять его в виде текста, выполнять рисунки к текстам и схемам, составлять математические тексты к рисункам и др. Очень важно также, что в процессе такой работы у учащихся формируются основы информационной и компьютерной грамотности.

Участвуя в проектной деятельности в 1 классе, учащиеся получили самые начальные представления о том, что такое «Наш проект», что при работе над проектом необходимо осознать (принять) цель его создания и решать те задачи, которые приведут к его успешному завершению (получению результата), т. е. наметить план работы над проектом. Дети сумели осознать, что выполнение намеченного плана требует, во-первых, поиска дополнительной информации из разных источников, а во-вторых, объединённых усилий группы учащихся, так как объём предполагаемой работы достаточно велик.

При работе в группах у детей формировались основы коммуникативных умений: согласовывать свои действия и помогать друг другу, обсуждать возникающие затруднения, высказывать свои суждения и принимать суждения других. Кроме того, дети получили представления о том, что о проделанной ими работе можно рассказать другим людям, показать результаты своего труда, что, безусловно, способствует формированию у детей позитивной самооценки.

При работе над проектами во 2 классе учителю следует обратить внимание на то, чтобы перечисленные представления детей постепенно переходили в умения, чтобы возрастал уровень их активности и самостоятельности на всех этапах работы над проектом, развивались умения контролировать свои действия и действия учеников, работающих в одной с ними группе. Во 2 классе дети могут не только предложить свой вариант плана работы над проектом, но и отслеживать его выполнение, соблюдать и контролировать временную протяжённость его этапов. Во 2 классе следует подключать задачи творческого характера и формировать у детей умения их решать. Большое внимание необходимо обратить на формирование коммуникативных умений, в частности умения сотрудничать с другими детьми: чётко высказывать своё мнение, выслушивать мнение других детей, обсуждать различные мнения и вырабатывать единое решение, вежливо и доброжелательно общаться друг с другом.

Рассмотрим один из возможных способов организации работы (подготовительный этап) по проекту «Оригами»

(ч. 2, с. 36, 37).

Целевые установки (для всего проекта)

Предметные: вспомнить особенности такой геометрической фигуры, как квадрат, практическим способом исследовать особенности квадрата, закрепить умения делить квадраты на разные фигуры (квадраты меньших размеров, треугольники и др.).

Метапредметные:

•                     регулятивные: понимать, принимать и сохранять поставленную познавательную задачу; планировать свои действия в соответствии с поставленной целью; оценивать результаты проекта;

•                     коммуникативные: умения работать в группе: координировать свои действия с действиями товарищей по совместной работе, вести диалог, обсуждать возникающие вопросы, прислушиваться к мнению товарищей, формулировать собственное мнение, аргументированно отстаивать его, принимать совместное решение; принимать участие в обсуждении проекта;

•                     познавательные: использовать знаково-символические средства, в том числе чертежи и схемы для выполнения задания (конструирование изделий в стиле оригами); осуществлять поиск необходимой информации с использованием под руководством взрослых различных источников, в том числе доступного пространства Интернета, анализировать и систематизировать собранную информацию; строить речевые высказывания с использованием математических терминов.

Личностные: развивать интерес к новым знаниям, к способам действий, к учебному предмету «Математика», усиливать мотивационную сторону обучения, формировать способность к оценке выполненной работы, показывать связь математики с жизнью и искусством.

Работу над проектом целесообразно начать на уроке закрепления (ч. 2, с. 40) после того, как будет проведено несколько уроков по изучению геометрической фигуры квадрат. На обсуждение проекта и предстоящей проектной деятельности учащихся выделяется на этом этапе не более 15 мин. Учитель называет тему и обсуждает с учащимися, почему именно сейчас предлагается  эта тема, готовы ли они к её выполнению, обсуждает порядок работы по названной теме, возможные источники информации (энциклопедии, различные книги, беседы со взрослыми, доступная сеть Интернет, воспользоваться которой ребёнок сможет с помощью взрослых), способы сбора информации и её представления, рассматриваются возможные этапы работы над темой, разделение учащихся на группы для работы по разным направлениям, определяются задачи каждой группы в предстоящей работе, а также тот результат, который дети должны получить по завершении работы над проектом, например организовать выставку изготовленных ими изделий. Однако основная работа переносится во внеурочную деятельность. Для этого учитель просит детей заготовить прямоугольники (квадраты), вырезанные из бумаги разного цвета и разного размера. На начальном этапе проводятся упражнения по отработке основных элементов складывания, которыми должны овладеть дети, при этом работа проводится под руководством учителя, но учитель выслушивает и предложения детей (дети рассказывают, как это сделать):

•                     преобразовать прямоугольник в квадрат;

•                     сложить прямоугольник или квадрат пополам;

•                     сложить квадрат так, чтобы найти центр квадрата

(рассмотреть два способа);

•                     загнуть сторону квадрата (край листа) к середине;

•                     сложить квадрат в 2 треугольника (сложить квадрат по диагонали);

•                     загнуть 2 угла квадрата к середине, так получается

«Воздушный змей» (можно дать рисунки);

•                     загнуть все углы квадрата к центру («Конверт»).

Заготовка должна иметь точную прямоугольную (квадратную) форму, линии сгиба изделия должны тщательно проглаживаться. Совмещение углов и сторон в процессе складывания должно быть точным.

Конструирование из бумаги — процесс не из простых, но удивительно интересный для ребёнка, так как из листа бумаги — плоской фигуры — он создаёт объёмное изделие.

Деление класса на группы можно провести по видам изготавливаемых поделок: животные, птицы, цветы, игрушки и другие объекты.

Конструирование из бумаги представляет для учащихся начальной школы некоторые трудности, так как у них ещё слабо развита координация мелкой мускулатуры и недостаточно развит глазомер. Чтобы вызвать у детей интерес к изготовлению изделий в стиле оригами и эмоционально настроить их на эту деятельность, целесообразно показать несколько готовых изделий, некоторые из них дети, возможно, захотят изготовить, или показать процесс изготовления одного из изделий. Мы предлагаем разбить класс на несколько небольших групп (3—4 человека), для каждой группы выбрать сначала одно для всех участников группы изделие, но изготовить его из квадратов разных размеров и разного цвета.

В ходе работы участники каждой группы составляют план действий по изготовлению выбранного изделия, помогают друг другу в его изготовлении, обсуждают изготовленные изделия, могут придумать небольшой сказочный рассказ, как квадрат превратился в бабочку (рыбку, кораблик и др.).

Предлагаемые для изготовления изделия не должны быть очень сложными. Мы рекомендуем на первом этапе (после овладения учащимися базовыми приёмами складывания) изготовить изделия: «Бабочка», «Рыбка», «Лягушка», «Самолётик»; на втором этапе: «Заяц», «Птица-синица», «Сова», «Воздушный змей», «Солонка», «Пароход» и др., по выбору учителя и учащихся. Инструкции по изготовлению этих изделий учитель сможет найти в Интернете, достаточно набрать в поисковом окне слово «оригами».

Очень важно намеченный проект довести до успешного завершения и оставить у каждого ребёнка ощущение радости от освоения новых способов действий, гордости за выполненную работу и полученный результат. Будет очень хорошо, если учитель сумеет заинтересовать детей возможностью дальнейшего творческого использования изготовленных изделий: можно придумать сказку, как «оживал» квадрат и «превращался» в бабочку, в рыбку, в лягушку; можно написать небольшой сценарий и поставить маленький спектакль по мотивам какой-либо сказки, например «Заяц и Лиса», изготовив действующих лиц в технике оригами, а домики из картона, или аналогичным образом подготовить инсценировку сказки «Лиса и Журавль», или выполнить то, что предложат сами дети. Всё это будет хорошим дополнением к выставке изделий, подготовленной для презентации. Не менее интересным будет и проведение конкурса на лучшее изделие в каждой группе, когда в качестве приза будет выбрано какое-нибудь очень сложное изделие, выполненное в технике оригами учащимися старших классов.

После завершения работы над проектом учащимся предоставляется возможность обсудить ход и результаты своей работы (что получилось, что не удалось сделать и почему или что нужно было сделать иначе), а затем провести презентацию результатов своей работы, рассказывая о ней другим детям, ученикам другого класса, родителям. Важно, чтобы в процессе такого представления дети услышали одобрение и похвалу в свой адрес.

Описание процесса работы над этим проектом даёт возможность выделить основные этапы его выполнения:

1)       знакомство с темой, мотивацией её выбора, постановка той познавательной задачи, которую предстоит исследовать, тех новых знаний и способов практических действий, которыми надо овладеть в процессе работы; определение планируемых результатов и способа их представления;

2)       организация деятельности учащихся для решения поставленных задач (организация групп, разделение обязанностей между членами образовавшихся групп, выбор координатора работ в группе и др.);

3)       определение источников информации, рассмотрение специфики информации, способов обработки и особенностей представления найденной и отобранной информации;

4)       планирование работы, определение промежуточных контрольных этапов её выполнения и даты завершения работы над проектом, даты презентации результатов проделанной работы;

5)       обсуждение критериев оценки (соответствие итогов работы поставленным целям, своевременное выполнение заданий на отдельных этапах, аккуратность оформления, полнота собранной информации и др.);

6)       поиск и определение возможностей творческого использования полученных результатов, постановка новых задач на базе достигнутых результатов;

7)       анализ полученных результатов, оценка процесса и результатов проектной деятельности учителем и самими детьми, представление конечного продукта, выводы для теоретического и практического использования при работе над последующими проектами.

В начальной школе проектная деятельность является одним из компонентов формирования личностных, регулятивных, познавательных и коммуникативных универсальных учебных действий, закладывает основы проектных умений, подготавливает детей к успешному выполнению более сложных проектов в 5—11 классах. Оценка за проект не выставляется и никак не влияет на итоговые оценки: в этой работе очень важен процесс работы над проектом, осмысление поставленных задач, составление плана их решения, поэтапное выполнение намеченного плана, общение друг с другом в процессе работы и др. Большая работа выпадает на долю учителя: ему предстоит руководить работой на протяжении всей деятельности учащихся, контролировать ход проектной деятельности, помогать детям советом и делом как в ходе работы над проектом, так и при подготовке презентации.

Как показывает практика, уже в младшем школьном возрасте дети активно включаются в общие дела, в ходе выполнения которых возникает настоящее сотрудничество: дети помогают друг другу, осуществляют взаимный контроль, у них формируются навыки конструктивного общения со сверстниками, желание помогать друг другу, развиваются отношения уважения друг к другу, формируются общие интересы и дружеские отношения. При проведении регулярной работы над проектами у учащихся формируются основные метапредметные умения, соответствующие требованиям ФГОС НОО, и закладываются основы для достижения большинства личностных результатов.

Методика работы

по основным вопросам предметного содержания

Теперь перейдём к более подробному  рассмотрению методики работы по основным темам курса второго  года обучения (по полугодиям), включая рекомендации как по освоению предметных знаний, так и по формированию универсальных учебных действий.

ПЕРВОЕ ПОЛУГОДИЕ

ЧИСЛА ОТ 1 ДО 100

В первом полугодии выделяют 2 основные темы:

Нумерация (16 ч)

Сложение и вычитание (48 ч)

Основное содержание работы в первом полугодии составляю т нумерация двузначных чисел и устные приёмы сложения и вычитания в пределах 100. Параллельно изучаются вопросы, отн осящиеся: к измерению величин (длины, стоимости, времени); к алгебраической пропедевтике (числовые выражения, чис ловые равенства и неравенства, буквенные выражения, уравнен ия); к геометрической составляющей курса (длина ломаной

ли нии, периметр многоугольника).

Продолжается обучение решению задач: рассматриваются нов ые виды простых и составных задач; вводится понятие задачи, обратной данной; используются различные способы моделирования задачи (схематический рисунок, краткая запись, чертёж); вводится запись решения составной задачи выражением; учащиеся знакомятся с разными способами решения задач.

Как видно даже из перечня вопросов, материал первого по лугодия разнообразный, но несложный. Практически вся первая четверть (8—9 недель), когда рассматривается нумерация чисел в пределах 100 и проводятся первые уроки по теме «Сложение и вычитание», по существу, является подготовкой к изучению устных приёмов вычислений с двузначными числами. За это врем я необходимо повторить материал, изученный в 1 классе, удел ив особое внимание табличным случаям сложения и вычитания.

Однако не следует с первых дней требовать заучивания таблиц наизусть. Полезнее поработать над приёмами вычислений: решать примеры с подробными, а потом с краткими пояснениями вслух, затем с пояснениями про себя, постепенно ускоряя темп рабо ты.

Напомним, что действия с двузначными числами с помо щью как устных, так и письменных приёмов вычислений также закрепляют знание табличных случаев сложения и вычитания, поэтому при постоянной работе в течение всего года дети, без условно, усвоят таблицы, что является одним из основных требований программы 2 класса по математике.

Перейдём к рассмотрению конкретных тем первого полугодия.

ЧИСЛА ОТ 1 ДО 100

Нумерация

В итоге работы над темой дети овладеют след ующими знаниями, умениями, навыками:

•         научатся образовывать числа из десятков и отдельных еди ниц и правильно называть числа в пределах 100;

•         научатся выделять в числе десятки и отдельные единицы и правильно его записывать;

•         узнают порядок следования чисел при счёте и научатся прак тически выполнять счёт предметов по одному и используя груп пировку предметов в десятки;

•         научатся сравнивать числа, используя разные знания по нум ерации: 34 меньше, чем 35, так как при счёте 34 называют раньше, чем 35; 49 меньше, чем 94, так как

4 десятка меньше, чем 9 десятков;

•         научатся складывать и вычитать числа на основе знания: 1) натуральной последовательности: 89 + 1, 90 – 1; 2) десятичног о состава чисел: 20 + 5, 25 – 5, 25 – 20; научатся заменять чис ло, содержащее десятки и единицы, суммой по образцу: 78 = 70 + 8 (понятие разряда и разрядных слагаемых вводится в 3 классе);

•         познакомятся с конкретными представлениями о новых единицах длин ы — миллиметре и метре, усвоят соотношения между изуч енными единицами (1 м = 10 дм, 1 дм = = 10 см, 1 см = 10 мм, 1 м = 100 см), научатся находить длину предметов с помощью как одной, так и двух единиц длины, а также заменять одни еди ницы другими;

•         узнают, что в 1 р. содержится 100 к., научатся набирать 1 р. одинаковыми и разными монетами.

Как уже отмечалось, в процессе изучения этой темы повтор яется материал 1 класса: отрабатываются навыки табличного сложения и соответствующих случаев вычитания, закрепляются умения решать простые и составные задачи, выполняются упраж нения с геометрическими фигурами (отрезком, ломаной, много угольником).

По учебнику на изучение нумерации отводится 16 уроков (см.: «Тематическое планирование», с. 140), однако в за висимости от особенностей конкретного класса учитель может несколько изменить время работы над данной темой.

Наглядные пособия и дидактический материал

Демонстрационные пособия

1)       Пучки — десятки палочек и отдельные палочки для де монстрации образования и десятичного состава двузначных чисел. С этой же целью можно использовать полоски с кружками или треугольниками для иллюстрации десятков (10 полосок по 10 фигур) и единиц (полоски с 1, 2, ..., 9 фигурами). Иногда вместо полосок используют карточк и-прямоугольники с изображением числовых фигур (точ ек) для иллюстрации единиц и карточки-треугольники, изоб ражающие десятки (пособие предложено автором Л. Г. Петерсон).

2)       Абак — таблица с двумя рядами карманов и надписями «Десятки», «Единицы» (рис. на с. 8 учебника) для иллюс трации позиционного принципа записи двузначных чисел.

3)       Модель метра, на которой выделены дециметры и сант иметры, для иллюстрации отдельных чисел (например, 32 см — это 3 дм и ещё 2 см) и натур ального ряда чисел.

4)       Карточки с цифрами 0, 1, 2, ..., 9 и числами 10, 20, 30, ... , 90 для образования двузначных чисел и замены дву значных чисел суммой разрядных слагаемых.

Индивидуальные пособия

1)       Пособие, с помощью которого учащиеся могут иллюстрир овать образование и десятичный состав двузначных чисел (пучки палочек и отдельные палочки или их рисунки).

2)       Карточки с цифрами 1, 2, ..., 9 и числами 10,

20, ..., 90.

3)       Модель метра с выделением дециметров и сантиметров, изготовленная самими учащимися.

На первом уроке при ознакомлении детей с учебником выяс няют, что можно узнать по обложке, титульному листу, оглавлен ию. Подробно рассматривается шмуцтитул (с. 3), по тексту и рисункам которого учащиеся под руководством учителя формулируют учебно-познавательную цель изучения новой темы, составляют план её изучения. Учитель обращает внимание детей на то, что, помимо уроков, направленных на решения сформулированных учебных задач этой темы, в неё включены более сложные задания — «Странички для любознательных» (с. 18, 19, 24), материал для обобщения знаний — «Что узнали. Чему научились» (с. 20, 21) и материал для проведения самоконтроля и самооценки результатов изучения темы — «Проверим себя и оценим свои достижения» (с. 22, 23). Более подробное изложение методических подходов к этой работе дано в настоящем пособии на с. 26. Дети, как правило, проявляю т большой интерес к новым числам, однако на первых уроках в учебнике рекомендуется повторить основные вопросы нумерации на изученном материале.

Упорядочивая числа (с. 4, № 1, с. 5, № 1), дети читают их, сравнивают («Какое число самое маленькое? Какое самое боль шое?»), объясняют десятичный состав отдельных чисел («Скольк о десятков и отдельных единиц в числе 15? в числе 19?»), вспо минают правила записи двузначных чисел, объясняя, на каком месте, считая справа налево, записывают единицы, а на каком — десятки. Здесь же отрабатывается знание порядка следования чисел при счёте («Какое число называют при счёте перед чис лом 3? числом 13? числом 23? Какое число называют при счё те после числа 6? числа 16? числа 36?» и т. п.).

Следующим этапом на этих уроках может стать работа над формированием вычислительных навыков. С этой целью полезно выполнить устные вычисления (с. 4, № 2; с. 5, № 2) или письменное решение примеров (с. 4, № 7;

с. 5, № 3, 4) с объяснением приёмов вычислений. Например, при решении примера 8 – 4 можно вычесть число 4 по частям (8 – 2 – 2), а можно вспомнить состав числа 8 и правило: «Если из сум мы вычесть одно слагаемое, то получится другое слагаемое» (8 = 4 + 4, 8 – 4 = 4). Другой пример: 2 + 6 — прибавлять числ о 6 по частям неудобно, применим приём перестановки слага емых, а в примере 6 + 2, если забыт результат, можно приба вить по частям число 2 (6 + 1 + 1 = 8).

Так как многие дети испытывают затруднения в записи цифр и в расположении записей в тетради, то для предупреждения ошибок и отрицательных эмоций надо не только отрабатывать приёмы вычислений, но и давать образцы выполнения задан ий на доске. В школьной практике есть опыт, когда на первом — третьем уроках все задания дети выполняют на листочк ах, для того чтобы впоследствии не расстраиваться, глядя на плохо оформленную первую страницу тетради.

Для закрепления вычислительных навыков целесо-образно исп ользовать также занимательные упражнения и игры. Некоторые из них даны в учебнике на полях или под заголовком «Задания на смекалку». Так, уже на полях с. 4 есть задание на классифи кацию «Разбей примеры на две группы». Важно, чтобы, после того как все примеры будут прочитаны и решены (можно запи сать их на доске), дети назвали разные варианты решения, т. е. нашли разные основания классификации (по числам, действ иям, ответам). Здесь полезно выделить две группы связан ных между собой примеров:

1) 6 + 3, 3 + 6, 9 – 3, 9 – 6; 2) 2 + 8, 8 + 2, 10 – 2, 10 – 8.

Выписывая вместе с детьми первую группу примеров, можно повторить названия чисел при сложении, переместительное свойс тво и связь между суммой и слагаемыми. Затем предложить по аналогии выписать и решить самостоятельно вторую группу при меров.

Как видим, это задание наряду с закреплением вычислительн ых навыков учит детей наблюдать, сравнивать, обобщать, обос новывать свои действия, т. е. носит чётко выраженный характер по развитию познавательных универсальных учебных действий.

На самом уроке упражнения, направленные на формирование вычислительных навыков (устное и письменное решение примеров, игры, занимательные упражнения), по усмотрению учителя могут быть даны одним блоком или по отдельности, перемежаясь с другим учебным материалом (задачами, геометрическими заданиями и т. п.).

Приступая к решению задач (с. 4, № 4), надо вспомнить, что в каждой задаче есть условие и вопрос; в условии записывают то, что известно, а в вопросе — то, что надо узнать. Обычно первую задачу на нахождение суммы дети решают легко. К раб оте над ней можно привлечь Памятку, которая помогает формировать регулятивные УУД (общий план действий при решении любой задачи):

1.    Читаем задачу.

2.    Называем условие (что известно).

3.    Называем вопрос (что надо узнать).

4.    Объясняем.

5.    Решаем.

6.    Называем ответ.

При составлении второй задачи (на разностное сравнение) следуе т обратить внимание детей на то, что изменить нужно только воп рос, условие задачи остаётся прежним. Объясняя решение («По чему для ответа на вопрос надо из 10 вычесть 6?»), следует вспом нить правило: «Чтобы узнать, на сколько одно число больше или меньше другого, надо из большего числа вычесть меньшее».

Задача № 5 (с. 4) с двумя вопросами и, следовательно, с дву мя ответами. После записи её решения по действиям полезно выяснить, можно ли ответить на второй вопрос, не ответив на первый. Значит, если бы задача была с данным условием и вторым вопросом, всё равно нужно было бы самим ставить первый вопрос и отвечать на него, т. е. задача решалась бы двумя действиями. Аналогичная работа проводится по задаче № 7 (с. 5).

Учебник предлагает также геометрические задачи, которые пом огают разнообразить учебную работу, так как, решая их, дети выполняют измерения (с. 4, № 6) и построения (с. 5, № 8). Пе ред выполнением таких заданий приходится проводить некоторую подготовительную работу. Например, следует вспомнить способы сравнения отрезков: 1) на глаз; 2) наложением («перенеся» один отрезок на карандаш или счётную палочку и приложив его к друг ому отрезку); 3) измерением. На втором уроке полезно вначал е рассмотреть начерченные на доске линии (прямые, кривые — замкнутые и незамкнутые, ломаные); вспомнить всё, что дети зна ют о ломаной. В ходе выполнения задания надо напомнить, как с помощью линейки правильно измерить отрезок и как построить ломаную.

Следует обратить внимание на задание № 8 (с. 4). Так, отвечая на первый вопрос, не все догадываются, что общ ее название треугольника и четырёхугольников — многоугольн ики, так как у некоторых детей 3 или 4 угла не ассоциирую тся с понятием «много». Ещё труднее ответить на второй во прос — надо увидеть, чем похожи каждые две фигуры и чем отличается от них третья (лишняя), т. е. найти и объяснить три варианта решения. Тем не менее с помощью наводящих вопро сов можно выполнить эти задания и объяснить решение так, чтоб ы у детей сложилось убеждение, что они могут решать такие трудные задачи.

При выполнении задания на полях (с. 4) «Разбей на 2 группы» очень важно обратить внимание детей на то, что это задание можно выполнить двумя способами. Один способ — разбиение на 2 группы заданных выражений по знаку действия дети находят без труда. Чтобы они смогли увидеть ещё одно основание для разбиения на 2 группы, достаточно бывает спросить: «Чем число 9 может служить для выражения 6 + 3?»

Таким образом, нетрудно заметить, что структура, содержание и виды деятельности детей на уроке работают на формирование у них УУД: личностных, регулятивных, познавательных и коммуникативных.

Начиная с третьего урока (с. 6) приступают к изучению нум ерации чисел в пределах 100. Прежде всего надо подвести детей к пониманию идеи группировки предметов и возможности считать группы предметов. Учитель может описать такую ситуац ию: садовод срезал много астр и решил их связать в букеты по 5 штук. Сколько букетов у него получилось? На доске можно нар исовать вразброс 20 кружков или выставить их на фланелеграфе. Далее, отсчитывая по 5 кружков, обводят их замкнутой ли нией, т. е. группируют в букеты, и считают. Следует обратить внимание детей на то, что считали, как всегда, но не отдельные астры, а букеты. Дети вспоминают другие примеры счёта групп предметов: ботинки считают парами (говорят: «Купили две пары ботинок», а не «4 ботинка»), пуговицы считают десятками и т. п.

Чтобы показать детям, что при необходимости сосчитать больш ое количество предметов (например, спички или скрепки в кор обке) неудобно все предметы считать по одному, следует отсчит ывать по одному группы по 10 штук, а потом сосчитать десятки. Такую работу можно поручить нескольким «счётчикам» сразу. Ре зультат назовут сами дети (например, пять десятков, или 50 штук).

После таких упражнений можно перейти к работе по учебник у. Выясняют, что ещё считают десятками, читают текст и прис тупают к чтению и записи чисел: 1 дес. — это 10, 2 дес. — это 20 и т. д. После устного выполнения упражнения № 1 (с. 6) можн о записать в тетрадях пару примеров на сложение и вычитание десятков с опорой на рисунки или предложить детям самостоятельно придумать похожую пару примеров.

Заметим, что задания на сложение и вычитание десятков буд ут предлагаться в дальнейшем почти на каждом уроке; это должн о способствовать закреплению не только знаний по нумерации, но и знаний таблицы сложения и вычитания в пределах 10.

На следующем уроке рассматриваются числа, полученные в результате счёта десятков и единиц (с. 7). Вначале можно обрат иться к жизненной ситуации. Например, используя те же круж ки, которые изображали астры на предыдущем уроке, посчитать, сколько букетов астр срезал садовод в другой день. Получают 4 букета и ещё 3 астры. Очень убедительно, на наш взгляд, и такое упражнение: учитель предлагает детям по команде ставить точки на листе бумаги в течение примерно 30 — 40 с. Затем вы ясняют, как быстро и без ошибок сосчитать, сколько точек пос тавил каждый. Дети отсчитывают группы по 10 точек, обводят их замкнутыми линиями и затем сообщают результаты (например, 5 десятков и 8 точек — всего 58). Далее можно выполн ить по учебнику упражнения № 1, 2 и рассмотреть таблицу (с. 7). На этом же уроке можно ввести модели десятков и единиц в виде треугольников и отдельных точек. Рассмотрев рисун ки кубиков (с. 6), дети убеждаются, что если расположить их так, как показано на рисунке (1 + 2 + 3 + 4), то всего получается 10 кубиков, или 1 дес. Затем показывают треугольник, заполненный точками (кружками) по такому же правилу, ко торый будет обозначать десяток. На данном уроке это пособие можно использовать как демонстрационное: дети называют чис ло, которое обозначено треугольниками и отдельными точками, или сами обозначают число с помощью этого пособия.

В дальн ейшем, когда работать практически с пучками палочек будет трудно, рисунки треугольников и отдельных точек помогут детям хорошо усвоить десятичный состав чисел, при этом треугольни ки уже не заполняют точками, договариваясь о том, что нарисо ванные в одну клетку треугольники обозначают десятки, а точки справа от них — единицы. При таком способе детям легко вып олнять рисунки в тетрадях:

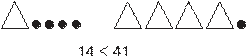
На следующем уроке раскрывается позиционный принцип письм енной нумерации. Чтобы учащиеся поняли и сами сформулиров али правила записи двузначных чисел, как и в 1 классе, использ уют абак (с. 8). В верхний ряд карманов выставляют пучки — десятки и отдельные палочки (или их рисунки), называют число, обозначают цифрами, сколько единиц и сколько десятков оно содержит. Объясняют, что обозначает каждая цифра в записанн ых числах (с. 8, № 2, 3). Особое внимание следует обратить на числа, записанные одинаковыми цифрами (11, 44, 99): пер вая цифра, считая справа налево, обозначает единицы, вторая цифра обозначает десятки. Уже на этом уроке надо показать, что в числе 20 (40, 90) отсутствуют отдельные единицы, но всего единиц в этих числах 20 (40, 90). Это легко увидеть, если за менить десятки единицами (т. е. развязать пучки и сосчитать па лочки по одной).

Следующий урок (с. 9) отведён закреплению знаний по нум ерации. Дети читают и записывают числа, образуют числа из десятков и единиц, называют десятичный состав двузначных чис ел, объясняют значение цифр в записанных числах.

Вводятся понятия и термины «однозначное число» (содержит только единицы и записывается одной цифрой) и «двузначное число» (обязательно содержит десятки, записывается двумя циф рами, поэтому 01, 02 не являются двузначными числами). Так как, рассматривая ряды чисел (с. 9, № 2), ученики встретятся с числом 100, то можно обратить внимание на его запись: использ ованы три цифры, это самое маленькое трёхзначное число, перв ое в ряду трёхзначных чисел.

Сравнивая двузначные числа (с. 9, № 3), дети опираются на десятичный состав этих чисел: 16 — это 1 дес. и 6 ед., 60 — это 6 дес., 1 дес. < 6 дес., значит, 16 < 60. Так как назван ия этих чисел схожи (многие дети не различают их на слух), следует и в дальнейшем почаще включать в устные упражнения сравнение чисел второго десятка с числами круглых десятков (13 и 30, 15 и 50 и т. п.).

Как и в 1 классе, в учебнике регулярно включаются упражнения для работы детей в парах, что требует чёткой организации этой работы (что и как делать, как контролировать и оценивать результаты, с. 9, 10, 11, 15 и далее).

Известно, что только деятельность систематическая, правильно организованная, целенаправленная (помогать друг другу учиться) формирует коммуникативные УУД (см. с. 136 данного пособия).

Урок, на котором дети будут знакомиться с новой единицей длины — миллиметром (с. 10), также следует использовать для закрепления знаний по нумерации. Например, можно предложить составить и записать числа, используя три заданные цифры (2, 4, 9 и 0, 5, 8), выяснить, почему во втором случае можно состав ить только 4 числа, а не 6, как в первом случае. Попутно по вторяют десятичный состав, правила записи двузначных чисел, место отдельных чисел в натуральной последовательности. Подв одя учащихся к теме урока, можно поработать с моделью метр а («лента ста»), на которой выделены дециметры и сантиметры (её можно изготовить из картона):

— Назовите длину отрезка в сантиметрах (показать  3 дм, 5 дм, 9 дм 5 см и т. п.).

— Покажите на этой линейке отрезок длиной 40 см  (66 см, 71 см) и скажите, сколько в длине этого отрезка уложилось де циметров (дециметров и сантиметров).

Далее можно перейти к работе по учебнику (№ 1—3, 7). Важно выяснить, зачем нужны более мелкие единицы измерения (попутно и более крупные). Учащиеся без особых затруднен ий отмечают необходимость выбора мерки, удобной для измер ения. Следует также обратить внимание на то, что использован ие двух мерок повышает точность измерения (с. 10, № 2). Срав нение двух значений длины (с. 10, № 3) полезно выполнять с использованием линейки («Найдите на линейке отрезки дли ной 1 см и 9 мм. Какой из них длиннее? Запишем: 1 см > 9 мм, поясним во второй строке: 10 мм > > 9 мм»). Ана логично: 2 см 1 мм < 3 см, 21 мм < 30 мм.

На следующем уроке важно не только закрепить знания по нумерации (с. 11, № 1, 4), но и показать практическую зна чимость изучаемого материала, возможность использования счё та и измерения в жизни. Многие учителя предлагают детям с сам ого начала изучения темы узнать у родителей или выписать из книг интересные сведения («Двузначные числа вокруг нас») и рассказать об этом в классе. Например, на одном из таких уро ков дети сообщили: «В нашем доме 50 квартир», «В деревне у бабушки выросла тыква весом (массой) 20 кг».

Предлагаются практические упражнения в измерении (с. 11, № 2, 3). Можно также показать, как определяют размер рубаш ки по длине ворота.

Аналогичные задания можно включить и в следующий урок (с. 12). При выполнении данных в учебнике упражнений важно ещё раз подчеркнуть, что при изменении места цифры в записи числа изменяется её значение (с. 12, № 2, 3, 4).

При ознакомлении с метром (с. 13) легко подвести детей к необходимости иметь более крупные единицы длины, чем все им известные. Например, детям понятно, что длину и ширину класса неудобно измерять мелкими мерками. Полезно воспроизв ести практически все изученные единицы длины: изобразить в тетради и записать соотношения (10 мм = 1 см, 10 см = 1 дм). Метр — известная большинству учащихся мерка, они видели, как метром отмеривают ткани. Кроме того, у них есть представл ение о метре, так как они работали с «лентой ста». Опираясь на модель метра, легко установить, что 10 дм составляют 1 м. Для закрепления материала дети читают по учебнику таблицу и находят в классе расстояния, примерно равные метру. На уроке труда или дома дети изготавливают модель метра, чтобы затем использо вать её на практике (с. 13, № 1).

Следующие уроки (с. 14, 15) отводятся на закрепление изуч енного материала. В частности, знание десятичного состава двузначных чисел применяется при сложении и вычитании вида 30 + 5, 35 – 5, 35 – 30, а также при замене числа суммой раз рядных слагаемых (36 = 30 + 6). Важно, чтобы, выполняя такие задания, дети не только называли ответ, но и давали пояснения: 3 дес. и 5 ед. — это число 35, из 3 дес. 5 ед. вычтем 5 ед., получим 3 дес., или 30, и т. п. Некоторые дети, не усвоив приёма вычисления, пытаются присчитывать и отсчитывать по одному или по частям и, конечно, допускают ошибки. На этих уроках в кач естве опоры (особенно для слабоуспевающих детей) надо исп ользовать действия с любыми моделями десятков и единиц (с. 14), а также карточки с записью разрядных чисел: 10, 20, ..., 90; 1, 2, ..., 9 (с. 15).

Умение оперировать разрядными числами — основа устных приёмов вычислений, поэтому, несмотря на кажущуюся лёгкость, задания на сложение и вычитание разрядных чисел, а также на замену двузначного числа суммой разрядных слагаемых должны включаться систематически в устные упражнения и в решение задач.

Указанные умения закрепляются, когда приходится вести рас чёт монетами разного достоинства (с. 16, № 1—3; с. 17, № 3), а также выполнять преобразование величин. Например, надо сравн ить 2 м 8 дм и 30 дм. Объяснение: 2 м — это 20 дм да ещё 8 дм, всего 28 дм, 28 < 30, значит, 2 м 8 дм < 30 дм (можно рассуждать и по-другому:

30 дм — это 3 м, 2 м < 3 м).

Желательно на уроках закрепления (с. 16, 17) связывать вопросы по нумерации и измерению величин, придавая упражнен иям практическую направленность. Например, на доске даются рисунки монет: 10 р., 5 р., 2 р., 1 р. — и купюр (два прямоугольника): 50 р. и 100 р. (можно показать соответствующие купюры). Детям предлагают такие задания:

— Сколько может быть денег у мальчика, если у него  1 купюра и 1 монета? 2 купюры и 1 монета? 2 купюры и 3 монеты?

— Как можно разменять купюру в 100 рублей одинако- выми купюрами? купюрами и монетами?

Для закрепления знаний порядка следования чисел при счёте можно использовать такие жизненные ситуации:

— Какое сегодня число? А какое число было вчера?  поза вчера? Какое число будет завтра? послезавтра?

— На каждом этаже 4 квартиры. Номер одной из квар- тир на первом этаже 38. Какие номера квартир могут быть ещё на этом этаже (записать несколько вариантов)? Если 38 — это номер последней квартиры на первом этаже, то на каком этаже нахо дится квартира номер 45?

— Девочка читает книгу на странице 50. Назовите но- мера предыдущей и следующей страниц.

На уроках закрепления «Что узнали. Чему научились» ис пользуются упражнения со с. 20, 21. Если самостоятельные работы будут успешными, то можно провести контрольную работу по тем е. В противном случае следует продолжить закрепление материала на уроках при изучении следующей темы «Сложение и вычита ние», тем более что до конца первой четверти новых приёмов вычислений не вводится, а через одну-две недели знания по ну мерации с помощью систематических упражнений будут усвоены всеми учащимися.

Для самоконтроля и самооценки результатов изучения темы «Нумерация» используются предметные тесты с выбором ответа (с. 22, 23).

На протяжении всего периода изучения нумерации (по суще ству, весь сентябрь) значительная часть каждого урока отводитс я закреплению вычислительных навыков. Как уже отмечалось, с этой целью в уроки включаются игры и занимательные упражн ения, а также устные упражнения (8—10 мин), когда отдельн ые учащиеся называют результаты. Более эффективно, когда обеспечивается обратная связь и дети показывают ответы разр езными цифрами. Удобно использовать самодельный или покуп ной «числовой веер» либо «ромашку» из скреплённых карточек с цифрами. Возможны разнообразные формулировки заданий: — Первое слагаемое — 7, второе — 4. Чему равна сумма?

— Чему равна разность чисел 12 и 3?

— Увеличьте (уменьшите) 9 на 6.

— Дополните до 10 числа 9, 7, 6.

— Сколько надо получить сдачи с 10 рублей, если по- купка стоит 5 рублей? 6 рублей? 8 рублей?

— Сколько надо прибавить к 7, чтобы получилось 12?  Скольк о вычли из 15, если получилось 9? (Запись на доске имеет вид 7 +  = 12.)

— Верно ли, что если из числа вычесть это же число,  то по лучится 0? Приведите свои примеры. И т. п.

При этом следует учесть, что числа, над которыми должны выполняться действия, дети с трудом удерживают в памяти, ес ли подобные задания предлагаются на слух, поэтому учителю на до либо показывать числа на разрезных цифрах, либо записы вать их на доске.

Учебник содержит обширный материал для устных упражне ний: ребусы (с. 9), состав чисел (с. 10, 11, 16), пример-цепоч ка (с. 14), игра «Составим поезд» (с. 15), игра «Поднимись по лесенке» (с. 16), набор монет (с. 17, поля), игра «Узнай побе дителя» (с. 20, № 3), игра «Найди лишнюю сумму» (с. 21) и т. д. Данные упражнения помогают быстро и эффективно орг анизовать работу, так как дети воспринимают их и зрительно, и на слух. Кроме того, на основе этих упражнений можно предла гать аналогичные задания.

При работе над вычислениями не следует упускать возмож ности формировать у детей познавательные УУД: развивать наблюдательность, догадку, привычку вним ательно воспринимать учебный материал. Хорошие результаты в этом плане даёт такой приём: до того как решать любые прим еры из учебника, учитель предлагает детям внимательно расс мотреть все столбики и рассказать, что они заметили. Так, рас сматривая примеры задания № 4 (с. 6), дети отмечают, что есть пример ы в одно действие, а есть в два; есть примеры, где нужно выполнить только сложение или только вычитание, а есть при меры, где надо и складывать, и вычитать. Такие задания приуча ют детей анализировать материал.

Для формирования приёма сравнения полезно сопоставлять столбики примеров или примеры в отдельном столбике (опреде лять, чем они похожи и чем различаются). Так, в № 4 (с. 6) можно сравнить примеры в первом столбике и, не вычисляя, ска зать, в каком из них ответ будет меньшим и почему. Или до ре шения примеров найти такой столбик, который отличается от всех остальных (с. 7, № 5; с. 9, № 6; с. 12, № 9 и др.). Очень хор ошо, если дети выполнят это задание по-разному и приведут свои пояснения. Так, рассматривая примеры в № 6 (с. 9), один ученик скажет: «Третий столбик отличается от всех остальн ых, он на сложение, а все остальные на вычитание», другой наз овёт пятый столбик, так как в нём выполняются действия над двузначными числами, оканчивающимися нулём (круглыми десятк ами), кто-то может выделить четвёртый столбик и т. п. Возвращ аясь к № 4 (с. 6), можно дать задание: найти в четвёртом столб ике пример, который отличается от двух других, и решить его (17 – 17 + 8 = 0 + + 8 = 8). Часто это задание формулируется так: найти лишний столбик, лишний пример (в заданиях по геометрии — лишнюю фигуру).

На основе умения сравнивать формируется умение классифи цировать, которое тоже можно развивать, опираясь на вычислит ельные задания: детям предлагают разбить данные примеры на 2—3 группы и сказать, по какому признаку выделены эти груп пы, или спросить их: «На какие группы можно разбить эти примеры и почему?» Например, на уроке, где вводятся понятия однозначного числа и двузначного числа (с. 9), после того как дети выполнили задание № 6 на сравнение (нашли столбик при меров, который отличается от всех остальных), можно предло жить задание на классификацию.

Из всех вариантов разбиения примеров на группы выбирают такой: в одних примерах в ответах получаются однозначные числа, в других — двузначные. Зат ем выписывают и решают примеры только одной группы. При проверке можно выяснить, почему одни примеры выписали, а другие нет.

Особенно детям нравятся задания, в которых предлагается, рассмотрев какой-то столбик примеров, подметить определённую закономерность и составить самим похожие примеры (с. 12, № 9; с. 14, № 6; с. 15, № 5 и др.). Такие задания формир уют у детей умение обобщать. Так, после анализа примеров из № 9 (с. 12) можно остановиться на третьем столбике и предл ожить детям отметить, чем интересны эти примеры (складыва ют два одинаковых однозначных числа и вычитают 10). Затем предлагают составить свои примеры так, чтобы продолжить этот столбик. Интересно обсудить, почему не подходят прим еры 10 + 10 – – 10, 11 + 11 – 10, а почему подходит как продол жение вверх пример 5 + 5 – 10.

Вначале, естественно, такую работу проводят коллективно (по вопросам учителя, с записью на доске), затем можно предложить выполнить задание, работая в паре, а позже — на выбор: можно решить примеры из учеб ника, а можно составить похожие примеры самому и решить их.

Как видно, не очень сложно усилить развивающую роль выч ислительных упражнений. Важно включать подобные задания сис тематически, формируя у детей интерес, желание и умение на блюдать и обсуждать замеченное. Однако ввиду ограниченности времени на уроке приходится отбирать из многочисленных разв ивающих заданий (которые приводятся в статьях журнала «Нач альная школа», сборниках упражнений, альтернативных учебни ках) только минимум доступных большинству учащихся данного класса и так, чтобы успеть поупражнять детей в вычисл ениях.

На каждом уроке, отведённом на изучение нумерации, идёт работа над задачами. Вначале решаются простые задачи (с. 6—10). Это задачи на нахождение суммы и остатка, на увел ичение и уменьшение числа на несколько единиц, на разностн ое сравнение. Когда числовые данные позволяют, можно при выборе действия опираться на схему (с. 7, № 3, 4). К задачам дети рисуют картинки с точками или работают с фишками, по ясняя: мальчиков на 2 больше, чем девочек, значит, берём стольк о кружков, сколько треугольников, и ещё 2 (№ 3); девочек на карусели на 2 меньше, чем мальчиков, значит, их было столько же, сколько мальчиков, но без 2 (№ 4). Схемы к этим задачам выглядят так:

Опираясь на схемы, легко сравнить задачи и их решения.

В задачах на разностное сравнение (с. 8, № 6) важно, чтобы дети понимали, что ответ задачи (разность) имеет двоякий смысл: решив задачу, мы отвечаем на два вопроса (журнальный столик на 2 дм ниже письменного, а письменный стол на 2 дм выше журнального).

К простым задачам в учебнике предлагаются различные творч еские задания: составить задачи по краткой записи; дополнить вопрос или условие, чтобы получилась задача; изменить вопрос так, чтобы задача решалась другим действием, и т. п. В числе простых задач для устного решения надо давать задачи с недо стающими и лишними данными, с вопросом, который находится в начале или в середине задачи. Например:

— Сколько рублей не хватает Юре, если у него есть  10 руб лей, а книга стоит 13 рублей?

— В этом году Диме исполнилось 7 лет. Сколько лет  его брату, если он младше Димы на 2 года?

В это же время рассматривают задачи, подготавливающие де тей к решению составных задач. Это задачи с двумя вопросами (с. 8, № 5), задачи-цепочки (с. 9, № 5). Надо обратить внима ние детей на особенности этих задач (нельзя решить вторую задачу, пока не решишь первую). После решения можно сформ улировать составную задачу, объединив эти две простые.

Постепенно в уроки начинают включать составные задачи (с. 11 и далее). Чтобы дети не смешивали простые и составные задачи, важно научить их после чтения зада чи выделять условие и вопрос, спрашивать себя: «Можно ли сразу (одним действием) ответить на вопрос задачи?» Если мож но — выбираем действие и решаем задачу, а если нельзя — составляем план решения, т. е. говорим, что узнаем сначала (первым действием), а что узнаем потом (вторым действием). На первых порах это подробное пояснение дети выполняют с помо щью учителя.

Чтобы дети включили составление плана решения в рассужд ение при решении задач, целесообразно чаще выполнять рабо ту над задачей по цепочке:

1.                   Читаю задачу (сначала все дети читают про себя, а затем один ученик вслух).

2.                   Называю условие (что известно).

3.                   Называю вопрос (что надо узнать).

4.                   Объясняю (сразу ответить на вопрос задачи нельзя, так как не знаю...).

5.                   Составляю план решения (первым действием узнаю... ,вторым действием узнаю...).

6.                   Решаю.

7.                   Называю ответ.

Как показывает практика, особенно в начале учебного года, надо чаще предлагать задания на сравнение простой и составной задач — с одинаковым условием, но разными вопросами: «Сколь ко страниц занимает вторая сказка? Сколько страниц занимают две сказки?» (с. 13, № 4). Полезны задания на преобразование простой задачи в составную и наоборот. Например: «Поставьте во прос так, чтобы задача решалась одним действием» (с. 12, № 6).

Скажем несколько слов о задачах на смекалку. На с. 9 дана задача, которая решается методом перебора. Предлагается сос тавить и зарисовать наборы из двух овощей, выбирая их из че тырёх данных (можно предложить в качестве домашнего задан ия). Чтобы сократить время, можно обозначить овощи начальн ыми буквами их названий (С, М, О, П). Главное, в любом слу чае обратить внимание детей на систему составления пар. На пример, берём первый элемент и составляем пары с остальным и, затем берём второй и также составляем пары с остальными, отбрасывая уже состав-ленную пару, и т. д. Затем подсчитываем получившиеся пары (6). Аналогично решается задача № 15 (с. 73). Кроме того, есть задачи, которые решаются подбором (с. 18). Здесь приходится учитывать ряд условий. Помогают в подборе иллюстрации, схематические записи. Например, к пер вой задаче можно дать такую запись:

Пусть будет один ёж, тогда зайцев будет 6, а белочек 14 – 6 – 1 = 7. Не подходит, так как по условию больше всех был о зайцев. Проверяем так же число 2 — оно подходит.

После повторения основных вопросов темы (с. 20, 21) и выполнения детьми предметного теста (с. 22, 23) можно провести контрольную работу.

КОНТРОЛЬНАЯ РАБОТА

В        содержание          контрольной           работы        по       теме

«Нумерац ия в пределах 100» можно включить следующие задания:

1. Арифметический диктант.

1)       Запиши числа: 15, 50, 70, 17, 100.

2)       Запиши число, в котором 3 дес. 8 ед. (8 дес. 3 ед.).

3)       Сравни числа 67 и 76, вставь знак >, < или =.  4) Запиши число 92. Вычитая из него по одному,  запиши ещё 5 чисел.

 5) Вставь пропущенное число: 1 м =  см (1 р. =  к.).

2.    Реши задачу.

3.    Реши примеры.

69 + 1        5 + 30                    56 – 506 + 40                    49 + 1          34 – 4 

40 – 1        89 – 9                  20 + 60 78 – 70                  90 – 1          60 – 20

4. Дополнительное задание (по желанию).

Запиши число, в котором десятков и единиц поровну (десятк ов больше, чем единиц; десятков меньше, чем единиц).

Сложение и вычитание

Выделим в этой теме три этапа: первый — пять неде ль в первой четверти (см. «Тематическое планирование», с. 140—141); второй — семь недель во второй четвер ти, когда изучаются приёмы устных вычислений; третий — окол о пяти недель в третьей четверти, отведённых изучению приё мов письменных вычислений.

В содержание первого этапа включены знакомство с задачам и, обратными задачам на нахождение суммы и остатка; работа над выражениями (понятие числового выражения, порядок дейс твий, сравнение выражений, запись решения составной задачи выражением); изучение переместительного и сочетательного свойств сложения и их использование для рационализации выч ислений. Как видно, знания детей о сложении и вычитании знач ительно углуб-ляются. Кроме того, в это время закрепляются знания по нумерации и отрабатываются навыки табличного сло жения и вычитания. Всё это создаёт прочную базу и готовит дет ей к изучению приёмов вычислений с двузначными числами. К концу первой четверти учащиеся:

•         усвоят понятие задачи, обратной данной, приобретут опыт в составлении и решении задач на нахождение неизвестного слаг аемого, неизвестного уменьшаемого, неизвестного вычитаемого;

•         усвоят понятие числового выражения, научатся читать и записывать числовые выражения в два действия, находить значения выражений со скобками и без них, сравнивать два выражения, записывать решение составной задачи вы ражением;

•         познакомятся с новой единицей времени — минутой, узнают, что в 1 ч 60 мин, научатся определять по часам время с точностью до минуты;

•         узнают разные способы нахождения длины ломаной и пери метра многоугольника, применят эти знания при решении задач;

•         усвоят сочетательное свойство сложения, применят переместительное и сочетательное свойства сложения для рацио нального выполнения вычислений.

Наглядные пособия

Дополнительно к тем наглядным пособиям, которые использ овались при изучении нумерации, можно приготовить образцы краткой записи задач, а также циферблат с подвижными стрел ками для упражнений в определении времени по часам. Для из мерения длины ломаной учителю и детям потребуется не только линейка, но и циркуль.

Рассмотрим работу над задачами.

На первом уроке по теме вводится понятие задачи, обратн ой данной. В учебнике предлагается рассмотреть три взаимно обратные задачи (с. 26, № 1), их краткие записи и на этой осн ове сформулировать вывод, как составляют обратные задачи. Решив исходную задачу, надо взять её ответ и включить его в новую задачу, не меняя сюжета, а одно из известных сделать искомым. Если класс подготовлен, то можно отметить, что перв ая задача была на нахождение суммы, а вторая и третья — на нахождение одного из слагаемых. Для закрепления проводится аналогичная работа ещё над одной задачей.

Можно ввести понятие задачи, обратной данной, не на гото вых задачах, а в процессе составления детьми обратных задач к задаче на нахождение суммы, т. е. вначале коллективно порабо тать над задачей № 2 (с. 26), выполняя краткие записи на доске и в тетрадях, а затем для закрепления рассмотреть за дачу № 1.

Для предупреждения неверного обобщения (исходная задача решается сложением, а обратные ей — вычитанием) полезно в качестве закрепления дать задачу на нахождение остатка и обр атные ей (на этом или следующем уроке):

Было — 10 кн.   ?                                                 10 кн.

Взяли — 4 кн.   4 кн.  ?

Осталось — ?                                   6 кн.  6 кн.

Пусть дети сравнят задачи и увидят их сходство и различия.

На следующем уроке (с. 27), кроме закрепления понятия об ратной задачи, проводится работа с отрезками, что очень важно для иллюстрирования задачи с помощью чертежа. Вначале рассматривают сложение отрезков. Можно предложить ученикам самим начертить два отрезка (например, длиной 4 см и 5 см) так, чтобы конец первого был началом второго. Длину отр езка-суммы можно найти по-разному: 1) измерением; 2) сложен ием длин отрезковслагаемых (4 см + 5 см = 9 см) — и убедитьс я, что получились одинаковые результаты.

Выполняя второе задание из № 1 (с. 27), дети знакомятся с вычитанием отрезков. Здесь также можно найти результат и изм ерением, и вычислением (из длины большего отрезка вычитают длину меньшего: 10 см – 4 см = = 6 см). Для закрепления выполн яется задание № 5

(с. 27). Заметим, что если у детей нет цир кулей, то они пользуются одним из способов нахождения разно сти отрезков, а именно находят длину наибольшей и наименьшей сторон четырёхугольников и из большего значения вычитают мень шее. Если циркули есть, то с их помощью откладывают меньший отрезок на большем и измерением находят длину разности отр езков.

Следующие два урока отводятся знакомству с задачами на на хождение неизвестного уменьшаемого и неизвестного вычитаемо го. Учебник предлагает вводить их последовательно. Если класс хорошо подготовлен (большинство детей хорошо владеет термин ологией, а также свободно составляет задачи, обратные данной), то можно избрать и другой подход — ввести эти задачи на од ном уроке как обратные задаче на нахождение остатка. Однако и в том случае, когда новые виды задач вводятся последователь но, полезно установить связь со знакомыми задачами, сравнить их и тем самым предупредить ошибки в решении задач. Известн о, что дети часто решают новые задачи как задачи на нахожде ние остатка, подставляя искомое число в решение.

Можно начать работу над новым материалом (с. 28) сразу с новой задачи: прочитать её, рассмотреть рисунок, краткую зап ись, составить схему или чертёж, выяснить, почему нужно объе динять кружки или складывать отрезки, обозначающие те ма шины, которые остались, и те, которые уехали; записать реше ние: 6 + 3 = 9 (м.). Затем составить задачу, обратную данной (на нахождение остатка), сделать к ней краткую запись, записать реш ение: 9 – 3 = =  6 (м.). Сравнивая краткие записи, а также реш ения задач, дети увидят, что новая задача — это задача, обр атная задаче на нахождение остатка. Для закрепления проводится аналогичная работа над задачей № 2 (с. 28).

При решении задач на нахождение неизвестного уменьшаемого и неизвестного вычитаемого дети могут опираться для выбора действия либо на привычные схемы, заменяя предметы фишками (точками, кружками и т. п.), либо на готовые схематические чертежи, которые даются в учебнике или на доске.

Следующий урок (с. 29) можно начать с решения задачи: «В коробке было 10 карандашей. Коля взял из коробки 4 ка рандаша. Сколько карандашей осталось в коробке?» Сделать вместе краткую запись задачи, выбрать из трёх предложенных соответствующую схему или чертёж. Решение дети выполняют самостоятельно. Затем следует прочитать задачу № 1 (с. 29), рассмотреть её краткую запись, установить, что это задача, об ратная только что решённой. Чертёж поможет детям правильно выбрать действие.

Задача № 2 (с. 29) — на нахождение неизвестного уменьшаемого — решается сложением, следовательно, к ней подходит схематический чертёж, на котором изображено сложение отрезков. По другому чертежу составляют задачу на нахождение остатк а: «У Тани было 7 значков. Она подарила подруге 2 значка. Сколько значков осталось у Тани?»

При наличии времени можно состав ить и решить другую обратную задачу к задаче № 2 (с. 29) — на нахождение вычитаемого. Краткую запись и чертёж к ней учитель в процессе беседы с детьми выполнит на доске.

Следующий урок отводится закреплению умения решать задач и на нахождение неизвестного уменьшаемого и неизвестного вы читаемого (с. 30). Опираясь на схемы, дети выполняют решение практически (либо рисуют, либо действуют с фишками), объяс няя каждый раз выбор действия: из 12 фишек убираем 7, так как 12 фишек обозначают всех овец — и тех, которые убежа ли, и тех, которые остались. Значит, задача решается вычитани ем. В другой задаче, обозначив точкой (кружочком) одну овцу, рисуют 3 точки (столько овец убежало) и ещё 8 точек (столько овец осталось). Объединив все точки, видят, что всего овец 3 да 8. Значит, задача решается сложением. Аналогично используют готовые чертежи, которые могут быть даны учителем на доске.

Не стоит устанавливать отношение «больше (меньше)» межд у данными и искомым: «Было овец больше или меньше, чем осталось? Убежало овец больше или меньше, чем...?» Детям трудн о понять, что с чем сравнивать. Действительно, чтобы обоснов ать вычитание при нахождении вычитаемого, легче увидеть дру гое отношение: уменьшаемое состоит из вычитаемого и остатка, поэтому, чтобы найти вычитаемое, надо из уменьшаемого вычесть остаток. Хотя этот вывод будет сформулирован намного позднее, он лежит в основе тех действий, которые дети выполняют с помощью практических операций. Некоторые методисты рекомен дуют при решении этих задач устанавливать связь между целым и частью и даже формулируют выводы: чтобы найти целое, надо сложить части; чтобы найти часть, надо из целого вычесть изв естную часть. Однако наблюдения показывают, что дети не только применяют эти выводы к задачам на сложение и вычитание, но и пытаются использовать их при решении задач на умножение и деление.

С нашей точки зрения, полезнее накапливать опыт выполнен ия практических операций при решении задач на нахождение неизвестного слагаемого (уменьшаемого, вычитаемого). Это бу дет служить подготовкой к усвоению связей между результатами и компонентами сложения и вычитания и их формулировками: если из суммы вычесть одно из слагаемых, то получится другое слагаемое; если к разности прибавить вычитаемое, то получится уменьшаемое; если из уменьшаемого вычесть разность, то получится вычитаемое (с. 86—87). Для проверки правильности выч ислений, а в дальнейшем для решения уравнений достаточно, если при решении подобных задач на первых уроках дети не станут ориентироваться на единственное слово («уехали», «убе жали» — значит, надо вычитать) и поймут, что в этих задачах надо внимательно разбирать, что известно, а что надо узнать, и, чтобы решить правильно, полезно опираться на схему или чертёж.

Обратим внимание учителя на то, что на этом этапе изучен ия темы «Сложение и вычитание» учебник предлагает исполь зовать составление и решение задачи, обратной данной, как способ проверки решения простой задачи (с. 45, № 4). Предполагает ся, что к этому времени дети научатся составлять обратные задачи. Теперь характер объяснения меняется — ученик рассказ ывает, не как он составил обратную задачу, а что показало её решение. Если, решив обратную задачу, получаем число, которое было известным в исходной задаче, значит, исходная задача реш ена правильно.

Наряду с простыми задачами (решаемыми в одно действие) продолжается работа над составными задачами. Вначале их реш ение по-прежнему записывают по действиям, устно объясняя, что узнавали каждым действием (с. 27, № 2; с. 30, № 4 и др.). В уроки включаются упражнения на сравнение простых и составн ых задач (с. 55, № 25), на преобразование составной задачи в простую, на составление задач по рисунку и краткой записи и др. (с. 30, № 2 и др.). Все эти творческие задания помогают формировать познавательные УУД.

После введения понятия числовое выражение показываетс я запись решения составной задачи выражением (с. 40, № 4). Если класс недостаточно подготовлен, то не следует форсировать этот способ записи решения задач. Полезнее подольше работать с готовыми выражениями: «Выбери то выражение, которое мож но составить для решения данной задачи; объясни, как рассужд али дети, если они при решении одной и той же задачи состав или два разных выражения» (с. 41, № 2; с. 42, № 4). Здесь следует пояснить, что эти задачи решены разными способами, и обратить внимание детей на то, что оба способа правильны, так как получился один и тот же ответ, хотя рассуждали по-разному.

Можно также предлаг ать для выбора правильно и неправильно составленные выра жения. Например, к задаче № 4 (с. 40) дать задание выбрать решение из выражений 6 + (6 + 2) и 6 + (6 – 2).

Многие учителя используют в этот период такой приём — предлагают детям самим выбрать способ записи решения: кто хо чет — выражением, кому трудно — по действиям. При проверк е записывают решение в виде выражения на доске и предлага ют пояснить, что узнавали первым действием, что — вторым. После объяснения решение в виде выражения могут записать и те дети, которым было трудно это выполнить самостоятельно.

Важно с первых шагов чётко различать разные способы решения (когда различается ход рассуждений при решении задач и) и разные способы записи решения. В последнем случае ход рассуждения, а следовательно, и план решения задачи одинаков ые, но в одном случае записывают и выполняют отдельные дейс твия, а в другом сначала обозначают все действия в одном выражении, а затем находят значение этого выражения. Запись решения задачи сначала по действиям, а затем одним выражением в начале работы над новым видом задач у мно гих детей вызывает затруднение, т. к. предполагает переход от развёрнутого пояснения действий к краткому. Поэтому, для того чтобы учащиеся осознанно выбирали действия при решении задач, не следует форсировать этот переход, особенно у слабо подготовлен ных детей.

Так как уже изучены числа в пределах 100, то и в задачах появляются числа, изображать которые с помощью схематичес кого рисунка становится нецелесообразным. К этому времени дети уже научатся чертить отрезки, научатся складывать и вычитать их (с. 27), поэтому постепенно можно переходить к иллюстрированию задачи с помощью чертежа. Готовые чертежи приводятся сначала к простой задаче (с. 39, № 5), а затем к со ставной (с. 43, № 5). В дальнейшем следует давать готовые чертежи с записью на них числовых данных (с. 46), а также без них — с предложением детям самим обозначить данные и искомые числа на чертеже. Полезны задания на выбор чертежа к данной задаче, когда на доске предлагаются правильно и не правильно выполненные чертежи. К построению чертежей самими детьми надо переходить постепенно, так как это заним ает много времени на уроке, а также требует от детей дос таточного опыта.

Рассмотрим линию работы над сложением и вычитанием.

В каждый урок включаются устные и письменные упражнения на отработку вычислительных умений и навыков. Это табличные слу чаи сложения и вычитания — так называемые нумерационные случ аи (69 + 1, 90 – 1, 40 + 7, 47 – 40, 47 – 7), сложение и вычит ание круглых десятков (60 + 20, 90 – 30), сложение и вычитание с нулём. Числовой материал подобран так, что до решения примеров можно предлагать задания, направленные на формиро вание умений анализировать («Рассмотрите все примеры и скажите, что вы заметили»); сравнивать («Чем похожи и чем разл ичаются столбики или примеры в отдельных столбиках?»); клас сифицировать («На какие группы можно разбить все эти прим еры?»); обобщать («Рассмотрите, как составлены примеры в столбике, и составьте свои примеры по этому же правилу»). Про должить столбики своими примерами в учебнике предлагается достаточно часто, такая возможность обозначается многоточием (с. 26, № 4; с. 28, № 4; с. 29, № 5 и др.). Данные упражнения удобно использовать для дифференцированного обучения: одни дети решат только те примеры, которые даны в учебнике; другие составят и решат столько примеров, сколько смогут за отведённое учителем время.

Для подготовки детей к введению выражений со скобками (с. 38) в учебнике предлагается заблаговременно включать в уст ные упражнения как можно чаще такие задания, например: «Найди сумму (разность) чисел 6 и 4 и прибавь её к числу 20» и т. п. При этом можно использовать на доске записи, в которых сумма (разность) выделена, например, овалом (с. 34, № 2). Такая подготовительная работа поможет детям нау читься читать и записывать выражения со скобками.

К использованию скобок можно подвести так, как предлага ется в учебнике: рассмотреть образцы прочитанных и записан ных примеров и, опираясь на правило, учить читать и решать так ие примеры (с. 38, № 1—3). При чтении помогает такая Памятка:

1.       Посмотри на знак в скобках и скажи, это сумма или разность.

2.       Посмотри на другой знак и скажи, надо прибавить или вычесть.

3.       При чтении надо также следить за предлогами:

«прибавить к...», «вычесть из...».

Можно ввести скобки и по-другому — предложить детям самим составить примеры, используя числа, знаки «+», «–» и сумму (разность), записанные на карточках. Выполняя действия, дети могут получить разные результаты: 10 – 7 + 2 = 1 или 10 – 7 + 2 = 5. Чтобы избежать этого и показать, что из 10 выч итают сумму, используют общий знак — скобки. Договарива ются, что в таких примерах сначала находят сумму (разность), т. е. первым выполняют действие в скобках.

Работая с заданием № 2 (с. 38), дети методом проб находят место скобок. Например, 4 – 1 + 2 = 1. Пробуем к разности 4 – 1 прибавить 2, получаем 5, а не 1 (не подходит). Тогда за ключаем в скобки сумму чисел 1 и 2, из 4 вычитаем 3, получаем 1. Записываем: 4 – (1 + 2) = 1, читаем: «Из числа 4 вы честь сумму чисел 1 и 2, получится 1». (Это легче и понятнее, чем «Из четырёх вычесть сумму одного и двух...».)

Естественно, за один и даже за несколько уроков дети не на учатся читать и записывать примеры со скобками, но в процес се длительных упражнений с помощью учителя эти умения сформ ируются (только не надо читать, называя отдельные числа и знаки: 10, плюс, скобка открывается и т. д.).

Теперь, когда дети знакомы с разными примерами — в одно и два действия, со скобками и без скобок, — можно ввести по нятие и термин выражение.

Предложенные записи (с. 40, № 1) включают все известные детям примеры, в которых разн ые числа (однозначные и двузначные) соединены знаками «+» и «–» в различных сочетаниях. Рассматривая с детьми данные столбики примеров, надо выявить все эти особенности. Безус ловно, можно предложить учащимся самим составить и записать разные примеры, используя четыре-пять чисел, знаки действий и скобки, а затем сравнить и выявить существенные признаки (это записи, состоящие из разных чисел, соединённых разными зна ками действий, которые могут включать скобки).

Новые термины постепенно войдут в речь детей, если учитель будет их активно использовать. Не стоит тратить много времени и сил на то, чтобы дети быстро перешли на новую терминолог ию. Пусть наряду с новыми фразами — «запишу выражение», «найду значение выражения» — звучат привычные — «запишу пример», «решу пример». Однако надо настойчиво исправлять, если дети будут смешивать эти фразы и говорить: «Запишу выражение и решу его».

Чтобы учащиеся усвоили новое понятие, надо начать оперир овать им. На первом же уроке дети читают и записывают вы ражения, находят их значения; выбирают выражение, составленн ое по данной задаче. На следующем уроке учатся сравнивать выражения (с. 41). Основным способом сравнения является сравн ение значений выражений, т. е. надо вычислить значения заданн ых выражений, сравнить числа и сделать на этой основе вывод о соответствующем отношении выражений («Вычислю..., вычислю..., сравню числа..., поставлю знак...»).

Важно, чтобы, после того как будет сделан вывод и поставлен знак, дети читали полученное равенство или неравенство («Разность чисел 5 и 2 меньше, чем сумма чисел 1 и 4»). Позже полезно предлагать и такие выражения, которые можно сравнить, не вычисляя их знач ения, а выясняя, чем они похожи и чем различаются.

Но после того как объяснение прозвучало, надо для проверки всё-таки выполнять вычисление. Учителя иногда формулируют это как тре бование к оформлению заданий подобного рода: «Сравнение вы ражений всегда записывайте в две строки».

Важным моментом является знакомство не только с переместительным, но и с сочетательным свойством сложения. Рассматривая сложение трёх слагаемых (с. 44, № 2), дети убеждают ся, что результат не изменится, если сначала найти сумму пер вого и второго слагаемых и прибавить к ней третье слагаемое или сначала найти сумму второго и третьего слагаемых, а затем прибавить эту сумму к первому слагаемому.

Детей подводят к практическому правилу о том, что можно группировать слагаемые так, как удобно для вычислений: 1 + 50 + 40 + 9 = 50 + 40 + 9 + 1 = (50 + + 40) + (9 + 1) = 90 + 10 = 100. Для усвоения этого вывода далее следует система тически включать в устные упражнения задания № 3 (с. 45), № 1 (с. 46), № 1 (с. 47) и т. п., в которых надо выбирать наи более удобный способ нахождения значения выражения.

Перейдём к рассмотрению геометрического материала. Как и прежде, в уроки включаются упражнения на различение геометрических фигур: прямая и кривая линии, от резок прямой, замкнутая и незамкнутая ломаные, различные многоугольники (с. 28, 30, 39 и др.). Есть задания на измерение и построение отрезков, сравнение отрезков на глаз и измерение м. Геометрические фигуры используются для развития у детей приёмов сравнения (с. 38), классификации (с. 39), обобщения (с. 44).

Методика работы над этими упражнениями известна учителю.

Новой является тема «Длина ломаной». Важно, чтобы к этом у уроку дети имели циркули, так как вводятся два способа нах ождения длины ломаной (с. 32). Первый способ — измерить каждое звено и полученные длины сложить. Второй способ — отложить с помощью циркуля на прямой последовательно отрезк и, равные по длине звеньям ломаной, а затем измерить получ ившийся отрезок. Оба эти способа закрепляются в дальнейшем, а также используются при нахождении периметра многоугольник а (с. 42, № 1 и др.). Здесь также важно, чтобы учащиеся упражнялись не только в сложении длин отрезков, но и в сложении отрезков, которые являются сторонами много угольников.

Постепенно усложняются задания на выделение треугольник ов и четырёхугольников, которые являются частями других мно гоугольников. Так, в задании «Какой фигуры не хватает?» (с. 45) надо увидеть, что квадрат («корпус лодки») составляется из двух заданных треугольников (не хватает треугольника — «паруса лод ки»). В аналогичном задании на с. 54 не хватает уже двух треугольников: одного маленького, дополняющего четырёхугольник — часть «крыши дома», а другого — большого, тако го, как заданные три треугольника, так как «домик» составляет ся из четырёх частей. Безусловно, ученик сможет правильно вы полнить эти задания сам, если начертит заданные части на клетч атой бумаге, вырежет их и практически сложит фигуру по обр азцу (это можно предложить в качестве домашней работы).

Таким же поисковым упражнением является задание № 3 (с. 51) («Как дополнить данный четырёхугольник до треугольник а?»). Только начертив данный четырёхугольник на клетчатой бу маге («Поставьте точку в уголке клетки, отсчитайте 6 клеток вниз и 2 клетки влево — поставьте вторую точку; от неё отсчит айте 2 клетки влево и поставьте третью точку» и т. д.), прик ладывая линейку то к одной стороне четырёхугольника, то к дру гой, ученики найдут разные способы преобразования этого четырёхугольника в треугольник.

Рассмотрим кратко изучение темы «Единицы времени.

Час. Минута».

Время — одна из самых трудных для изучения величин. Перв ые представления о времени у детей формируются ещё в до школьный период и опираются на доступные наблюдения после довательности событий во времени: ежедневные режимные мом енты, наблюдения за природными явлениями, за событиями в сказках и т. п. Однако восприятие времени достаточно субъек тивно, поэтому и в начале школьного обучения дети испытыва ют трудности при сравнении временных промежутков (что длитс я по времени короче, что дольше), а также с трудом устанавл ивают последовательность событий (что было раньше, что позж е, что за чем следует), особенно в тех случаях, когда подобных наблюдений не было в опыте ребёнка или при установлении этих отношений отсутствует опора на наглядную модель.

В 1 классе дети познакомились с единицей времени — час ом. Предполагается, что они научились определять время по часам с точностью до часа. Но многие дети к началу второго года обучения утрачивают эти знания и умения. Поэтому на подготовительном этапе в первой четверти полезно предлагать детям упражнения на установление временных отношений (раньше—позже, старше— моложе, что за чем следует во вре мени). За три-четыре урока до начала работы над темой следу ет предлагать детям следующие задания с использованием ци ферблата:

— Какое время показывают часы, если часовая стрелка указывает на число 9, а минутная стрелка — на число 12? (Ученики показывают на циферблате.)

— На часах ровно 12 часов (11 часов, 6 часов). Пока- жите, как располагаются стрелки на циферблате.

В этом случае при ознакомлении с минутой как новой единицей времени дети быстрее поймут, что все часы устроены так: большая (минутная) стрелка проходит расстояние от одной ма ленькой чёрточки до другой за 1 мин, а маленькая (часовая) стрелка проходит расстояние от одной большой чёрточки до друг ой за 1 ч (показывается на циферблате).

Новым на данном уро ке будет установление отношения: «В 1 часе — 60 минут». Надо показать, что за то время, когда маленькая стрелка сделает один шаг (1 ч), большая сделает полный оборот (сосчитать вместе с детьми: 5 минут да 5 минут будет 10 минут; 10 минут да 5 минут будет 15 минут да ещё 5 минут, будет 20 минут и т. д.), пройдёт 60 минут.

Чтобы дети почувствовали длительность минуты, обычно предл агают выполнить какие-нибудь практические операции в этот временной интервал, например узнать, сколько можно решить примеров или записать чисел за 1 мин. Затем можно разобрать пословицу «Минута час бережёт». После этого засекают время, которое требуется для решения задачи или примеров (с. 31). Анал огичное задание дают на дом. В дальнейшем предлагаются уп ражнения на закрепление знания единиц времени (решение за дач, задания на сравнение двух значений времени и др.). Особое внимание уделяют формированию умения называть и показывать время на модели часов (с. 31, № 2; с. 35, № 8; с. 45, № 7).

Подчеркнём ещё раз, что все материалы, данные в рубрике «Проверим себя и оценим свои достижения», предназначаются для самоконтроля и самооценки учащихся. Это относится и к рубрике на с. 94, 95. Ученик выбирает один из предложенных вариантов и в случае успешного выполнения варианта повышенного уровня сложности базовый вариант не выполняет.

В конце первой четверти предлагается ряд небольших тема тических самостоятельных работ, в которых можно решить, нап ример, 6 примеров в одно действие и 3 примера в два дейст вия (табличные случаи сложения и вычитания, а также нумерац ионные случаи); в другой раз можно дать только задачи: одну составную и две простые, например, на нахождение уменьшае мого (вычитаемого) с готовыми краткими записями и задачу на разностное сравнение (на отрезках); наконец, можно дать само стоятельную работу, в которую войдут задания на сравнение выр ажений, построение ломаной и нахождение её длины.

ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА ЗА ПЕРВУЮ ЧЕТВЕРТЬ

1. Арифметический диктант.

1)   Найди разность чисел 11 и 9.

2)   Найди сумму чисел 9 и 8.

3)   Увеличь 10 на 7.

4)   Уменьши 16 на 10.

5)   Запиши, на сколько 8 меньше, чем 13.

6)   Запиши, на сколько миллиметров 1 см больше, чем 1 мм.

2.    Реши примеры.

3.    Сравни выражения.

9 + 7 * 9 + 8                                                       14 – 9 * 13 – 9

4.  Реши задачу.

лось в классе?                                              плащей осталось в ателье?

5.  В качестве дополнительного задания для желающих мож но предложить следующее:

Поставь скобки так, чтобы равенство было верным:

15 – 10 – 4 = 9, 13 – 5 + 2 = 6. Или:

Начерти ломаную из трёх звеньев разной длины, зная, что длина ломаной равна 10 см.

Сложение и вычитание (продолжение)

В содержание работы на этом этапе включены устные приёмы сложения и вычитания в пределах 100. Продолжается работа над простыми и составными задачами, рассмотренными ранее, а так же над задачами новых видов. Вводятся буквенные выражения вида 8 + с, k – 7, а также уравнения вида х + 7 = 10, х – 5 = 6, 12 – х = 7, которые до конца года решаются подбором. Изучаются связи между результатами и компонентами сложения и вычитания, которые на данном этапе применяются для проверки правильности вычис лений. Хорошее знание этих связей позволит в дальнейшем (3 класс) успешно решать уравнения. Продолжается раб ота над геометрическим материалом, введённым на предыдущем этапе (преобразования геометрических фигур, нахождение длины ломаной линии и периметра многоугольника).

К концу первого полугодия учащиеся:

•         овладеют приёмами устных вычислений, научатся правильно выполнять сложение и вычитание чисел в пределах 100 (кроме случаев вида 45 + 23, 57 – 26, 37 + 48, 52 – 24), к которым применяются письменные приёмы вычислений (рассматриваются в третьей четверти);

•         научатся читать и записывать числовые выражения (со скобкам и и без них), находить их значения; усвоят понятие буквенн ое выражение, научатся читать, записывать и находить знач ения буквенных выражений при заданных значениях входящих в них букв;

•         усвоят понятие уравнение, научатся читать, записывать и решать уравнения подбором такого числа, при котором уравне ние превращается в верное равенство;

•         усвоят связи между результатами и компонентами сложения и вычитания, опираясь на них, установят способы проверки пра вильности выполнения этих действий и научатся применять спо собы проверки при вычислениях.

Наглядные пособия и дидактический материал

Для овладения приёмами вычислений потребуются демон страционные и индивидуальные пособия, с помощью кото рых можно изображать десятки и единицы: пучки — де сятки палочек и отдельные палочки или их рисунки. Мож но использовать треугольники — десятки кружков и карт очки с отдельными кружками (см. рис. на с. 53 настоя щего пособия).

1.       Для обучения решению задач полезно иметь иллюстративн ый материал к отдельным видам задач: краткие записи, чертежи, верно и неверно выполненные решения и т. п. (с. 57—93). Для индивидуальной работы удобно иметь карт очки с математическими заданиями.

2.       Для введения понятий буквенного выражения и уравнения целесообразно иметь демонстрационное наборное полотно с прорезями, чтобы вставлять подвижную ленту с набором чисел (с. 76, 79).

Рассмотрим работу над устными приёмами сложения и выч итания.

На первом уроке по теме (с. 57) проводится подготовительная работа к введению приёмов вычислений с дву-значными числами: повторяются переместительное и сочетательное свойства сложения (№ 2, первый столбик), эти свойства применяются при вычислен ии суммы удобным способом (№ 1); дети упражняются в замене двузначных чисел суммой разрядных слагаемых (№ 5). Часть этих заданий выполняется устно, часть — с записью в тетрадях. В устн ые упражнения можно включить для повторения десятичного сос тава чисел случаи вида 60 + 8, 96 – 6, 39 – 30, а также сложение и вычитание круглых десятков (40 + 30, 80 – 60). Аналогичные задания необходимо предлагать и на нескольких следующих уроках.

Как известно, последовательность изучения отдельных случа ев сложения и вычитания может быть различна, но традицион но учитывается прежде всего сложность вычислительных приёмов: сначала рассматривают приёмы, которые включают меньш ее число операций, затем приёмы, включающие большее числ о операций. Например, в сложении: сначала 36 + 2, затем 26 + 4, позже 26 + 7, аналогично в вычитании.

Там, где возможно, приёмы рассматриваются в сравнении: 36 + 2 и 36 + 20; приёмы сложения чередуются с аналогичными приёмами вычитания, которые вводятся в сопоставлении с рассмотренными только что приёмами сложения. Таким образ ом обеспечивается определённый перенос и дифференциация: 36 + 2, 36 + 20 (с. 58) и 36 – 2, 36 – 20 (с. 59); 26 + 4 (с. 60) и 30 – 7 (с. 61); 60 – 24 (с. 62); 26 + 7 (с. 66) и 35 – 7 (с. 67). В хорош о подготовленном классе соответствующие приёмы сложения и вычитания можно вводить одновременно так называемыми укруп нёнными дидактическими единицами.

Приёмы вводятся довольно интенсивно в начале второй чет верти, а затем закрепляются на большом промежутке времени — до конца декабря и далее, до конца учебного года. Это объясн яется тем, что ученик должен не только освоить систему опер аций, составляющих каждый приём («алгоритм выполнения действия»), но и научиться выбирать приём применительно к данным числам («алгоритм распознавания»). Каждый учитель сталкивался с таким фактом: дети поняли отдельный конкретный приём, научились решать аналогичные примеры, но после ознакомления со следующими приёмами начинают смешивать приёмы и допускать ошибки. Вспомним, что такое же явление наблюдается и при изучении таблиц сложения (таблиц умножения, склонений существительных и т. п.): пока изучается каждый вопрос в от дельности, всё обстоит благополучно, но как только изучена те ма в целом, начинаются трудности и ошибки. Поэтому настоящ ее закрепление умений и формирование навыков происходит тогда, когда приходится решать разные примеры и выбирать из ряда способов действий соответствующий и самый удобный.

Методика работы, направленная на овладение детьми приёмам и вычислений, известна учителю. Вначале приём (способ дей ствия) раскрывается с помощью соответствующего предметного действия (например, с пучками палочек и отдельными палочкам и или другими моделями десятков и единиц). Затем с опорой на иллюстрации дети решают пару примеров с подробной запис ью и устным пояснением, а после этого пару примеров с краткой записью и устным пояснением (обычно на первом уроке больше сделать не удаётся). На основе сравнения всех решённых прим еров делается обобщение, как решать подобные примеры: единицы складывают с единицами, десятки — с десятками (с. 58). На следующем уроке для закрепления решают примеры с по дробным и кратким пояснением приёма и повторяют вывод. По этому аналогичные приёмы вычитания дети «открывают» с больш ой долей самостоятельности. Решив с опорой на предметные действия или иллюстрации пару новых примеров с объяснением вслух и сопоставив их с только что решёнными примерами на сложение, дети без особых затруднений формулируют вывод: единицы вычитают из единиц, десятки — из десятков (с. 59). Затем переходят к решению примеров на сложение и вычитание, сравнивая приёмы вычислений: 54 + 3, 54 – 3, 76 – 20, 76 + 20.

Так как приходится прибавлять к одному из слагаемых, то, чтобы дети не забыли другое слагаемое, разрядные числа, сос тавляющие двузначное число, рекомендуют подписывать под ним в следующей строке, соединяя числа проведёнными от руки отр езками («лучиками», «ножками» и т. п. — с. 58—59). Некот орые учителя говорят: «С записью чисел-помощников» — и со ветуют детям (особенно тем, кто нуждается в этом) не только записывать разрядные числа, но и точкой отмечать то число, к которому прибавляют (из которого вычитают) в этом примере второе число.

В классе, где особенно много слабо подготовленных детей, на этапе овладения приёмами вычислений некоторые методисты рекомендуют использовать как записи, так и модели десятков и единиц:

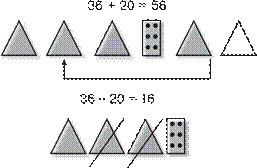
Отметим, что на таких рисунках не следует использовать зна ки арифметических действий.

Вычислительный приём для случаев вида 26 + 4 (с. 60) включ ает сложение не только единиц, но и десятков. Рассматривая подробную запись, данную под примером, дети видят, что вначал е складывают единицы, а затем полученный десяток прибавл яют к десяткам. Выполняя краткую запись, можно объяснять короче.

Например, решая пример 81 + 9, говорят: 81 — это 80 и 1 (пишут под числом), к 1 прибавить 9, получится 10, 80 и 10 — это 90.

Сложение (вычитание) круглых десятков не надо объяснять вслух, так как у детей уже сформировался навык подобных вы числений (т. е. эти действия выполняются в уме). Только в случ ае ошибки приходится объяснять даже давно изученный приём подробно и вслух.

Для того чтобы у детей не произошло неверного обобщения (суммой заменяют всегда первое число), в данный урок в учеб нике предлагается включить несколько примеров вида 60 + 18, 20 + 14, где второе число заменяют разрядными числами, и, значит, удобнее сначала сложить десятки, а затем прибавить едини цы. Решение таких примеров, кроме того, подготавливает детей к рассмотрению приёма вычитания вида 60 – 24.

Чтобы подготовить детей к овладению приёмом для случаев вида 30 – 7, надо использовать специальные упражнения на замену чисел — круглых десятков суммой по образцу: 50 = 40 + , 70 =  + 10 (с. 59, № 5; с. 61, № 1).

В приме рах вида 30 – 7 отсутствуют отдельные единицы. Но если дать детям в руки связанные в десятки палочки и спросить, как из 3 десятков вычесть 7 единиц, некоторые дети догадываются раз вязать 1 десяток и взять из него 7 палочек. Выполнив подробн ую запись этого приёма, дети должны отметить, что и здесь еди ницы вычитают из единиц — из 10 единиц, которые получают, заменяя уменьшаемое суммой чисел, одно из которых равно 10.

Особое внимание надо обратить на вычитание нескольких еди ниц из 100. Например, 100 – 4. Объяснение: 100 — это 90 и 10 (пишут под примером); вычитаем 4 из 10, получится 6; 90 да 6 получится 96.

Новый приём полезно на этом же уроке сопоставить с рассмотренными ранее приёмами: 76 + 4 и 80 – 4, 48 – 6 и 40 – 6, чтобы дети осознали его особенности.

Приём вычислений для случаев вида 60 – 24 достаточно сложн ый и требует особого внимания (с. 62). В отличие от предыдущ их приёмов, когда вычитали из одной части уменьшаемого и требовалось прибавить другую часть, в новом приёме надо вы честь обе части — и десятки, и единицы. Это хорошо видно де тям, когда они выполняют предметные действия, например на па лочках.

Заметим, что если используются модели чисел из треугольников и точек, то, изобразив уменьшаемое с помощью треугольников-десятков, надо на этом же рисунке зачеркнуть необходимое чис ло десятков, а в одном из оставшихся треугольников изобразить 10 точек и зачеркнуть из них необходимое число единиц.

На первом уроке полезно увеличить количество упражнений на основе предметных действий с подробным объяснением, а такж е рассмотреть примеры на сопоставление приёмов (30 + 12 и 30 – 12) и затем обобщить: прибавляем и вычитаем по част ям — сначала десятки, потом единицы.

На следующих трёх уроках рассматриваются новые виды зад ач (с. 63—65) и обязательно закрепляются изученные приёмы вычислений, особенно приёмы вычитания, которые необходимо давать в сопоставлении. Например: 40 – 6 и 40 – 26, 67 – 30 и 60 – 37. Решать эти примеры полезно с подробным пояснением.

Последними вводятся устные приёмы сложения и вычитания с переходом через десяток вида 26 + 7 (с. 66) и 35 – 7 (с. 67). Сами приёмы известны детям — это прибавление и вычитание по частям так, чтобы после первого шага получились круглые десятки: 26 + 4 + 3, 35 – 5 – 2. В устные упражнения полезно включать задания на повторение состава однозначных чисел, а также на дополнение данных чисел до круглого числа. Например, дополни до 30 числа 24, 26, 27, 28.

Некоторые дети, хорошо знающие таблицу сложения, иногда предлагают другой приём: 26 + 7 = 20 + (6 + 7) = = 20 + 13 = 33. Разумеется, не следует запрещать им вычислять таким образом. Однако вводить сразу два приёма для всех учащихся на данном этапе нецелесообразно. Наблюдения показывают, что, познако мившись с приёмом вычитания с переходом через десяток, мно гие дети делают неверный перенос этого приёма на новые случаи (35 – 7 = = 30 + (7 – 5) = 30 + 2 = 32).

Приём, включающий пол учение круглого десятка (прибавление и вычитание по частям), как более известный детям осваивается ими без особых затруд нений и, кроме того, способствует закреп-лению табличного слож ения и вычитания.

Во все уроки, отведённые на изучение устных приёмов слож ения и вычитания, включаются числовые выражения, содержащ ие два действия (со скобками и без них). Эти упражнения пред назначены не только для отработки вычислительных навыков, но и для закрепления умений читать и записывать выражения, для применения правил порядка выполнения действий в выражениях.

В тех случаях, когда выражения содержат действия над двузнач ными числами с использованием изученных приёмов вычислений (с. 63, 64 и т. д.), опытные учителя советуют детям записывать промежуточный результат над соответствующим знаком действия, так как многие дети, переходя ко второму действию, забывают полученный результат первого действия. Запись этого числа предупреждает многие ошибки: в частности, помогает детям в вы боре приёма вычисления.

Этот же факт — необходимость зрит ельного восприятия чисел — надо учитывать при проведении устн ых упражнений (устного счёта).

Дети только осваивают вычис лительные приёмы, у них начинает складываться умение выполнять те операции, которые входят в вычислительный приём, а выбор приёма представляет определённые трудности. Поэтому для устных вычислений надо предлагать примеры либо данные в учебни ке, либо записанные на доске. Для того чтобы поддерживать у детей интерес к вычислениям, предлагают примеры с пропущенны ми знаками действий, задания на сравнение выражений, проверку заданных равенств и неравенств, таблицы (например, № 21 на с. 74), а также игры: круговые примеры, примеры с шифром, занимательные рамки, магические квадраты и т. п.

На уроках закрепления (с. 72—75) можно предложить детям самостоятельную работу, включающую 8—10 примеров на все рассмотренные случаи сложения и вычитания, с целью выявлен ия тех приёмов, которые недостаточно освоены, чтобы уделить им больше внимания на следующих уроках. Разумеется, в тече ние трёх недель у детей не будут сформированы навыки вычис лений, поэтому не следует включать эти случаи в арифметический диктант. Примеры в одно действие дети должны записать в тетрадях (с доски или из учебника) и решать их в своём темп е. Можно также разрешить детям использовать дополнительные запи си, если это поможет им при вычислениях.

При ознакомлении с буквенными выражениями и уравнения ми (с. 76—83) используются в основном табличные случаи сло жения и вычитания и наиболее лёгкие случаи сложения и вычи тания в пределах 100, что вполне закономерно. Поэтому приме ры на закрепление вычислительных навыков учитель подбирает сам, учитывая результаты самостоятельных работ в своём класс е. Напомним ещё раз, что целесообразно включать приёмы выч ислений в сопоставлении. Например: 72 + 5, 72 + 8, 72 + 9; 46 + 8, 46 – 8; 57 – 20, 50 – 27 и т. п.

Далее рассматриваются способы проверки сложения и выч итания (с. 84—87). Логика построения уроков такая: сначала на трёх-четырёх примерах рассматривают связь между результа том и компонентами каждого из этих действий. Для этого к данному примеру составляют обратные примеры. Их предлагают читать с названиями чисел так, как они назывались в первом примере:

40 + 20 = 60

60 – 20 = 40

60 – 40 = 20

Из суммы 60 вычли второе слагаемое 20, получили первое слагаемое 40 (третий пример — аналогично).

После того как сделано 3—4 таких конкретных вывода, дети сами смогут обобщить их и сформулировать или прочитать по учебнику вывод: если из суммы двух слагаемых вычесть одно из слагаемых, то получится другое слагаемое (с. 84).

Для введения способа проверки вычитания достаточно расс мотреть одну связь, а именно что получается, если сложить разность и вычитаемое (с. 86, 87). Например:

28 – 6 = 22

22 + 6 = 28

К разности 22 прибавили вычитаемое 6, получили уменьшае мое 28.

На основе этих выводов раскрываются способы проверки вып олненных действий. Важно, чтобы дети усвоили способ провер ки в полной формулировке так, как дано в учебнике: не только называли действие, с помощью которого выполняется проверка, но и указывали, с какими числами эти действия надо выполнять, и обязательно отмечали, в каком случае считают вычисления прав ильными (если получится другое слагаемое..., если получится уменьшаемое...), а в каком — неправильными (если не получится..., значит, в вычислениях допущена ошибка).

Чтобы дети усвоили способы проверки и пользовались ими правильно, надо включать задания не только вида «решить и пров ерить», но и вида «проверить решённые примеры». Тогда учащ иеся убеждаются в том, что надо не только выполнить дейст вие над результатом и компонентом, но и сравнить полученное число с имеющимся в примере (увидеть, что они не всегда сов падают). Вот примерные упражнения:

Проверьте, правильно ли решены примеры: 50 + 24 = 74      50 – 24 = 34        32 + 60 = 90 80 – 7 = 83 43 + 7 = 50         28 + 3 = 58

Для предупреждения формального подхода к проверке вычисл ений можно предлагать такие задания:

— Рассмотрите примеры и объясните, почему проверка  не по могла найти ошибку в вычислениях:

60 – 27 = 47                               54 + 6 = 50                           87 – 5 = 37

47 + 27 = 60                               50 – 6 = 54                           37 + 5 = 87

Образцы такой проверки можно найти в тетрадях своих уче ников. Целесообразно привлекать этих же учеников к работе над ошибками, однако называть «автора» в подобных ситуациях не следует, соблюдая известное положение педагогики: «Ученик имее т право на ошибку».

Рассмотрим работу над задачами.

Во второй четверти продолжается работа над задачами на на хождение неизвестного слагаемого, уменьшаемого, вычитаемого. Дети не только составляют и решают эти задачи, но также учатс я проверять простые задачи на нахождение суммы и остатка и обратные им, составляя и решая обратные задачи (с. 57, № 6; с. 64, № 4 и др.).

Заслуживают внимания простые задачи на нахождение суммы, в которых есть выражение «столько..., сколько...» (с. 63, № 1). Это подготовительные задачи к составным задачам (с. 73, № 9). Решение этих задач не представляет трудности для детей, ошибк и иногда возникают при формулировке ответа. Слабо подготовл енные дети могут нарисовать схемы к задачам с небольшими числами. Например: «Нарисуйте в одной строчке 3 квадрата и 2 треугольника, а в другой — столько кружков, сколько квад ратов и треугольников вместе. Сколько кружков вы нарисовали и почему?» Так же можно проиллюстрировать задачу № 2 (с. 63), а можно решить её с опорой на чертёж, который сдела ет учитель в процессе беседы с детьми:

— Обозначим отрезком, сколько красных квадратов  вырезал а Даша (чертит отрезок произвольной длины на доске и делает надпись: 7 кв. — это красные квадраты).

— Прочитайте, сколько было голубых квадратов, и ска- жите: их было больше или меньше, чем красных? Значит, второй от резок начертим меньше, чем первый (продолжает первый отре зок и делает надпись: 4 кв.).

— Начертим ниже отрезок, который будет изображать  зелёные квадраты. Что вы знаете про них? Каким должен быть ниж ний отрезок? Почему?

Заметим, что и в схеме, и на чертеже искомое число надо изображать отдельно, для того чтобы показать отношение равенства (столько же, такой же длины и т. п.). Подчёркивая осо бенности этих задач, можно привести похожую задачу, в которой отсутствует отношение равенства. Например: «Таня, Юра и Све та решали примеры. Таня решила 4 примера, Юра — 3. Сколь ко примеров решила Света?» После того как дети установят, что решить эту задачу нельзя, им предлагается дополнить условие так, чтобы можно было ответить на вопрос задачи.

Новыми в определённой мере являются простые, а также сос тавные задачи, связанные с движением (с. 64—65). Решая их, дети начинают осознавать такие понятия, как «расстояние» и «пройденный путь», их связь (расстояние можно узнать через пройденный путь). Вначале некоторые дети не понимают такие задачи и воспринимают их, скорее, как задачи-шутки, где вопрос не соответствует условию: «Две девочки идут с концов моста (аллеи, дорожки). Одна прошла столько-то метров (шагов), друг ая — столько-то». Вопрос задачи: «Какова длина моста (аллеи, дорожки)?» Дети без труда отвечают, сколько метров (шагов) прошли эти девочки вместе, но часть учащихся не соотносят этот ответ с вопросом задачи. Понять, что, определив пройденный путь, мы узнаем и расстояние между двумя точками, откуда нач алось движение, помогут не только чертежи, но и наблюдения за реально движущимися объектами (детьми, машинками, подвижн ыми моделями).

Важно обратить внимание детей на направление движения — в одном направлении, в разных (в том числе навстречу друг друг у). Эти слова и термины усваиваются лучше всего в реальной обстановке (на экскурсии, на прогулке), когда дети сами «моде лируют» соответствующие ситуации. Хотя основная работа над этими понятиями предстоит в 3—4 классах, здесь полезно пров ести некоторые наблюдения, а также отметить особенности чертежей: направления движения обозначают стрелками, место встречи — флажком, пройденный путь и расстояние —  отрез ками.

При работе над составными задачами продолжают сравнивать простую и составную задачи (с. 62, № 5). Например, детям пред лагается придумать вопрос к данному условию (с. 61, № 5). Пусть они поставят и такой вопрос, чтобы задача решалась двумя дей ствиями, и такой, чтобы задача решалась одним действием. Это поможет им в составлении плана решения составной задачи.

Эффективным упражнением на различение простой и со ставной задач является задание на выбор решения к данным задачам (с. 63, № 3). Чтобы выбор не был случайным, надо про читать обе задачи, сравнить их условия, вопросы, а затем пред ложить объяснить, что узнают при выполнении действий в каж дом выражении.

Задания на пояснение смысла составленных выражений встре чаются довольно часто (с. 66, № 3; с. 68, № 4; с. 69, № 4 и др.). Предложенные в учебнике выражения полезно дополнять другими, в том числе такими, которые не соответствуют данном у условию. Например, к задаче № 3 (с. 66) можно дополнит ельно дать выражения: 15 – 5, 40 – 15 – 5, 40 + 15. Пусть дет и объяснят, что можно узнать, выполнив указанные действия, и почему считают, что последнее выражение нельзя составить по данному условию.

Полезно обратное задание: на какие вопросы можно ответить, опираясь на данное условие, и какие действия надо выполнить, чтобы ответить на эти вопросы (соответствующие выражения зап исывают)? Например, по условию задачи № 3 (с. 68) дети со ставляют следующие вопросы:

— На сколько больше было девочек, чем мальчиков?  (На 6 – 4.)

— Сколько всего девочек и мальчиков было сначала в  чи тальном зале? (6 + 4.)

— Сколько детей стало после того, как пришли ещё 

8 уче ников? ((6 + 4) + 8.)

— Сколько всего стало бы мальчиков, если все пришед- шие 8 были мальчики? (4 + 8.)

— Сколько всего стало бы девочек, если все пришед- шие 8 были девочки? (6 + 8.)

Во второй четверти уделяют достаточное внимание обучению решению задач разными способами. Ранее дети выполняли подготовительные упражнения — рассматривали готовые решен ия и объясняли, что узнавали каждым действием. Затем в учебник включались задания с указанием: «Реши задачу разными способами». Каждый раз пол езно выяснять, что это значит — решить разными способами.

Рассмотрим работу над задачей № 3 (с. 62). Опираясь на её краткую запись и представляя описанную ситуацию, дети под рук оводством учителя составляют план и записывают решение: (20 + 15) – 5 (вычисляют значение выражения, подчёркивают ответ). Объясняют: сначала узнали, сколько вёдер воды было в двух бочках вместе, а потом сколько вёдер воды осталось. Далее учитель предлагает: «Представьте, что воду для поливки цветов брали только из первой бочки. Что можно узнать по так им данным: в бочке 20 вёдер воды, 5 вёдер воды взяли? Теперь вы знаете, сколько вёдер воды осталось в первой бочке и скольк о — во второй. Что можно узнать?» Запись решения: (20 – 5) + 15 (вычисляют значение выражения, подчёркивают ответ). Зат ем учитель предлагает рассмотреть другую ситуацию: 5 вёдер для поливки цветов брали из второй бочки. Какое выражение тогда можно составить по задаче? Запись: 20 + (15 – 5) или (15 – 5) + 20. Оба выражения справедливы, так как первым действ ием узнают, сколько вёдер воды осталось во второй бочке, а вторым — сколько всего вёдер воды осталось в двух бочках.

Вычислив значения выражений и сравнив результаты, дети убеждаются в том, что ответ задачи везде одинаковый, хотя расс уждали по-разному и действия. Для закрепления умения можно предложить составить по кратк ой записи вторую задачу из № 5 (с. 62) и решить её разными способами.

Ко второй задаче из № 3 (с. 62) можно составить два разн ых выражения: 12 – 5 – 2 и 12 – (5 + 2). Рассмотреть эту зад ачу, вероятно, придётся на одном из следующих уроков. Важно, чтобы дети усвоили суть: решая задачу разными способами, при составлении плана решения рассуждают по-разному (ставят разные вопросы, решают задачу разными действиями, но ответ получают одинаковый). Чтобы дети не сводили решение разным и способами к манипулированию числами, полезно предложить верное и неверное решение. Например, к последней задаче мож но дать выражение 12 – 5 + 2. Пусть дети убедятся в том, что по данной задаче невозможно объяснить, что узнавали каждым действием в этом выражении, и ответ получается другой — зна чит, это неверный способ решения задачи.

Умение решать задачи разными способами, особенно самостоя тельно искать и находить разные пути решения, — сложное умение, формируется оно как в начальной, так и в средней школе в течение многих лет и не только на уроках математики. Способность увидеть отличные от обычных связи и, опираясь на них, выйти на другой ход решения задачи — это один из эле ментов творчества, и не следует ожидать, что за короткое врем я дети добьются больших успехов в творческом развитии. Во второй четверти эта работа только начинается и, естественно, проходит под руководством учителя. С расчётом на длительное время в учебнике подобраны специальные задачи и даётся указ ание: «Решите задачу разными способами». Хотя задание звуч ит одинаково, методика работы должна постепенно меняться, а именно: ученику должно предоставляться всё больше самостоятельности при поиске способов решения.

Для усвоения содержания задачи (после того как дети прочит али её про себя и вслух) используют либо краткую запись, либ о чертёж. Чертёж хорошо помогает при решении задач, котор ые включают увеличение (уменьшение) числа на несколько еди ниц (с. 57, № 3; с. 74, № 16; с. 93, № 29 и др.). Многие дет и смогут решить задачи на смекалку (с. 61—62 и далее), если им подсказать, что к задаче надо сделать чертёж. Опираясь на чертёж, дети быстрее догадываются, как решить задачу разными способами (с. 67, № 4; с. 69, № 4; с. 82, № 3 и др.). Если чертёж сделан на доске, то после решения задачи можно изме нить числа (несколько или все) и предложить детям составить по чертежу новую задачу. Несмотря на то что во второй четверти часто использовались чертежи при работе над задачами, многие дети ещё не могут сами сделать чертёж к задаче, поэтому его выполняет учитель на доске в процессе беседы с детьми, либо они рассматривают готовый чертёж по учебнику.

В период закрепления устных приёмов сложения и вычитания (с. 68—75) можно предложить тематическую работу, в которую включить одну простую задачу — на нахождение уменьшаемого, вычитаемого или слагаемого. Например: «Когда на полку поста вили (с полки сняли) 5 книг, там стало 20 книг. Сколько книг было на полке сначала?» Другая задача — составная, включаю щая увеличение (уменьшение) числа на несколько единиц и нахождение суммы. Например: «На стоянке было 10 легковых ма шин, а грузовых — на 4 меньше (больше), чем легковых. Сколь ко всего машин было на стоянке?» Решение задачи ученики мог ут записать так, как им удобно, — по действиям или в виде выражения. Желательно сформулировать полный ответ задачи.

В конце второй четверти даётся понятие об уравнении. Что бы дети правильно усвоили понятие, надо провести серьёзную подготовку. С одной стороны, они должны накопить опыт рабо ты с равенствами, усвоить, что записи со знаком «=» (равенств а) могут быть верными и неверными. Таких упражнений начи ная с 1 класса учащиеся выполняли много: проверяли, являются ли данные равенства верными или неверными; составляли верные равенства из заданных выражений; вставля ли пропущенные знаки действий или знаки сравнения так, что бы получились верные равенства и неравенства, и т. п. С другой стороны, нужен определённый опыт работы с переменной. С так ими упражнениями дети также сталкивались. Это прежде всего примеры с пропущенными числами (6 +  = 9,  – 4 = 6). Важно, чтобы они решались подбором. Для этого в окошко вставл яют друг за другом не одно, а несколько чисел, и дети объясн яют, почему некоторые числа не подходят, так как получаются неверные равенства, а одно число подходит, так как получается верное равенство (с. 78, № 6). Заметим, что особенно полезны ми в этом плане являются неравенства с пропущенными числам и, где подбор не ограничивается одним числом, а подходит не сколько чисел. Например:  < 3, 4 + 1 > ,  – 7 < 4 и т. п.

Для того чтобы дети приобрели некоторый опыт работы с переменной (этот термин не вводится), перед введением уравнения даётся понятие о буквенных выражениях (с. 76—79). Методика введения таких выражений (пока с одной переменной) раскрыта в учебнике. Детям предлагаются простейшие выражен ия — сумма или разность чисел, одно из которых обозначено окошком:  + 4, 10 –  и т. п. В окошки следует подставлять различные числа, т. е. получать числовые выражения и находить их значения. Затем объясняется, что вместо квадрата (окошка) в математике используют латинские буквы. Дети учатся читать и записывать буквенные выражения, находить их значения при за данных значениях букв (с. 77, № 2). Запись:

                       k + 7                                                   k – 7

                         10 + 7 = 17                                       10 – 7 = 3

                         7 + 7 = 14                                          7 – 7 = 0

Вначале учащиеся подставляют вместо буквы только те чис ла, которые даны в задании, и выполняют вычисления устно или письменно (как показано выше или в таблице № 1 на с. 78).

По этим записям дети без особых затруднений объясняют, поч ему получаются разные значения буквенного выражения, почем у они увеличиваются или уменьшаются. Позднее (во втором пол угодии и в 3—4 классах) детям предлагают самим придавать значения входящим в выражение буквам и находить значения пол ученных числовых выражений. При этом выясняют, какие значения можно придавать буквам, почему не подходят те или иные значения уменьшаемого или вычитаемого, при каком значении буквы получается самое маленькое значение выражения, можно ли назвать самое большое значение выражения и т. п.

Опираясь на сформированные умения различать верные и не верные равенства и подставлять вместо буквы различные её зна чения, знакомят детей с уравнением (с. 80). Уравнение — это равенство с неизвестным числом, которое надо найти. При нах ождении выполняют подстановку заданных чисел (с. 80, № 1) и убеждаются, что данное равенство может быть и неверным, и верным. Чтобы решить уравнение, надо найти только те значе ния неизвестного (если они существуют), при которых получается верное равенство (с. 82, № 1, п. 2). Важно, чтобы, подставив каждое из заданных чисел, дети не за меняли равенство неравенством, что часто наблюдается в прак тике (9 + 7 больше, чем 14, значит, 7 не подходит; 9 + 1 меньш е, чем 14, значит, 1 не подходит). Надо подставлять значение буквы в равенство и проверять, какое равенство получилось — верное или неверное (9 + 7 = 14 — это неверное равенство, так как 16 не равно 14, значит, неизвестное число не равно 7, а  9 + 5 = 14 — верное равенство, так как 14 равно 14, значит, неизвестное число равно 5).

На следующем уроке дети должны закрепить знания об уравн ении (например, снова прочитать текст на с. 80) и найти уравн ения среди различных записей (с. 82, № 1), объяснив, почему они считают, что последние два равенства являются уравнениям и, а остальные нет. Заметим, что на данном этапе пол езно читать уравнения в виде вопроса («Из какого числа надо вычесть 8, чтобы получилось 10?» и т. п.).

Даже составляя уравнения по таблице (с. 83, № 1), надо нах одить неизвестное подбором, так как именно в этом случае закрепляется правильное понятие об уравнении. Решение уравнений на основе знания связей между результатами и комп онентами будет рассматриваться в 3 классе после изучения связей и закрепления на способах проверки вычисле ний (с. 84—93).

На данном этапе в уравнениях используются в основном табличные и нумерационные случаи сложения и вычи тания, поэтому подбирать неизвестное число достаточно легко.

На уроках закрепления можно предлагать такие упражнения:

1.             Проверьте, правильно ли решены уравнения.х – 15 = 0                 у + 40 = 40           96 – х = 0 х = 15 у = 40    х = 0

2.             Запишите уравнения и решите их, подбирая неиз-вестное число.

1) К какому числу надо прибавить 9, чтобы получилось 17? 2) Какое число вычли из 87, если получили 80?

3. На какие группы можно разбить следующие уравнения?

12 – х = 12                       7 + у = 7                  18 + у = 19                 х – 1 = 0

Чтобы предупредить неверное обобщение учащихся о том, что уравнения всегда имеют только одно решение, иногда предлагаются уравнения, имеющие множество решений (например: х – х = 0). В этом случае при любом значении неизвестного получается верное равенство. С этой же целью полезно включать в уроки уравнения, которые не имеют решений на множестве целых неотрицательных чисел (например: 10 + x = 8, 15 – x = 20). Дети не могут пока найти ни одного значения неизвестного, чтобы получились верные равенства.

Работа над уравнениями только начинается в конце второй четверти, поэтому, естественно, уравнения и буквенные выраже ния не включаются в контрольные работы.

В итоговую контрольную работу за полугодие можно включ ить арифметический диктант (табличные и нумерационные случ аи сложения и вычитания), задачу в два действия, задания на сравнение выражений и нахождение длины ломаной, примеры на сложение и вычитание в пределах 100 (можно исключить случаи сложения и вычитания с переходом через десяток).

ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА

ЗА ПЕРВОЕ ПОЛУГОДИЕ

1. Арифметический диктант.

1)   Увеличь 20 на 10.

2)   Уменьши 76 на 6.

3)   Найди сумму чисел 50 и 40.

4)   Уменьшаемое — 70, вычитаемое — 50, найди разность.

5)   Узнай, на сколько 16 больше, чем 9.

6)   Запиши, сколько минут в одном часе.

7)   На сколько миллиметров 1 см больше, чем 1 мм?

8)   На сколько копеек 1 копейка меньше, чем 1 рубль?

9)   Запиши выражение и найди его значение:

                           а) к числу 60 прибавь разность чисел 40 и 10;

                          б) из числа 80 вычти сумму чисел 13 и 7.

2.    Реши задачу.

3.    Выпиши только верные равенства и неравенства¹.

¹

Задание оформляется так: 43 + 7 > 37 + 3

                                                                      50 > 40.

5. Дополнительное задание^[3].

Длина ломаной из трёх звеньев равна 12 см. Какой длины могут быть её звенья, если известно, что два из них имеют оди наковую длину? Начерти такие ломаные.

В учебнике (с. 94, 95) даны тексты разноуровневых контрольных работ. Если на уроках закрепления использовались подобные аналогичные задания работы, то для контрольной работы необходимо составить работы на отдельных листах для индивидуальной работы ученика.

ВТОРОЕ ПОЛУГОДИЕ

ЧИСЛА ОТ 1 ДО 100

Во втором полугодии выделяют 3 основные темы:

Сложение и вычитание (письменные вычисления) (23 ч)

Умножение и деление (39 ч)

Итоговое повторение. Контроль и учёт знаний (8—10 ч)

Раскрытие новых приёмов вычислений чередуется с ознаком лением детей с новыми геометрическими фигурами: прямой, остр ый и тупой углы, прямоугольник (квадрат); ученики узнают свойс тво противоположных сторон прямоугольника.

Сложение и вычитание (письменные вычисления)

По окончании работы над темой дети овладеют следующими знаниями, умениями и навыками:

•         твёрдо усвоят ранее изученные устные приёмы сложения и вычитания; особое внимание при этом должно быть уделено отработке автоматизированных навыков в отношении табличных случаев сложения и вычитания;

•         освоят письменные приёмы сложения и вычитания дву значных чисел с записью вычислений столбиком; научатся провер ять правильность выполнения сложения и вычитания, исполь зуя знание связи между компонентами и результатом каждого из этих арифметических действий;

•         научатся по-разному читать числовые выражения (9 + + 5 — сумма чисел 9 и 5, первое слагаемое — 9, второе — 5, найти сумму, увеличить 9 на 5; 12 – 4 — разность чисел 12 и 4, уменьшаемое — 12, вычитаемое — 4, найти разность, умень шить 12 на 4);

•         научатся решать текстовые задачи в одно и в два действия (простые и составные);

•         научатся решать задачи геометрического содержания: чер тить фигуры на клетчатой бумаге, выполнять упражнения по конструированию фигур (например, вычленять из данной фигуры составляющие её части, преобразовывать одну фигуру в другую и т. п.).

Наглядные пособия при изучении этой темы те же, что и при изучении материала, данного в первой части учебника для 2 класса.

Письменные приёмы сложения и вычитания включают следу ющие операции: правильную запись чисел в столбик (десятки под десятками, единицы под единицами), сложение или вычитание единиц, затем сложение или вычитание десятков, запись и фор мулировку ответа. В зависимости от данных чисел выполняются и другие операции: например, при сложении единиц в результат е может получиться двузначное число, из которого надо выдел ить десяток и прибавить его к десяткам, а при вычитании числ о единиц в уменьшаемом может быть меньше, чем в вычитае мом, тогда из числа десятков уменьшаемого «занимают» десяток и прибавляют 10 к единицам уменьшаемого, после чего выполн яют вычитание. Именно поэтому в учебнике рассматриваются различные случаи сложения и вычитания в зависимости от чис ла операций, составляющих приём.

Назовём эти случаи и поряд ок их следования в учебнике:

1) 45 + 23 (с. 4)                          5) 87 + 13 (с. 16) 2) 57 – 26 (с. 5)                                 6) 40 – 8 (с. 18)

3) 37 + 48 (с. 12)                        7) 50 – 24 (с. 19) 4) 37 + 53 (с. 13)                              8) 52 – 24 (с. 29)

Рассмотрим подробнее, как можно познакомить учащихся с приёмом письменного сложения для случаев вида 45 + 23 (сум ма единиц слагаемых меньше 10).

С целью подготовки к рассмотрению нового материала над о повторить:

— десятичный состав двузначных чисел, предложив де- тям уп ражнения вида: «Сколько десятков и единиц в числе 45? в чис ле 80?», «Назови число, в котором пять десятков и две едини цы», «В числе 46 четыре десятка. Сколько в нём единиц?»;

— приёмы сложения в случаях вида 37 + 40, 40 + 23,  37 + 2. Примеры можно записать на доске. Учитель называет пример, дети устно решают его, дают ответ, кратко поясняя ход решения (десятки прибавляют к десяткам, а единицы — к еди ницам). Поясняя решение примера 40 + + 23, ученики должны сказать, что число 23 прибавляли по частям: сначала 20, а потом ещё 3.

При ознакомлении с письменным приёмом сложения первого вида можно использовать запись и иллюстрацию, аналогичные данным в учебнике на с. 4. Здесь предложен удачный методичес кий приём ознакомления с письменным сложением: сначала учен ики находят результат, пользуясь известным им устным приёмом сложения, а затем переходят к письменному приёму, который отл ичается от устного только новой записью решения (столбиком) и порядком выполнения операций.

Учитель записывает на доске пример, аналогичный рассмотр енному в учебнике на с. 4, например: 54 + 32. Дети называют, сколько десятков и единиц в каждом слагаемом. Учитель изоб ражает данные числа на предметном абаке (см. рис. на с. 4) и предлагает устно вычислить сумму чисел 54 и 32. Дети объясняют: «Будем прибавлять 32 по частям: сначала 30, получится 84, и ещё 2, получится 86». Учитель записывает: 54 + 32 = (54 + 30) + 2 = 86.

— Сколько десятков было в первом слагаемом? во вто- ром? в полученной сумме? Сколько единиц было в первом слагаемом? во втором? в полученной сумме? Назовите ответ решённого при мера.

Учитель поясняет: «При сложении двузначных чисел удобнее записывать решение примеров по-другому — столбиком, тогда легче вычислить сумму: числа записывают одно под другим так, чтобы десятки были записаны под десятками, а единицы — под единицами. Слева от чисел ставится знак «+» и проводится черта под числами, ниже которой будет записываться сумма. Зап омните: письменное сложение начинается с единиц. Скажите, сколько единиц в первом слагаемом, во втором. Складываем единицы: 4 ед. + 2 ед. = 6 ед. Пишем 6 под единицами. Теперь складываем десятки: 5 дес. + 3 дес. = 8 дес. Пишем 8 под де сятками. Теперь можно прочитать, чему равна сумма». Объя снение сопровождается соответствующей записью столбиком на доске (с. 4). Учитель выясняет, при какой записи вычисления вып олнять легче (если устно вычислять трудно, используют пись менные приёмы вычислений, а когда это легко — устные).

Далее надо провести работу по учебнику, выполнив сложение чисел 45 и 23 так же, как сложение чисел 54 и 32: рассмотреть запись на предметном абаке; выяснить, какие числа надо слож ить и сколько в каждом из них десятков и единиц; объяснить по данной записи устный приём сложения чисел 45 и 23, а по том письменный приём сложения этих чисел. Учитель обращает внимание детей на предложения в объяснении, выделенные син им цветом, и поясняет, что эти предложения составляют план объяснения письменного приёма сложения или алгоритм. Полезно при этом зар анее подготовить Памятку и прикрепить её к доске:

1)      Пишу...

2)      Складываю единицы...

3)      Складываю десятки...

4)      Читаю ответ...

Эта Памятка помогает детям освоить алгоритм. Руководствуясь ею, дети решают примеры из упражнения № 1 (с. 4), устно комментируя решение.

Как правило, к каждому уроку наряду с упражнениями по закреплению вновь введённого материала в учебнике даны зад ания для закрепления и систематизации ранее изученного материала — это текстовые арифметические задачи, задачи геом етрического содержания, решение уравнений, составление и про верка равенств и неравенств и др.

В урок ознакомления с приёмом письменного сложения вклю чена текстовая задача № 2 в два действия. При решении первой из них можно предложить детям выполнить чертёж по услов ию задачи, затем провести работу по составлению плана реше ния: «Можем ли сразу узнать, сколько метров ситца портниха отрезала от куска? Почему не можем? (Не знаем, сколько метр ов ситца она отрезала на передник.) А это можно узнать? (Да.)» Дети намечают план решения и решают задачу.

Упражнение на сложение и вычитание (устные приёмы вычислений) дети могут выполнить самостоятельно дома (№ 3). Письменный приём вычитания для случаев вида 57 – 26 (с. 5) сходен с уже раскрытым приёмом сложения двузначных чис ел, поэтому можно использовать тот же методический приём: от устного приёма вычислений перейти к письменному.

Подготовкой к введению нового материала будет повторение десятичного состава двузначных чисел, а также устных приёмов вычитания вида 59 – 30, 79 – 6, 60 – 34. При рассмотрении приё ма для случая 60 – 34 следует обратить внимание, что вычита ние осуществляется по частям.

При введении нового приёма учитель предлагает детям реш ить пример 48 – 12. Ученики называют, сколько десятков и единиц в уменьшаемом, затем учитель иллюстрирует на предметн ом абаке число 48 в виде 4 пучков — десятков палочек и 8 отдельных палочек. Учитель говорит: «Будем вычитать по ча стям. Сколько надо убрать десятков? единиц?» (1 десяток и 2 единицы.) Запись имеет вид (48 – 10) – 2. Дети по записи вычисляют: 48 – 10 = 38, 38 – 2 = 36.

Возвращаясь к иллюстрации, учитель спрашивает: «Сколько десятков было сначала? Сколько убрали? Сколько было единиц сначала? Сколько убрали?» Делается вывод: десятки вычитали из десятков, а единицы — из единиц.

Решение примера 57 – 26 рассматривается по учебнику (с. 5). Сначала, используя иллюстрацию в учебнике, ученики объя сняют устный приём вычитания: (57 – 20) – 6 = 31. «Число 26 вычитаем по частям: сначала из 57 вычитаем 20

(или 2 дес.), получится 37; затем из 37 вычитаем 6, ответ: 31.»

Учитель объясняет, что при вычитании, как и при сложении, удобнее записывать числа одно под другим. Чтобы легче было выполнять вычисления (образец дан на с. 5 учебника), десятки записывают под десятками, единицы  — под единицами. Вычитан ие начинают с единиц. Ученики читают объяснение письменног о вычитания по учебнику, после чего учитель прикрепляет на доске Памятку, на которой в порядке следования записаны основные операции (алгоритм):

1.    Пишу…

2.    Вычитаю единицы...

3.    Вычитаю десятки...

4.    Читаю ответ...

Для закрепления знания алгоритма вычитания детям предлагают решить, пользуясь Памяткой, примеры № 1 (1, 2, 3-й столбики), устно комментируя их решение. Оставшие ся 4-й и 5-й столбики из № 1 и примеры из № 4 можно предл ожить для самостоятельной работы в классе и дома. Для закрепления ранее изученного материала выполняют решение текстовой арифметической задачи № 2. Содержание задачи № 2 полезно проиллюстрировать, изобразив шары разн оцветными кружками, или выполнить чертёж. После составлен ия плана решения ученики решают задачу самостоятельно.

Упражнение № 3 предназначено для закрепления знаний о ломаной. Учитель предлагает детям рассказать всё, что им изв естно об этой геометрической фигуре; сосчитать, сколько зве ньев составляет данную ломаную; рассказать, как узнать её длину разными способами. Чтобы начертить такую ломаную, как на чертеже, надо сначала поставить точки, являющиеся концами звеньев, затем соединить их отрезками. Дети объясняют, как правильно отсчи тывать клеточки тетради, чтобы поставить точки так же, как в учебнике (например, первую точку ставим в вершине угла квад рата — клеточки, вторую — отсчитав от первой точки 6 клето чек вправо, затем 2 клеточки вверх; третья точка расположена вправо от второй на расстоянии 6 клеточек, а четвёртая — на 2 клеточки вниз от третьей и на 14 клеточек вправо). После этог о ученики измеряют длину каждого звена ломаной и находят сумм у полученных чисел: 3 см + 3 см + 7 см = 13 см.

Следующие два урока (с. 6—7) отводят закреплению умений выполнять письменное сложение и вычитание двузначных чисел в отношении рассмотренных случаев и вместе с тем вводят проверку письменного сложения и вычитания для этих случа ев. Здесь также выполняется закрепление ранее изученного ма териала.

1.       Для закрепления изученных приёмов письменного сложе ния и вычитания предлагают решить примеры 15 + 83 и 76 – 42 с подробным объяснением, используя Памятку, после чего дети решают самостоятельно примеры 57 – 27 и 64 + 23.

2.       Чтобы ввести проверку письменного сложения, сначала на до предложить детям выполнить упражнение № 6. Вызванн ые ученики объясняют, как заполняли таблицу: если изв естны слагаемые, то находим сумму сложением; если же известны сумма и одно из слагаемых, то другое слагаемое находим вычитанием — из суммы вычитаем данное слагаем ое.

Ознакомить с проверкой письменного сложения можно, выпол няя упражнение № 1 (с. 6): ученики рассматривают иллюстрац ию к примеру 35 + 24 и решают его с устным комментирова нием. Затем решают второй пример (59 – 24). Учитель предла гает сравнить эти примеры и объяснить, как получен второй при мер из первого. Ученики отвечают: «Во втором примере из сум мы 59 вычли второе слагаемое 24 и получили первое слагаемое 35, значит, сложение выполнено правильно». Так же сравнива ют третий пример (59 – 35) с первым, после чего дети объяс няют, что при проверке сложения можно из суммы вычесть втор ое слагаемое, и если получится первое слагаемое, то пример на сложение решён правильно, а если не получится, значит, в вычислениях допущена ошибка (ч. 1, с. 84).

На следующем уроке наряду с решением примеров на слож ение и вычитание двузначных чисел (с. 7) надо рассмотреть проверку письменного вычитания с помощью сложения. Здесь можно использовать тот же методический приём, что и при рас смотрении проверки письменного сложения. Сначала дети выпол няют упражнение № 5, в результате чего устанавливают связь между числами при вычитании: если сложить вычитаемое и разность, то получится уменьшаемое. После этого учитель предлаг ает решить пару примеров: один — на вычитание двузначных чисел, а другой — на сложение вычитаемого с разностью, на пример: 86 – 32 и 32 + 54. В результате сравнения этих пример ов дети делают вывод, как проверить решение примеров на вы читание сложением: надо сложить вычитаемое с разностью; есл и получится уменьшаемое, то пример на вычитание решён пра вильно, а если не получится — в вычислениях сделана ошибка (ч. 1, с. 86). В учебник включены задания для закрепления умения выполнять письменное сложение и вычитание с проверкой (с. 6, № 2; с. 9, № 2; с. 10, № 6 и др.).

Задания, представленные на с. 6—7, дают возможность зак репить и обобщить ранее изученный материал.

1. Упражнения для закрепления знания приёмов устных вы числений и навыков в отношении табличных случаев сложения и вычитания (с. 6, № 5, 6; с. 7, № 4, 5, 7) выполняют не толь ко функцию закрепления умения вычислять и овладевать вычис лительными навыками, но и другие. Так, при выполнении упражн ения № 5 (с. 6) ученики закрепляют умение находить значения буквенных выражений при заданных значениях букв, знание терминов, относящихся к выполнению арифметических действий (сумма, слагаемые, разность, уменьшаемое, вычитаемое, значе ние суммы, значение разности). Важно, чтобы при выполнении этих упражнений и других, им подобных, дети сами пользовались соответствующими терминами. Для этого учителю надо чаще акцентировать на этом внимание («Прочитайте пример, исполь зуя названия чисел при сложении, и решите его; прочитайте выражения и найдите его значение»). Особое вни мание надо уделить табличным случаям сложения и вычитания: дети должны знать таблицы сложения и вычитания наизусть, т. е. сразу называть сумму любых однозначных чисел (7 + 9 = 16) или разность двузначного и однозначного чисел, когда в резуль тате получается однозначное число (11 – 7 = 4). С этой целью на каждом уроке учитель предлагает для устного выполнения упраж нения в различных формах:

— Сумма каких однозначных чисел равна 9? 10? 11? ... 18?

— Какое число надо вычесть из 11 (12, 13, ..., 18), что- бы получилось 9 (8, 7, ..., 2)?

— Продолжите столбики примеров и решите их.

2 + 9 12 – 3          Как изменяется первое слага3 + 9 12 – 4            емое в первом столбике? Как из  ...          ...        меняется сумма?

9 + 9                  12 – 9

Так же надо сравнивать примеры во втором столбике. С этой же целью полезно использовать и игровые формы заданий: так называемые цепочки примеров, занимательные рамки, магическ ие квадраты, лабиринты, ребусы и др. (естественно, на разных уроках), представленные на полях учебника и в разделах «Что узнали, чему научились». Дети устно называют ответ или показывают его на карточках с цифрами.

2. Продолжается работа по формированию умений решать простые и составные арифметические задачи. При решении простых задач на нахождение неизвестных компонентов (с. 6, № 3, 4) целесообразно воспользоваться схематическим чертеж ом, который выполняется под руководством учителя.

— Прочитайте задачу № 3. Что известно? Что требует-ся узнать? Выполним чертёж к задаче. Сколько деревьев решили посадить? (30.) Начертите отрезок, например, длиной 9 см. (Учи тель выполняет чертёж на доске.) Запишем под отрезком чис ло 30. Что ещё известно в задаче? (Осталось посадить 8 дерев ьев, когда несколько уже посадили.) Как это показать на чертеже? (Вызванный ученик подчёркивает часть отрезка и делает запись: 8.) Что надо узнать в задаче? (Сколько деревьев посад или осенью.) Покажите это на чертеже. (Вызванный ученик выд еляет оставшуюся часть отрезка и записывает «?».) Получается чертёж:

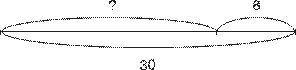
— Как узнать, сколько деревьев посадили осенью? (Надо вычесть 8 из 30, получится 22. Ответ: 22 дерева.) Объясните, почему надо вычитать. (Из 30 деревьев 8 осталось посадить, зна чит, их не посадили, а осенью посадили остальные.)

Ученик обр ащается к чертежу. Задачу № 4 (с. 6) можно предложить для самостоятельного решения.

Для проверки решения таких задач полезно предлагать детям составлять обратную задачу и решать её, после чего устанавливать, соответствует ли ответ обратной задачи условию данной. Напри мер, ученики составили к задаче № 4 (с. 6) такую обратную зад ачу: «В парке посадили 75 саженцев деревьев. Из них прижил ось 65 саженцев, а остальные вымерзли. Сколько саженцев дер евьев вымерзло?» Дети решают эту задачу: 75 – 65 = 10. От вет: 10 деревьев. Сравнив ответ обратной задачи с числовыми данными проверяемой задачи, дети говорят, что данная задача решена правильно, так как согласно условию вымерзло 10 саженц ев, и при решении обратной задачи тоже получили 10 сажен цев.

При решении составных арифметических задач (с. 7,

№ 1) можно, пользуясь Памяткой, провести их разбор под руковод ством учителя, после чего предложить детям самостоятельно за писать решения.

Задачу № 3 (с. 7) можно использовать для развития у дет ей представления о времени движения. С этой целью полезно предложить им такие вопросы: «Почему полёт на самолёте занял меньше времени по сравнению с поездкой на поезде? Сколь ко времени сэкономил пассажир, полетев на самолёте?»

Упражнение геометрического содержания, данное на полях с. 6, следует выполнить под руководством учителя.

Для ознакомления с видами углов предназначен материал учебника на с. 8—9.

Сначала надо повторить сведения, известные детям прямой, отрезке и луче. Учитель на доске, а дети на отдельных листах бумаги чертят эти фигуры и сравнивают их, находя сходство (их чертят по линейке) и различия (отрезок ограничен с двух сторон — имеет и начало, и конец; прямая не ограничена — не имеет ни начала, ни конца; луч ограничен с одной стороны — имеет начало, но не имеет конца).

Затем дети под руководством учителя строят угол — проводят два луча из одной точки, показывают стороны и вершину угла. На подвижной модели угла (две полоски картона, соединённые кнопкой) учитель демонстрирует, как изменяется угол в зависим ости от положения одной его стороны относительно другой. Дет и убеждаются, что углы бывают разными. Ставится учебная за дача: научиться распознавать виды углов и запомнить их назва ния.

Далее в учебнике показано, как ввести понятие прямого угл а. Дети получают его модель двойным перегибанием листа бум аги непрямоугольной формы, а затем с помощью наложения убеждаются, что у всех получились одинаковые углы (так как совпали сторон ы и вершины углов).

С помощью бумажной модели учащиеся находят прямой угол на чертёжном угольнике и в дальнейшем используют его в ка честве модели прямого угла.

Для закрепления знаний о видах углов дети читают текст в учебнике и с помощью модели прямого угла определяют виды уг лов, которые даны на поле (с. 8).

Прежде чем определять виды углов многоугольников, следует рассмотреть начерченный на доске, например, пятиугольник с двум я прямыми углами. Учитель поясняет, что в этом случае углы образованы соседними сторонами данной фигуры, а вершины — пересечением сторон^[4]. Вызванные к доске ученики показывают стороны и вершины каждого угла и с помощью модели прямого угла определяют его вид.

На следующем уроке продолжается работа по закреплению представлений о видах углов. Детям предлагают самостоятельно начертить фигуры, имеющие прямые углы (с. 10, № 4). Можно выполнить задание по вариантам: I вариант — № 4 (1), II ва риант — № 4 (2). Учитель вызывает по одному ученику — пред ставителю от каждого варианта — для работы на доске, они выполняют её, объясняя своё решение вслух. Остальные дети оценивают их работу и предлагают своё решение, если оно отличается от предложенного. Выясняется, что вычерчивание фигур, имеющих прямой угол, надо начинать с прямого угла. На этих уроках (с. 8—10) проводится работа по закреплению ран ее изученного материала.

1.       Выполнение упражнений № 2, 3 (с. 9) и упражнений № 5, 6 (с. 10) позволяет повторить ранее изученные вы числительные приёмы и закрепить вычислительные умения и навыки. Большинство из этих упражнений можно предлагать для самостоятельного выполнения в классе или дома. До или после выполнения перечисленных упражнен ий полезно предлагать задания на развитие познавательных УУД. Например, до решения примеров из № 2 (с. 9) спрашивают: «Чем похожи эти примеры? Сравните примеры на сложение и скажите, не вычисляя: в каком из них будет самая больш ая сумма?» До решения примеров из № 3 (с. 9) можно задать вопросы: «Чем похожи и чем различаются приме ры первого и второго столбиков? В каком примере третье го столбика надо изменить вычитаемое, чтобы все примеры этого столбика были похожими?»

2.       Продолжается работа по формированию умений решать текстовые арифметические задачи: это задача № 4 на с. 9, заданная выражением, и задачи № 1, 2, 3 (с. 10). Рассмотрим, как можно провести работу по составле нию задачи на с. 9. Желательно вначале рассмотреть простейшие выражения (например, 9 + 6, 15 – 8) и вспом нить, какие задачи можно составить по ним. Затем прис тупают к составлению задачи по выражению (например, (12 + 7) – 3). Опираясь на выводы, которые дети сделают в подготовительной работе, выбирают вопрос задачи. Наприм ер, будем узнавать, сколько осталось после того, как изр асходовали (продали, отдали) 3 кг (3 м, 3 л и т. п.). Далее выясняют, как в условии задачи будет представлено то, что расходуют (продают, отдают). Это могут быть две части чего-то целого (2 ящика с фруктами, 2 куска мате рии, 2 бидона молока и т. п.).

Можно начать анализ выражения с первого действия и использовать другие виды простых задач — увеличение и уменьш ение числа на несколько единиц. При этом можно сразу дого вориться о предметной области задачи (про что будет задача) — про 3 куска материи, или про 3 мешка картофеля, или про по купку тетрадей тремя учениками и т. п. Разумеется, следует по буждать детей составлять раз ные по сюжету задачи, с тем чтоб ы, сравнив их, учащиеся убеждались в их математическом сходс тве — они все решаются одинаково.

Задача, приведённая на полях с. 9, в которой требуется найт и недостающие фигуры для постройки грузовика, и другие подобные задания имеют целью развитие у детей способности конструирования новых фигур из данных, умения выделять из данн ой фигуры составляющие её другие фигуры. Сначала, рассмотр ев рисунок грузовика, дети называют, из каких фигур он составлен. Затем называют фигуры, изображённые под грузовик ом, и находят их место в рисунке грузовика или же выполняю т свой рисунок грузовика, используя эти его части. Теперь легк о назвать фигуры, которых не хватает: одного колеса, полови ны кузова (большой треугольник) и части кабины (маленький тре угольник).

Заметим, что подобные задания дети выполняют с большим интересом, при этом, как правило, сами находят несколько спо собов решения.

На полях с. 10 дана головоломка. Так как её решение может вызвать затруднения у части детей, его следует выполнять под руководством учителя. После того как дети разложат 9 счётных палочек одинаковой длины (см. рис.), учитель говорит, что один треугольник уже образовался из разложенных палочек, и просит показать сначала его, а затем остальные палочки.

— Эти палочки лежат парами. Покажите одну из пар.  Как получить треугольник, в который входили бы обе палочки этой пары? (Положить палочку из другой пары, которая соединит конц ы палочек первой пары.) Сделайте это. Сколько получилось тре угольников? (2.) Сколько треугольников должно получиться? (3.) Как получить третий треугольник? (Соединить концы третьей па ры палочек, используя оставшуюся палочку от второй пары.) Вы полните. Полезно рассмотреть другие варианты решения.

Для проверки усвоения изученного материала надо чаще проводить ма тематические диктанты, включающие задания на вычисления, текстовые арифметические задачи, развивающие занимательные упражнения.

Выполнение задания № 8 (с. 11) формирует умение читать несложные готовые таблицы, понимать их смысл, извлекать информацию, заложенную в каждой ячейке, строке, столбце таблицы. Задание выполняется устно: дети читают задание, рассматривают таблицу, рассказывают, что отражено в её строках, столбцах, ячейках, отвечают на предложенные вопросы.

В качестве подготовки к рассмотрен ию новых случаев письменных приёмов сложения для случаев вида 37 + 48 и 37 + 53 (с. 12, 13) следует повторить табличные случаи сложения с переходом через десяток и десят ичный состав чисел второго десятка, предложив детям решить примеры вида 7 + 8, 8 + 9 и т. п., сопровождая решение кажд ого примера вопросом:

«Сколько десятков и сколько единиц в полученном числе?»

Следует решить на доске с подробным объяснением один-два примера вида 42 + 36 с использованием Памятки, на которой записан алгоритм сложения.

При ознакомлении с новым случаем письменного сложения двузначных чисел можно предложить детям решить с объяснени ем пример 38 + 56. Один ученик записывает решение на доске, а остальные — в тетрадях, объясняя решение:

38 + 56 = 38 + (50 + 6) = 88 + 6 = 94.

Учитель предлагает записать решение этого примера в столб ик и объяснить его. Вызванный ученик записывает решение на доске и объясняет: «Пишу десятки под десятками, а единицы под единицами; складываю единицы: к 8 прибавить 6, получится 14». Учитель говорит: «В числе 14 есть не только единицы, но и де сяток, его надо запомнить и прибавить к десяткам, а под единиц ами записать число единиц — 4. Сложите десятки. (3 + 5 = 8.) Но ещё получился 1 десяток из единиц. Сколько всего получит ся десятков? (8 + 1 = 9.) Назовите ответ. (94.)»

Для закрепления дети читают по учебнику объяснение реше ния примера 37 + 48 (с. 12 вверху), затем выполняют упражне ние № 1 (с. 10) (один-два примера под руководством учителя, остальные — самостоятельно).

Аналогично строится работа над алгоритмом сложения для случ аев вида 37 + 53. Особенность приёма сложения для этих слу чаев состоит в том, что, сложив единицы данных двузначных чис ел, получим 10 (или 1 дес.), а единиц будет 0. В качестве под готовки к пониманию детьми этой особенности в учебнике пред усмотрены специальные упражнения (с. 12, № 5 (3-й столбик); с. 13, № 6 (3-й столбик). Например, отвечая на вопрос: «Сколь ко десятков и сколько единиц в числе 40?», дети должны ответить: 4 дес. и 0 ед.

Для закрепления ранее пройденного материала в учебник е (с. 12, 13) предусмотрены специальные упражнения:

1.       Выполняя упражнения № 2, 5, 6 (с. 12) и № 2, 6 (с. 13), дети закрепляют знание вычислительных алгоритмов и вычислительные умения и навыки. На каждом уроке учителю надо дополнительно предлагать для устной работы составленные им упражнения, уделяя при этом осо бое внимание табличным случаям сложения и вычитания в пределах 20. Например: «Сумма каких однозначных чис ел равна 11? 12? Какое число надо вычесть из 14, чтобы получить 9? 6?» И т. п.

При выполнении упражнения № 5 (1-й и 2-й столбики) (с. 12) и упражнения № 5 (1-й и 2-й столбики) (с. 13) учитель напоминает, что в этих случаях прибавляют и вычитают числа по частям. Например, при решении примера 37 + 8 дети рассуждают так: «8 — это 3 и 5, прибавлю к 37 сначала 3, получится 40, затем к полученному числу приб авлю 5, получится 45», а выполняя вычитание 60 – 32, объясняют: «32 — это 30 и 2, вычту из 60 число 30, по лучу 30, затем вычту из 30 число 2, получится 28». В дальнейшем ученики сразу называют ответ, выполняя отдельные операции про себя.

2.       На рассматриваемых уроках предлагаются для решения задачи составные (с. 12, № 3; с. 13, № 4) и простые (с. 12, № 4; с. 13, № 3). Составные задачи можно предлагать для самостоятельного решения с опорой на задания Памятки, после чего дети объясняют своё решение. При этом полезно предлагать ученикам вопросы, ответы на которые позволят им установить новые связи между величинами, данными в задаче. Так, после решения задачи № 3 (с. 12) спрашивают: «Можно ли решить эту задачу друг им способом? Как можно изменить данные задачи, чтобы её можно было решить разными способами?» После ре шения задачи № 4 (с. 13) детям предлагают изменить вопрос задачи так, чтобы она решалась одним действием. После устного решения каждой из простых задач полезно дать задание: «Составьте и решите задачи, обратные дан ной».

3.       Решение уравнений (с. 13, № 5) дети выполняют спосо бом подбора неизвестного числа с последующей провер кой решения. В тех случаях, когда подобрать искомое чис ло трудно, предлагается проверить два-три данных учителем числа.

4.       Упражнения на смекалку, данные на полях с. 12 и 13,учит ель предлагает для самостоятельного выполнения. Если большинство детей затрудняются выполнить решение, учит ель ставит вопросы, направляющие мысль детей на пра вильное решение, но не подсказывает его. Так, решая задачу «Какая фигура лишняя?» (с. 12), достаточно спросить детей: «Из чего составлена каждая фигура и сколько клеточек в каждой из них?» Теперь легко установить лишнюю фигуру — она состоит из 5 клеточек, тогд а как в остальных по 4 клеточки. (Можно установить лишнюю фигуру и по другому признаку — цвету.)

Упражнение на полях с. 13 «Продолжи ряд» труднее. Учи тель говорит: «Чтобы продолжить ряд, надо установить законом ерность, по которой получено каждое следующее число в данн ом ряду. Назовите данные числа. (1, 3, 7, 13, 21.) Сколько ещё чисел надо записать в этом ряду? (3.) Как изменяются числа в этом ряду? (Увеличиваются.) Давайте узнаем, на сколько единиц увеличено каждое следующее число по сравнению с предыдущим. На сколько единиц увеличено второе число по сравнению с перв ым? (На 2.) третье число по сравнению со вторым? (На 4.) Назовите, на сколько единиц увеличено четвёртое число по срав нению с третьим и пятое число по сравнению с четвёртым. (Чет вёртое на 6, пятое на 8.) Запишите в ряд числа, которые показ ывают, на сколько увеличивали каждое следующее число. (На 2, 4, 6, 8.) Кто догадался, какое следующее число будет в этом ряду? (10.) Что оно показывает? (Число, которое следует за числ ом 21, будет на 10 больше; это число 31.) Назовите два чис ла, которые следуют за числом 31. (43 и 57.) Как получили 43? (31 + 12.) 57? (43 + 14.)»

При ознакомлении с прямоугольником учитель может использ овать материал учебника, данный на с. 14, 15. Здесь же предусмотрен материал для закрепления представлений о прямоугольнике.

Для ознакомления с прямоугольником надо использовать наглядные пособия: вырезать из плотной бумаги и прикреп ить на доску 2—3 прямоугольника, четырёхугольник с одн им прямым углом, с двумя прямыми углами и четырёх угольник, в котором нет прямых углов. Детям предлагает ся найти в этих фигурах прямые углы с помощью чертёж ного угольника. В результате этой работы они увидят, что в четырёхугольниках может быть один прямой угол, два прямых угла или все четыре угла могут быть прям ыми. Ученики вспоминают, что четырёхугольник, у которого все углы прямые, называется прямоу гольником.

Аналогичная работа проводится по рисункам учебника (с. 14). Ученики читают определение прямоугольника. Для закрепления полученных знаний надо выполнить упражнение № 1 (с. 15). Учен ики находят прямоугольники, установив предварительно с помо щью чертёжного угольника, что все углы у этих четырёхуголь ников прямые. Задание № 2 (1 и 2), данное на с. 14, дети вып олняют под руководством учителя:

— Сегодня вы будете учиться чертить фигуры с пря- мым углом. Прочитайте упражнение № 2 на с. 14. Начертим сначала треугольник с прямым углом. Что надо начертить сначала? (Пря мой угол.) Воспользуемся чертёжным угольником. Покажите на чертёжном угольнике прямой угол, его вершину и сторон ы. Расположите чертёжный угольник в тетради так, чтобы вершина его прямого угла совпадала с вершиной угла одной из клеточек. Теперь по чертёжному угольнику проведите сторо ны прямого угла: чтобы получился треугольник с прямым углом, надо отметить на каждой из сторон прямого угла по одной точк е и соединить их отрезком.

На следующих уроках дети выполняют остальные задания из упражнения № 2, т. е. чертят четырёхугольник, у которого два угла прямые, а другие непрямые. Причём чертежи выпол няют на клетчатой бумаге, пользуясь чертёжным треугольником.

Здесь, как и на предыдущих уроках, дан материал для зак репления ранее изученного:

1.       Упражнения на вычисления (с. 14, № 6; с. 15, № 5, 7) ученики выполняют преимущественно самостоятельно. По указа нию учителя дети устно объясняют решение.

Для устных вычислений предназначена игра «Набери 15». Ис пользуя числа в окнах избушки, дети записывают суммы чисел, значения которых равны 15. Например: 7 + 8 = 15, 6 + 9 = 15, 7 + 3 + 5 = 15 и т. д.; эту избушку можно использовать и на дру гих уроках, заменяя число 15 другими числами. Победителем в этой игре считается тот ученик, который составил правильных сумм больше других.

Этим же целям служит упражнение на заполнение пустых клеток магических квадратов, которые даны на полях с. 15. Дети объясняют, почему эти квадраты называли магическими. Выясняется, как найти числа в пустых клетках этого квадрата: сначала надо вычислить сумму чисел, которые стоят в одном ряду. В первом магическом квадрате это сумма чисел 10 + 8 + 6 = 24. Значит, сумма чисел в нижнем ряду также буд ет равна 24. Известно, что в нижнем ряду есть числа 11 и 6; чтобы найти третье число, достаточно из 24 (из суммы трёх чи сел) вычесть сумму данных чисел в этом ряду (11 + 6 = 17); выч итаем: 24 – 17 = 7. Рассуждая аналогично, легко найти числа, стоящие в остальных клетках.

2.       При выполнении упражнения № 5 (с. 14) на сравнение выражений надо спросить детей: «Какой знак вы поставите, не вычисляя значений выражений? Почему?» После этого выполня ют проверку, вычислив значения выражений.

3.       Выполняя упражнение № 8 (с. 15) на нахождение зна чений буквенных выражений, дети сначала называют числовые значения букв и устанавливают, как изменяются эти значения: убывают или возрастают; после этого находят значения выражен ий, сравнивают их и делают вывод, как изменялась разность, если уменьшаемое возрастало, а вычитаемое не изменялось, и как изменялась сумма, если одно слагаемое возрастало, а другое не изменялось.

На каждом из рассматриваемых уроков предлагаются для решения текстовые арифметические задачи, причём к большинс тву из них даются дополнительные задания творческого характ ера. Так, в задаче № 3 (с. 14) требуется подобрать одно из дан ных и решить её, используя это данное. Учитель спрашивает: «Сколько рублей могла истратить бабушка, если у неё было 50 рублей? (Назовите самое большое число, самое маленькое число.) Сколько рублей осталось у бабушки? Назовите решение (50 – 50 = 0, 50 – 0 = 50, в первом случае осталось 0 рублей, во втором все рубли, которые у неё были, — 50 рублей)». Учитель спрашивает, кто подобрал другие числа; вызванные ученики на зывают другие числа и решение в этом случае.

В задаче № 4 (с. 14) детям предлагается придумать вопрос к данному условию и решить задачу с этим вопросом. Это задан ие можно дать на выбор: дети ставят вопрос так, чтобы зада ча решалась двумя действиями либо одним, после чего каждый решает свою задачу.

Задачи № 2 и 3 (с. 15) можно предложить для самостоятель ного решения, а для проверки составить и решить обратные задачи. Задача № 4 (с. 15) — подготовительная к введению умножения. При её разборе можно предложить детям сделать рисунок и объяснить, что значит 3 таких ведра. По сколько литров воды Коля приносил в каждом ведре? (По 8 литров.) Как решить эту задачу? (8 + 8 + 8 = = 24. Ответ: 24 литра.) Какие слага емые в этой сумме? (Одинаковые.) Сколько одинаковых слагае мых? (3.)

На ознакомление с письменным приёмом сложения для слу чая вида 87 + 13, приёмом, закрепляющим умение выполнять соответствующие случаи сложения, а также закрепляющим ранее изученный материал, отводятся следующие два урока (с. 16, 17).

Алгоритм для этого случая включает новую операцию — здесь сумма десятков слагаемых равна 10, а 10 десятков — это одна сотня. Таким образом, в сумме получается трёхзначное число 100. Для понимания этой новой операции надо предложить детям вы полнить устно подготовительные упражнения вида 4 дес. + 6 дес., 2 дес. + 8 дес. и т. п. Сравнив примеры, ученики объясняют, что в ответах этих примеров получается 10 десятков, а это одна сот ня, или 100. Устно дети выполняют упражнение № 2 (с. 16), предварительно объяснив, что значит дополнить число до 100. При ознакомлении с этим новым приёмом ученики решают примеры, руководствуясь известным им алгоритмом. Допустим, пред лагается решить пример 14 + 86. Ученик объясняет: «Пишу един ицы под единицами, а десятки под десятками. Складываю един ицы: 4 + 6 = 10, 10 ед. — это 1 дес. и 0 ед., пишу под единицами 0, а 1 дес. запомню и прибавлю к десяткам. Складываю десятки: 1 дес. + 8 дес. = 9 дес. и ещё 1 дес., который пол учился от сложения единиц, всего будет 10 дес., а это 1 сотня и 0 дес.; пишу под десятками 0, а 1 сотню пишу на третьем мес те, считая справа налево; значит, 14 + 86 равно 100. Для закрепления знания рассмотренного приёма ученики ре шают примеры № 1, 5 (с. 16), устно объясняя решение вслух или про себя.

Другие упражнения этих уроков предназначены для закреп ления ранее изученного материала и подготовки к изучению нового.

1.       Текстовые арифметические задачи (с. 16, № 3, 4, 6; с. 17, № 4, 5, 6) ученики могут решить самостоятельно, использ уя Памятку, некоторые задачи целесообразно решить устно, нап ример задачу № 3 (с. 16). К задаче № 5 (с. 17), решение кот орой служит подготовкой к умножению, требуется сделать схе матический рисунок. Рулоны можно изобразить прямоугольникам и и около каждого из них записать его длину. Например:

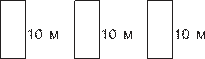
Теперь легко решить задачу, выполнив сложение: 10 + + 10 + 10 = 30. Ответ: 30 м. После этого дети сравнивают слагаемые и заключают, что они равны, они одинаковые, и считают, сколько в сумме одинаковых слагаемых. (3.) В тех же целях предлагаетс я решить устно примеры № 7 (с. 16). После решения учитель спрашивает: «Чем похожи все эти примеры?» (Здесь прибавлял и и вычитали одинаковые числа, таких чисел три.)

2.       Упражнение на восстановление пропущенных скобок (с. 17, № 2) может быть выполнено не только простым перебором реш ений, но и на основе анализа выражения и сравнения данных чисел со значением выражения. Например, 40 – 8 + 7 = 25. Учи тель спрашивает: «Какое число должно получиться в ответе? Сколько надо вычесть из 40, чтобы получилось 25? (15.) Как получить 15 из чисел, данных в выражении?» (Надо поставить скобки: 40 – (8 + 7) = = 25.) И т. п.

3.       Решая ребусы, данные на полях с. 16, ученики объясняю т, какие действия требуется выполнить в примерах, что надо сделать, чтобы записать примеры, как выполнить проверку. Учит ель спрашивает: «Как найти число единиц в первом слагаемом?» Ученик рассуждает: «Я подумаю, к какому числу единиц надо прибавить 8 ед., чтобы получить 8 ед., — это нуль единиц, знач ит, первое слагаемое 20. Подумаю, какое число десятков надо прибавить к 2 дес., чтобы получить 7 дес., это 5 дес., второе слагаемое будет 58.

Пишу пример и проверяю:

   20 +

 58

   78

Цифры подобраны правильно». Аналогично решают второй ребус.

На следующих двух уроках (с. 18, 19) дети знакомятся с новыми письменными приёмами вычитания для случаев вида 40 – 8 и 50 – 24.

В качестве подготовки дети решают устно примеры 30 – 6, 60 – 5 и др., объясняя так: «30 – 6: 30 — это 20 и 10, вычту 6 из 10, получится 4 да ещё 20, всего 24». По учебнику дети объясн яют решение примера 40 – 8.

Учитель предлагает выполнить решение этого примера столб иком. Ученики объясняют: «В вычитаемом только единицы, пишем их под единицами; вычесть 8 ед. из 0 ед. нельзя, берём 1 дес. из 4 дес., остаётся 3 дес. (Чтобы не забыть, что взят 1 дес., ставим точку над цифрой 4.) 1 дес. — это 10 ед., вычи таем 8 из 10, получается 2. Пишем 2 под единицами и 3 на ме сте десятков. Всего 32». Для закрепления знания этого приёма дети решают примеры № 1 (с. 18).

На следующем уроке (с. 19) дети знакомятся с письменным приёмом для случаев вида 50 – 24. Как и в других случаях, снач ала дети решают этот пример устно, по записи в учебнике: 50 – 24 = (50 – 20) – 4 = 26. Затем учитель предлагает записать решение этого примера столбиком и объяснить решение так, как это сделано на с. 19. Для закрепления знания этого алгоритма учит ель предлагает решить примеры № 1 (с. 19).

На этих же страницах учебника (с. 18, 19) даны упражнен ия для закрепления ранее изученного материала.

1. Решение текстовых арифметических задач разными способ ами (с. 18, № 3; с. 19 — задания для самопроверки). После чтения и краткой записи каждой задачи дети рассказывают, как они представляют себе то, о чём говорится в задаче.

— Скажите, как могла расплачиваться Катя за покуп- ку. (Могл а дать в кассу 10 р., а могла 50 р. или же все свои деньги.)

— Как будете решать задачу, если Катя подала в кас- су 10 р.? (Сначала узнаю, сколько сдачи она получит: 10 – 8 = 2; теперь узнаю, сколько всего денег осталось у Кати: 2 + 50 = 52. Ответ: 52 р.)

— Как будете решать задачу, если Катя подала в  кассу 50 р.? (Дети решают аналогично первому способу:

50 – 8 = 42, 42 + 10 = 52. Ответ: 52 р.)

— Как ещё можно решить эту задачу? (Сначала узна- ем, скольк о всего денег было у Кати: 10 + 50 = 60. Потом сколько денег осталось у Кати: 60 – 8 = 52. Ответ: 52 р.) Учитель предлагает сравнить эти решения (решали поразном у, а ответы везде одинаковы, значит, задача решена правильн о). Полезно выяснить, при каких изменениях условия задачу нельзя было бы решить разными способами.

На следующем уроке можно предложить самостоятельно реш ить разными способами задачу для самопроверки (с. 19), выполнив предва рительно схематический чертёж.

Задачи № 2 (с. 18) и № 2 (с. 19) можно записать кратко, и дети решают их самостоятельно.

2.       Уравнения № 6 (с. 18) и № 3 (с. 19) можно предложить для устного решения способом подбора с проверкой.

3.       При решении ребусов, данных на полях с. 18, сначала уча щимся предлагают попытаться самим записать зашифрованные в ребусах примеры, например при работе в парах, после чего для проверки вызванные ученики объясняют, как они получили эти примеры, а другие проверяют по своим записям.

4.       Упражнение на полях с. 19, в котором требуется найти лишнее выражение, учащиеся легко выполняют самостоятельно, после того как вычислят значения данных выражений и сравнят их. Учитель может дополнительно предложить такие задания: «Придумайте свои выражения (лишнее и нелишнее) в данном ряду; скажите, как надо изменить лишнее выражение, чтобы оно перестало быть лишним.

Далее на с. 22—27 представлена рубрика «Что узнали. Чему научились», в которой даны упражнения по материалу, уже изу ченному во 2 классе. Эти упражнения учитель может использов ать на уроках по закреплению ранее пройденного материала, а также для самостоятельных и контрольных работ.

На следующих уроках (с. 29—31) предусматривается изуч ение нового письменного приёма вычитания для случаев вида 52 – 24, проведение подготовительной работы к введению действия умножения, а также работы по закреплению ранее изу ченного материала.

Подготовкой к ознакомлению с письменным приёмом вычитан ия является воспроизведение устного приёма. Используя рисун ок и записи на с. 29, дети решают пример 52 – 24, вычитая числ о 24 по частям: сначала 20, потом из полученного числа (из 32) вычитают 4, получается 28. Учитель предлагает изучить по учебнику, как решить этот пример, записывая вычислен ия столбиком, и продолжить объяснение: «Вычитаю десятки: бы ло 5 дес., но 1 дес. взяли при вычитании единиц; осталось 4 дес.; 4 дес. – 2 дес. = 2 дес., пишу под десятками 2. Читаю от вет: разность равна 28».

Для закрепления знания нового приёма вычитания ученики решают примеры № 1 (с. 29), № 1 (с. 30), № 1 (с. 31), запис ывая их решение столбиком, устно объясняют решение некоторых примеров.

На этих же уроках в плане подготовки к ознакомлению с дей ствием умножения предлагаются упражнения на нахождение сумм ы одинаковых слагаемых и на вычитание из данного числа оди наковых чисел.

Так, после решения каждого примера на сложение из упраж нения № 5 (с. 29) учитель спрашивает: «Какие числа прибавлял и к числу 32? к числу 18? (Одинаковые.) Сколько одинаковых чисел прибавили к 32? (3.) к 18? (2.) Какие числа вычитали из 27? из 14? (Одинаковые.) Какое число получалось в ответе? (Нуль.) Значит, в числе 27 содержится 3 раза по 9. Сколько раз содержится в числе

14 по 7?» (2 раза.)

Выполняя упражнения № 4, 5, 6 (с. 30), дети переходят от конкретной ситуации, описанной в задаче, к действию сложения одинаковых чисел.

Решая задачу № 4, дети рассуждают: «Пара носков — это 2 носка, таких пар 4, значит, чтобы узнать, сколько всего нос ков, надо выполнить действие сложения; число 2 взять слагаемым 4 раза: 2 + 2 + 2 + 2 = 8. Ответ: 8 носков». Чтобы ответить на вопрос задачи № 5, надо число 2 взять слагаемым 5 раз: 2 + 2 + 2 + 2 + 2 = 10. Ответ: 10 кружков. Отвечая на вопрос задачи № 6, берём число 3 слагаемым 4 раза: 3 + 3 + 3 + 3 = 12. Ответ: 12 кружков.

Выполняя упражнения № 4 и 5 (с. 31), можно показать, что в сумме могут быть не только 3—4 одинаковых слагаемых, но и больше (например, 12 — это сумма шести двоек, 16 — это сумма восьми двоек). Полезно предложить детям составить сумму одинаковых слагаемых, где складываются двузначные числа.

Как и на других уроках, здесь даны упражнения для закрепл ения ранее изученного материала.

1. Текстовые арифметические задачи № 2, 3 (с. 29) и № 2, 3, (с. 30) можно предложить для самостоятельного решения с помощью Памятки, а разбор провести только с теми детьми, которые затрудняются при решении.

Работу по решению задачи № 2 (с. 31) можно провести так: дети читают задачу, учитель говорит: «Подумайте, как можно по-разному (разными способами) решить эту задачу, и запишите решение одним из этих способов». Затем вызванный ученик зап исывает своё решение на доске, объясняя, что он находил, вы полняя каждое действие. Те ученики, у которых другой способ решения, записывают и объясняют своё решение. Теперь надо сравнить ответы, полученные при разных способах решения. Учит ель напоминает: если получены одинаковые ответы, значит, зад ача решена правильно.

Задачу № 3 (с. 31) дети могут решить дома.

Выполнять задание № 6 (с. 31) следует под руководством учителя. Дети записывают разность и находят её значение: 60 – 15 = 45, затем называют уменьшаемое (60), вычитаемое (15) и устно отвечают на поставленные вопросы. После этого запис ывают сумму данных чисел и её значение (60 + 15 = 75) и узнаю т, на сколько разность меньше суммы этих чисел (75 – 45 = 30), на сколько разность меньше уменьшаемого (60 – 45 = 15) и на сколько разность больше вычитаемого (45 – 15 = 30).

Решая эту задачу, все вычисления дети выполняют устно.

2.  Для закрепления знания ранее изученных алгоритмов вычис лений и выработки вычислительных навыков предназначены упр ажнения № 4 (с. 29), № 1 (с. 30), № 1 (с. 31), а также за дание на полях с. 29, в котором требуется выполнить вычисле ния и разбить выражения на две группы. Это упражнение дети могут выполнить разными способами (например, в одной группе будут выражения, значения которых равны 30, а в другой — те, значения которых равны 40; или так: в одной группе — суммы, а в другой — разности). Поиски разных способов классификации — одно из самых эффективных заданий на формирование познавательных УУД.

3.  Упражнение на подбор знака «+» или «–».

Учитель предлагает рассмотреть упражнение № 7 (с. 30): «Что требуется выполнить в этом упражнении? (Поставить пропущенн ые знаки «+» или «–», чтобы получилось верное равенство.) Объясните, как будете подбирать знаки действий в первой строке первого столбика». (Сравню первое число 63 с числом 50, которое будет значением выражения: 63 > 50, проб ую знак «–»: 63 – 20 = 43. Сравню числа 43 и 50: 43 < 50, пробую знак «+»: 43 + 7 = = 50. Читаю верное равен ство: 63 – 20 + 7 = 50.)

Рассуждая аналогичным образом, дети под руководством учи теля составляют другие верные равенства, записанные в первом столбике, и самостоятельно — во втором.

С опорой на понятия верного и неверного равенств решают уравнения (с. 31, № 7). Подставив вместо x число 18, дети объ ясняют, верное или неверное равенство получилось: 27 – 18 = 9 (верное равенство), записывают уравнения с решением и про веркой в тетрадях, например так:

27 – x = 9                                      x + 2 = 20 x = 18                                                x = 18 27 – 18 = 9                                       18 + 2 = 20

Подставляя 18 в уравнение 70 – x = 6, получаем неверное равенство: 70 – 18 = 6 (так как 52 не равно 6), делаем вывод о том, что 18 не является решением этого уравнения, и его выпи сывать не будем.

4. При выполнении упражнения на нахождение значений буквенных выражений при заданных значениях букв (с. 30, № 8) учитель предлагает прочитать задание, назвать значения буквы k, сравнить их и сказать, как они изменяются (возраста ют или убывают). Затем дети объясняют, значения каких выраж ений надо вычислить (разности k – 6 и суммы k + 8) и как будет изменяться значение разности и суммы; после вычисления разности и суммы проверяют сформулированные выводы.

На с. 32, 33 рассматриваются свойства сторон прямоугольн ика и осуществляется подготовка к введению умножения.

1. При ознакомлении со свойством сторон прямоугольника можно использовать рисунок прямоугольника, противопо ложные стороны которого выделены цветом, например крас ным и синим.

Объяснение можно провести так: «Какая это фигура? Как вы узнали? Стороны, которые изображены красным цветом, лежат одна напротив другой (против другой), поэтому их называют про тивоположными. Стороны, которые изображены синим цветом, тоже лежат одна напротив (против) другой, они тоже называютс я противоположными. У прямоугольника две пары противопол ожных сторон».

Учитель предлагает сравнить с помощью линейки противопол ожные стороны прямоугольника. Вызванный ученик сравнивает и устанавливает, что они равны.

Аналогичная работа проводится по учебнику (с. 32). Полезн о, кроме того, провести практическую работу: раздать детям вы резанные из бумаги (разные) прямоугольники и предложить срав нить противоположные стороны наложением, сгибая листок.

Для закрепления знания свойства противоположных сторон прямоугольника надо предложить детям прочитать по учебнику задание к упражнению № 1 (с. 32), внимательно рассмотреть рисунки и ответить на вопрос: «Почему теперь (рис. 2) нельзя сказать, что рамка имеет форму прямоугольника?» Дети отвеч ают, что у второй рамки углы не прямые, значит, это не прямоу гольник. В заключение учитель спрашивает: «Если известно, что у четырёхугольника противоположные стороны равны, то можно ли сказать, что это прямоугольник?» Ученики должны ответить, что не всегда такой четырёхугольник является прямоуголь ником, надо ещё знать, будут ли у этого четырёхугольника углы прямыми.

2.       В каждый из приведённых уроков (с. 32—33) следует вклю чать упражнения на закрепление письменных алгоритмов сложения и вычитания (с. 32, № 4; с. 33, № 7), а кро ме того, примеры из раздела «Упражнения для закреплен ия»;

дети выполняют задания самостоятельно, учитель помогает тем из них, кто затрудняется сам выполнить решение.

3.       На этих же уроках продолжается подготовительная раб ота к ознакомлению с умножением: ученики выполняю т упражнения на нахождение суммы одинаковых слагае мых и на замену данных чисел суммой одинаковых слага емых (с. 31, № 4, 5; с. 33, № 5, 6). Можно предложить детям такие упражнения: «Замени суммой двух одинаков ых слагаемых число 20, суммой трёх одинаковых слагае мых число 30. Продолжи».

4.       Текстовые арифметические задачи включены в матери ал каждого урока (с. 32, № 2, 3; с. 33, № 3). Пользуясь Памяткой, дети могут решать эти задачи самостоятельно, часть с записью решения, часть устно.

Задачу № 2 (с. 32) учитель предлагает прочитать, сказать, что известно и что можно узнать, зная эти числа (сколько всег о и на сколько больше или меньше одно число, чем другое). Далее дети формулируют задачу сначала с одним вопросом и реш ают её, затем с другим и выполняют её решение.

Выполняя задание № 3 (с. 32), дети читают каждое выраже ние, замечая, что к числу 36 прибавили это же число, умень шенное на 8 или увеличенное на 8. Можно подсказать детям, с какой величиной им надо составить задачу, например: составить задачу, в которой дана масса овощей. Далее ученики формули руют каждую задачу и устно решают её.

Задание № 3 (с. 33) дети могут выполнить самостоятельно дома, а в классе при проверке они расскажут условие своей за дачи и её решение.

На каждом из рассматриваемых уроков даны задания геом етрического содержания. В задаче на полях с. 31 требуется найти среди данных фигур лишнюю и дать три способа решения.

I           способ. Учитель предлагает назвать каждую фигуру. Дети объясняют: здесь есть треугольник, а остальные фигуры — чет ырёхугольники, значит, треугольник лишний, так как без него останутся только четырёхугольники.

II         способ. Учитель предлагает найти тупые углы в каждой из фигур и назвать их количество. Дети определяют, что в четырёху гольниках № 1 и № 3 по два тупых угла, в четырёхугольнике № 4 один тупой угол, а в треугольнике тупых углов нет. Значит, он и будет лишним.

III       способ. Четырёхугольник № 3 зелёного цвета, а остальн ые фигуры розового, значит, лишним будет четырёхуголь ник № 3.

В задаче на полях с. 30 требуется начертить данные фигуры, вырезать и составить из них: 1) один треугольник; 2) один прямоугольник.

Решение:

На полях с. 33 даны два четырёхугольника и один треуголь ник, требуется дополнить эти фигуры до прямо-угольников и, не вычисляя, сказать, периметр какого прямоугольника самый боль шой и почему.

Учитель предлагает назвать каждую фигуру и узнать, есть ли у них прямые углы. Дети находят, что в первом четырёхугольни ке два прямых угла и его легко дополнить до прямоугольника треугольником, у которого есть прямой угол (рис. 1). Во втором четырёхугольнике нет прямых углов, но его можно дополнить до прямоугольника двумя треугольниками, имеющими прямой угол (рис. 2). Треугольник можно дополнить до прямоугольника таким же треугольником (рис. 3).

Далее учитель предлагает сравнить длины сторон этих прямоу гольников. Дети находят, что длина одной из сторон этих трёх прямоугольников одинаковая, а длина другой стороны больше всех у первого прямоугольника, значит, его периметр будет самым большим.

В задачах № 1, 2  (с. 33) требуется найти периметр прямоугольника. В это время, до ознакомления с действием умн ожения, дети находят периметр прямоугольника сложением длин четырёх его сторон. Позднее они познакомятся с другими способ ами.

После чтения задачи № 1 учитель спрашивает: «Что вам изв естно о сторонах прямоугольника? (Противоположные стороны прямоугольника равны.) Если известно, что длина одной сторо ны прямоугольника 3 см, то какой длины будет противополож ная ей сторона? (3 см.) Если длина другой стороны 6 см, то какой длины будет противоположная ей сторона? (6 см.) Назо вите длину каждой из четырёх сторон этого прямоугольника. (3 см, 6 см, 3 см, 6 см или 3 см, 3 см, 6 см, 6 см.) Как узнать длины всех четырёх сторон этого прямоугольника? (Найти сумму длин всех его сторон.) Запишите решение». (3 + 6 + 3 + 6 = 18 или (3 + 3) + (6 + 6) = 18. Ответ: 18 см.)

На следующих двух уроках (с. 34, 35) надо познакомить дет ей с квадратом как с частным случаем прямо-угольника и нау чить чертить его на клетчатой бумаге.

Знакомство с понятием о квадрате можно провести так: учитель прикрепляет к доске различные прямоугольники, среди которых есть квадраты, и проводит беседу: «Какие это фигуры? (Прямоугольники.) Проверьте с помощью чертёжного треугольн ика. Найдите прямоугольники, у которых все стороны равны». Дети сначала определяют такие прямоугольники на глаз, а за тем проверяют, пользуясь линейкой. Учитель предлагает детям вспомнить, как называется прямоугольник с равными сторонами.

Для закрепления выполняются упражнения № 1, 2, 3 (1, 2) на с. 34. Чертят квадрат так же, как прямоугольник, используя разлиновку тетради в клетку. Периметр квадрата дети находят сложением длин его сторон, замечая при этом, что получается сумма одинаковых слагаемых, потому что все стороны квадрата равны.

На следующем уроке продолжается работа по закреплению знаний о квадрате: дети выполняют упражнение № 1 (с. 35). Особый интерес представляет упражнение № 1 (2): сравнив фиг уры 1 и 2, дети говорят, что обе эти фигуры — прямоугольник и, у каждой из них все углы прямые, но в фигуре 1 не все стороны равны, а в фигуре 2 все стороны равны, это квадрат; сравнив фигуры 2 и 3, дети говорят, что обе эти фигуры — ква драты, так как в каждой из них стороны равны, а углы прямые; сравнив фигуры 3 и 4, дети находят, что у каждой из них стор оны равны, но углы у фигуры 3 прямые, а у фигуры 4 не прямые.

Можно предложить детям найти в классной комнате предмет ы квадратной формы (такие предметы учитель может специальн о подготовить, например кубики, картину в квадратной рамке и т. п.).

Для закрепления ранее изученного материала в эти уроки включаются: 1) упражнения на закрепление письменных приёмов сложения и вычитания двузначных чисел (с. 34, № 4; с. 35, № 4; 2) упражнения на закрепление приёмов устных вы числений и правил порядка выполнения арифме-тических действ ий (с. 34, № 5; с. 35, № 5, 6); 3) текстовые арифметические задачи с полным текстом и в виде краткой записи или выражен ия, которое является решением задачи (с. 34, № 6; с. 35, № 2, 3); 4) уравнения (с. 34, № 7).

На каждом из рассмотренных уроков предлагаются задания на смекалку. На полях с. 34 даны числовые ребусы, которые отлич аются от ранее рассмотренных тем, что надо найти неизвестные цифры в записи не только компонентов действий, но и резуль татов.

В первом ребусе надо найти число единиц во втором слагаем ом и число десятков в сумме. Ученик рассуждает: «Подумаю, сколько единиц надо прибавить к 0 ед., чтобы получилось 5 ед.; надо прибавить 5 ед., значит, второе слагаемое — 25. Теперь узнаю число десятков в сумме: 6 + 2 = 8, значит, в сумме будет число 85. Проверю:

60 + 25 = 85».

Во втором ребусе надо узнать число десятков вычитаемого и число единиц в разности. Ученик рассуждает: «Из 4 ед. нельзя вычесть 6 ед., беру из 8 дес. 1 дес., остаётся 7 дес.; 1 дес. и 4 ед. — это 14, вычту 6 из 14, получится 8 ед., значит, разн ость равна 48; подумаю, сколько десятков надо вычесть из 7 дес., чтобы получилось 4 дес. Это 3 дес., значит, вычитаемое равно 36».

На полях с. 35 дано задание на сравнение двух сумм, в кажд ой из которых 4 слагаемых: 8 + 7 + 15 + 65 и 7 + 65 + 20 + 8, при этом требуется, не вычисляя их значений, сказать, какая из сумм больше. Дети замечают, что в суммах есть одинаковые слаг аемые: 8, 7 и 65, значит, достаточно сравнить неравные слагае мые 15 и 20: 20 > 15, следовательно, вторая сумма больше, чем первая.

На с. 40—45 даны упражнения для закрепления. Их можно использовать на уроках как дополнительный материал, а также для проверки знаний учащихся, включая в самостоятельные и контрольные работы.

Умножение и деление

По окончании работы над темой дети овладеют следующими знаниями, умениями и навыками:

•         поймут конкретный смысл действий умножения и делен ия, узнают названия компонентов и результата каждого из этих действий, а также названия соответствующих выражений; научатся решать простейшие задачи на умножение и деление (с исполь зованием моделей — предметных картинок, схематических рисунков);

•         узнают переместительное свойство умножения и научатся применять его при вычислениях; узнают, как связаны между собой компоненты и результат действия умножения;

•         выучат наизусть табличные случаи умножения и деления с числами 2 и 3;

•         научатся умножать и делить на 1, знать приёмы умножения и деления с числом 10;

•         понимать связь между величинами: цена, количество и стои мость; уметь решать простые задачи с этими величинами;

•         научатся решать задачи в два действия на сложение и вычи тание;

•         научатся выделять в фигурах углы и называть их

(прямые, острые, тупые);

•         научатся находить периметр прямоугольника.

Наглядные пособия и дидактический материал

1.       Наборы геометрических фигур для индивидуального использ ования и для демонстрации на доске: 20 кружков, 20 квадра тов, 20 треугольников (разного цвета).

2.       Плакаты с рисунками предметов, расположенных одинако выми группами, для иллюстрации произведений.

3.       Таблицы умножения с числами 2 и 3; таблица умножения Пифагора.

4.       Плакаты, иллюстрирующие названия компонентов и резуль татов действий умножения и деления.

5.       Чертёжные угольники для индивидуального пользования и для демонстрации у доски.

6.       Плакаты с изображением геометрических фигур и наборы геометрических фигур, вырезанные из бумаги, для проведения практических работ по нахождению периметров многоугольников.

На уроках, отведённых на изучение умножения (с. 48—51), надо раскрыть конкретный смысл действия умножения: дети должны усвоить, что примеры на сложение одинаковых чисел можно заменить примерами на умножение. Они должны понять, что показывает каждое число в записи примера на умножение.

Познакомить с новым действием можно так: предложить детям обвести в тетради 5 раз по 2 клеточки и провести бесед у: «Сколько всего клеточек вы обвели? (10.) Как узнали? (2 + 2 + 2 + 2 + 2 = 10.) Запишите эту сумму. Какие слагаемые в этой сумме? (Одинаковые.) Сколько их? (5.) Примеры на слож ение одинаковых чисел можно заменить примерами на умножение. (Учитель записывает на доске, а дети — в тетрадях: 2 • 5 = 10.) Точка — знак умножения. Первое число в этой зап иси (2) показывает, какое число брали слагаемым, а второе чис ло (5) показывает, сколько одинаковых слагаемых было в сум ме. Читается этот пример так: по 2 взять 5 раз, получится 10 — или так: 2 умножить на 5, получится 10».

Для закрепления: 1) проводят аналогичную работу по рисун ку и записям в учебнике (с. 48); 2) можно использовать плакат ы, на которых даны рисунки: например, нарисованы 2 ряда игрушечных машинок по 4 в каждом ряду. «Сколько машинок в каждом ряду? (4.) Сколько рядов машинок? (2.) Скольк о всего машинок? (8.) Как узнали? (4 + 4.) Как заменить этот пример примером на умножение? Запишите. (4 • 2 = 8.) Прочит айте этот пример по-разному»; 3) на следующем уроке (с. 49) продолжается работа по раскрытию конкретного смысла дейст вия умножения. Рассмотрев рисунок к упражнению № 1, дети находят, по сколько треугольников нарисовано вместе (по 6 тре угольников). «Сколько раз нарисовано по 6 треугольников? (3 раза.) Сколько всего треугольников? (18.) Как узнали? (6 + 6 + 6 = = 18.) Какие слагаемые в этой сумме? (Одинаковые.) Сколько их? (3.) Каким примером на умножение можно заменить этот пример на сложение? (По 6 взять 3 раза, 6 умножить на 3.) Сколько получится? (18.) Запишите пример на умножен ие: 6 • 3 = 18. Что показывает число 6? число 3?» (Каждое слагаемое равно 6, таких слагаемых было 3.) Выполняя осталь ные задания этого упражнения, дети поясняют данные записи, находят пропущенные числа, объясняя, как их нашли; 4) здесь же предлагается задача на умножение (с. 49, № 2). Дети чита ют задачу, выполняют рисунок, затем решают задачу сложением (2 + 2 + 2 + 2 + 2 = 10) и заменяют пример на сложение приме ром на умножение: 2 • 5 = 10. Ответ: 10 марок.

Для закрепления ранее пройденного материала выполняю т: 1) упражнения на вычисления: письменное сложение и выч итание (с. 48, № 4; с. 49, № 6). Все эти упражнения ученики могут выполнить самостоятельно в классе и дома; 2) решение текстовых арифметических задач (с. 48, № 2, 3; с. 49, № 3, 4). Данные задачи ученики решают самостоятельно, а задания на сос тавление задач выполняют устно; 3) упражнение на постановку пропущенных знаков действий в равенствах и неравенствах (с. 48, № 6) ученики выполняют устно.

Задание на смекалку («Продолжи ряд чисел») на полях

с. 48 также выполняется устно. Учитель предлагает детям выполнить его самостоятельно и объяснить решение. Если дети затрудня ются, учитель может подсказать способ решения: «Сравните каждое число с числом, которое следует за ним, и установите закономерность полученных разностей». Дети записывают на дос ке и в тетрадях разности: 11 – 7 = 4, 14 – 11 = 3, 18 – 14 = 4, 21 – 18 = 3 — и замечают, что каждое следующее число больше предыдущего сначала на 4, потом на 3, затем снова на 4, потом на 3 и т. д. Теперь дети могут продолжить ряд: следующим будет число, на 4 большее, чем 21, — это 25; за ним следует число, на 3 большее, чем 25, — это 28 и т. д.

На следующих двух уроках (с. 50, 51) продолжается работа по раскрытию конкретного смысла умножения, здесь дети знакомятся с приёмом умножения — заменой произведения сум мой одинаковых слагаемых, а также с решением простых задач на нахождение сумм одинаковых слагаемых.

1. Учитель говорит: «Сегодня вы будете учиться находить результат примеров на умножение. Прочитайте пример: 10 • 5 (10 умножить на 5, или по 10 взять 5 раз). Объясните, что обо значает первое число в этой записи. (Какое число надо взять слагаемым.) Что обозначает второе число? (Сколько раз надо взять слагаемым первое число.) Чтобы вычислить результат, за меним этот пример на умножение примером на сложение. Что обозначает число 10? (10 надо взять слагаемым.) Что обознача ет число 5? (5 раз надо взять слагаемым число 10.) Какой при мер на сложение можно записать? (10 + 10 + 10 + 10 + 10.) Выч ислите сумму. (50.) Значит, 10 умножить на 5, получится 50.

Запись:             10 • 5                                                                   

                                   10 + 10 + 10 + 10 + 10 = 50

                              10 • 5 = 50

Для закрепления знания приёма умножения дети выполняю т упражнение № 1 (с. 50). Учитель говорит: «Прочитайте задание и объясните, как находили результат примеров на умножение». (Пример на умножение заменили примером на сло жение: число 6 взяли слагаемым 4 раза. Получилось 24, значит, 6 • 4 = 24.) Так же дети объясняют решение остальных пример ов. В заключение учитель спрашивает: «Как можно вычислить результат примера на умножение?» (Надо заменить этот пример примером на сложение и вычислить его результат, который бу дет результатом примера на умножение.) Далее учитель предл агает прочитать задание к упражнению № 2 (с. 50) и найти результат первого примера. Ученик объясняет: «Заменю пример 2 • 5 примером на сложение: 2 + 2 + 2 + 2 + + 2 = 10, значит, ум ножив 2 на 5, тоже получу 10». Решение записывают так же, как показано в упражнении № 1. Аналогично выполняется реш ение остальных примеров. При этом следует обратить вниман ие детей, что при умножении нуля на 3 и на 2 получается нуль. «Сколько получится, если 0 умножить на 10? (Нуль.) А если 0 умножить на 100? (Нуль.) Почему?» (При сложении 10 нулей или

100 нулей получится 0, значит, 0 • 10 = 0, 0 • 100 = 0.)

При выполнении упражнения № 3 дети должны дать ответ, не вычисляя значений данных выражений. Например: 8 + 8 + 8 > 8 • 2, потому что 8 • 2 — это сумма двух восьмёрок, а сле ва дана сумма трёх восьмёрок.

Выполняя упражнение № 4 (с. 50), дети сначала называют те примеры на сложение, которые нельзя заменить примерами на умножение, и объясняют почему. Затем выписывают остальн ые примеры и записывают соответствующие примеры на умножение. Например: 15 + 15 + 15 = = 45 (15 • 3 = 45). Так же нах одят результат умножения в остальных примерах.

2. На этих же уроках дети учатся решать простые текстовые арифметические задачи на нахождение суммы одинаковых слагае мых (с. 50, № 5, 6; с. 51, № 1, 2). При решении каждой из этих задач полезно обратиться к Памятке: дети рассказыва ют, как они представляют содержание задачи, выполняют схема тический рисунок или чертёж, объясняют, что в задаче даны оди наковые числа, называют, сколько их, после чего решают зада чу сложением и записывают ответ, затем заменяют сложение умножением и записывают ответ. В упражнении № 1 (с. 51) показано, как можно оформить решение.

Решение задач на нахождение периметра квадрата (с. 50, № 6) выполняется так же, как и решение других задач: сначал а дети находят сумму длин сторон квадрата, затем сложение за меняют умножением.

Остальные упражнения способствуют закреплению ранее изученного материала и могут быть предложены детям для самостоятельного выполнения.

Рассмотрим упражнения с орнаментами на полях (с. 49, 51). Учителю надо спросить, из каких фигур они составлены, выяс нить, в каком порядке следуют геометрические фигуры в орнам енте, предложить продолжить черчение орнамента (так, на с. 49 далее будут следовать 1 квадрат, 1 прямоугольник, 2 ква драта и т. д.).

Ранее ученики уже находили периметр прямоугольника, вы числяя сумму длин всех его сторон. Теперь (с. 52) они знако мятся с другими способами нахождения периметра прямоугольн ика, используя действие умножения.

Эта работа проводится под руководством учителя.

Учитель говорит: «Прочитайте задание к упражнению № 1 (с. 52). Сколько сторон прямоугольника достаточно измерить? (Две.) Почему? (Длины противоположных сторон будут такими же: 2 см и 5 см.) Объясните, как находили периметр прямоу гольника первым способом. (Нашли сумму длин всех сторон: 2 + 5 + 2 + 5 = 14. Ответ: 14 см.) Рассмотрите и объясните реш ение вторым способом. (В первой сумме есть две пары одинак овых слагаемых: 2 и 2 и ещё 5 и 5, потому что противоположн ые стороны прямоугольника равны. Сложение одинаковых чис ел можно заменить умножением: (2 • 2) + (5 • 2); 2 • 2 — это сумма двух меньших сторон, а 5 • 2 — это сумма двух больших сторон, получится 4 + 10 = 14. Ответ: 14 см.) Как объяснить третий способ решения? (В сумме четырёх слагаемых 2 раза надо взять сумму 2 + 5, значит, периметр прямоугольника равен (2 + 5) • 2 = 7 • 2. Ответ: 14 см.) Как можно объяснить третий способ по чертежу?» (Сумму большей и меньшей сторон прямо угольника надо взять 2 раза, значит, периметр равен (2 + 5) • 2 = 14. Ответ: 14 см.)

Для закрепления умения по-разному находить периметр прям оугольника ученики выполняют упражнение № 2 (с. 52). Учи тель предлагает найти периметр любым способом, затем вызванн ый ученик записывает и объясняет своё решение на доске. Те ученики, которые решили задачу другим способом, записывают своё решение на доске, а остальные — в тетрадях.

Упражнения № 3—8 (с. 52) предназначены для закрепления ранее пройденного материала, и их дети могут выполнить са мостоятельно дома или в классе.

В упражнении на полях (с. 52) требуется вычленить из дан ных фигур новые (прямоугольник и 2 треугольника), проведя в каждой фигуре по два отрезка.

Учитель может начертить на доске или на листе бумаги фи гуры, подобные данным. Пусть сначала дети предложат свои реш ения. Если же они не справятся с этой задачей, учителю надо помочь наводящими вопросами. Например: «Если должен обра зоваться прямоугольник, значит, у него все углы будут прямыми. Поищите, нет ли в этих фигурах прямых углов. (У треугольника один угол прямой.) Как провести в треугольнике отрезки, чтобы образовались ещё прямые углы? (Надо, используя разлиновку тетради в клеточку, провести отрезки, которые образуют прямые углы со сторонами прямого угла треугольника.) Покажите на чертеже, какие получились прямоугольник и 2 треугольника» (рис. 1).

Чтобы получить прямоугольник и 2 треугольника в данных четырёхугольниках, надо провести отрезки от вершин углов че тырёхугольника к противоположной стороне так, чтобы каждый отрезок с противоположной стороной образовал прямой угол. При черчении прямого угла пользуются разлиновкой тетради в кле точку (рис. 2, 3).

Рис. 2

На предыдущих уроках при раскрытии конкретного смысла действия умножения дети уже находили сложением результат умножения чисел 1 и 0 на любые другие числа. На этом уро ке они должны сформулировать выводы, которые в дальнейшем станут приёмами умножения чисел 1 и 0 на любые другие числа.

При ознакомлении с приёмами умножения 1 и 0 на любые числа можно воспользоваться иллюстрацией и записями к зада че на с. 53. Прочитав задачу, дети объясняют данное решение сложением и от сложения переходят к умножению. (1 + 1 + 1 + 1 + 1 = 5, 1 • 5 = 5. Ответ: 5 всадников.)

Так же поступают при решении второй задачи. (На каждой из четырёх тарелок осталось по 0 сосисок, а всего 0 + 0 + 0 + 0 = 0, или 0 • 4 = 0. Ответ: 0 сосисок.)

Выполняя упражнение № 1, дети в каждом случае сравниваю т данные числа с полученным результатом и делают частные выводы. Например: 1 • 3 = 1 + 1 + 1 = 3, 1 • 3 = 3. Умножали 1 на 3, и получилось 3, т. е. получилось то число, на которое умно жали. 0 • 2 = 0 + 0, 0 • 2 = 0, при умножении 0 на 2 в резуль тате получится 0 и т. д.

Теперь дети могут сформулировать общие выводы:

1.       При умножении 1 на любое число в результате получится то число, на которое умножали.

2.       При умножении нуля на любое число получается нуль.

Далее можно предложить детям привести свои примеры на умножение 1 и 0 на любое число.

Для закрепления знания рассмотренных приёмов выполняют упражнение № 3 (1-й и 2-й столбики) и упражнение № 4 (1-й столбик). Выполнив упражнение № 4 (2-й столбик), надо сравнить результат умножения двух чисел с результатом сложе ния тех же чисел.

Можно также предложить решить задачу: «Найдите устно периметр квадрата, длина стороны которого 1 м; 1 дм; 1 см; 1 мм».

При выполнении упражнения, которое дано на полях с. 53, сначала учитель спрашивает: «Какие фигуры надо дополнять? (Треугольник и два четырёхугольника.) Какая фигура должна по лучиться? (Квадрат.) Что вы знаете о квадрате? (У него все сто роны равны и все углы прямые.) Начнём дополнять с треуголь ника. Есть ли в нём прямые углы? (Один угол прямой.) Нет ли равных сторон? (Две стороны равны, они по 2 см.) Подумайте и объясните, как провести по клеточкам ещё две стороны. (От вершин острых углов провести отрезки по 2 см: один сверх у вниз, другой слева направо.) Проверьте, используя чертёжный треугольник, будут ли все углы прямые». (Да, ещё три угла пря мые.)

Примерно в таком же плане выполняются задания, в которых требуется дополнить четырёхугольники до квадратов.

На следующих двух уроках (с. 54, 55) ученики знакомятся с названиями чисел и соответствующего выражения при умнож ении, учатся использовать эти термины при выполнении раз личных упражнений. Вместе с тем ведётся подготовительная раб ота к ознакомлению с переместительным свойством умножения, а также к составлению в дальнейшем таблиц умножения, закреп ляются знания ранее пройденного материала.

Знакомство с новыми терминами можно провести так: учи тель предлагает детям записать пример (3 умножить на 5), выч ислить устно результат, выполнив сложение. Учитель говорит: «Узнайте по учебнику, как называются числа при умножении». Дети читают по учебнику: «Числа, которые умножают, называются множителями (3 — пер вый множитель, 5 — второй множитель); выражение 3 • 5 называется произведением; результат умножения называется значением произведения или кратко произведением (15 — произведение)».

Для закрепления знаний следует прочитать текст в учебнике. Дети несколько раз повторяют термины. Полезно вывесить в классе плакат с названиями компонентов и результата действия умножения и соответствующего выражения (аналогично тому, как это сделано в учебнике).

Далее можно выполнить упражнение № 1 (с. 54) под руко водством учителя, в каждом случае ученики находят результат, заменяя произведение суммой (теперь дети должны пользоватьс я этими терминами). При выполнении упражнения № 2 (с. 54) дети также заменяют произведение 8 • 2 суммой и получают сумм у двух восьмёрок, а сумма трёх восьмёрок (слева) больше сумм ы двух восьмёрок.

На следующем уроке продолжается работа по закреплению знания названий чисел и соответствующего выражения при умножении. Выполняя упражнение № 1 (с. 55), дети под руков одством учителя объясняют, что записано в каждой строке таб лицы, как найти значение произведения. Вычислив произведение 2 • 6, объясняют, как вычислить произведение 2 • 7 (прибавить 2 к 12), узнав, что 3 • 2 = 6, объясняют, как проще вычислить произведение 3 • 3 (прибавить 3 к 6), и т. д.

Упражнение № 2 (с. 55) — подготовительное к составлению таблиц умножения. Дети читают задание, называют значение пер вого выражения и объясняют, как его нашли (9 + 9 = 18), затем читают выражение, записанное под первым, и объясняют, как проще найти его значение. (Надо к 18 прибавить 9, потому что в первом выражении 2 девятки, а во втором — 3, на 1 дев ятку больше.) Значит, значение второго выражения 27. Так же рассуждают при нахождении значений выражений во 2-м и 3-м столбиках.

Упражнение № 4 готовит детей к ознакомлению с приёмом перестановки множителей.

Знание переместительного свойства умножения (с. 56, 57) не только является самостоятельным вопросом, но и практически используется для нахождения произведения тогда, когда перестановка множителей помогает облегчить вычисления: удобнее боль шее число умножать на меньшее, если результат умножения на ходится сложением (легче 8 • 2, чем 2 • 8). При ознакомлении с переместительным свойством умноже ния учитель может руководствоваться методическим приёмом, предложенным в учебнике. Суть его состоит в том, что учащиес я находят значения произведений, различающихся порядком мно жителей, опираясь на иллюстрации. Иллюстрации убедительно показывают детям, что общее число изображённых кружков не изменяется при разных способах подсчёта. Например, по рисунк у 2 на с. 56 можно записать произведение 4 • 3 (3 ряда кружк ов, по 4 в каждом) и найти результат сложением — 12 круж ков. А можно вести подсчёт иначе: 3 • 4 (4 столбика кружков, по 3 в каждом, всего 12 кружков). Затем под руководством учит еля дети сравнивают значения выражений, сами выражения и делают вывод, что от перестановки множителей результат умножения не изменяется. Далее этот вывод применяется при нахождении знач ений числовых выражений без опоры на иллюстрации (с. 56, № 1; с. 57, № 2 и др.).

На следующих уроках (с. 58, 59) раскрывается конкретный смысл действия деление в процессе выполнения детьми практич еских операций с предметами, а также при решении задач на деление по содержанию и деление на равные части. На одном из уроков закрепления вводятся названия чисел при делении, а такж е название выражения.

Ознакомить с действием деления можно, предложив детям реш ить практически задачу: «Надо раздать 8 тетрадей ученикам, по 2 тетради каждому. Узнайте, сколько учеников получат тетради». Вызванный ученик берёт по 2 тетради и раздаёт их ученикам. «Сколько раз по 2 тетради он взял из всех 8 тетрадей? Сколь ко учеников получили тетради?» Учитель поясняет: «Такие задач и, в которых надо раздать (разложить, разделить) общее число предметов поровну — по 2, по 3, по 5 предметов, решают с по мощью нового действия — деления».

Опираясь на схематический рисунок, учитель записывает и чи тает решение, показывает знак деления и предлагает прочитать запись нескольким ученикам.

Для закрепления темы читают и разбирают текст на с. 58 учебника, а также решают задачу № 1 с опорой на схематиче ский рисунок.

На следующем уроке аналогичная работа проводится при ре шении задачи № 2 (с. 59). Кроме того, предлагают задачи, где деление нацело невыполнимо (т. е. при делении получается ост аток). Такие задачи необходимо изредка включать и в дальнейш ем (пока без записи решения). Это помогает сформировать пон ятие о действии деления целых положительных чисел и подго тавливает детей к изучению деления с остатком в 3 классе.

Опираясь на иллюстрации (с. 59, № 1), составляют и решаю т примеры на деление (сколько раз в 6 квадратах содержится по 2 квадрата? по 3 квадрата?).

На следующем уроке надо показать, что делением решают и такие задачи, в которых несколько предметов раздают (расклад ывают, делят) поровну, а узнать нужно, сколько предметов в каждой из равных частей. С этой целью можно предложить практ ически решить такую, например, задачу: «Надо раздать 12 тет радей поровну четырём ученикам. Узнайте, сколько тетрадей по лучит каждый ученик». К доске вызывают четырёх учеников, ещё один ученик решает задачу практически под руководством учител я. «Возьми из всех 12 тетрадей столько, чтобы дать каждому по 1 тетради. Сколько надо взять тетрадей? Ещё раз возьми 4 тетради и раздай их по 1 тетради. И ещё раз возьми 4 тетрад и и раздай по 1 тетради. Сколько тетрадей получил каждый учен ик? Сколько раз брали по 4 тетради из 12 тетрадей? Значит, каждый ученик получил столько тетрадей, сколько раз по 4 те тради содержится в 12 тетрадях. Вы знаете, что такие задачи ре шаются делением».

Решение задачи записывают так: 12 : 4 = 3; читают запись так: 12 разделить на 4, получится 3; формулиру ют ответ: каждый ученик получит 3 тетради.

Для закрепления читают текст на с. 60 и с опорой на схема тический рисунок решают задачу № 1. На следующем уроке так же рассматривают задачи из задания № 2 (с. 61). К первой за даче можно выставить на наборном полотне 15 кружков и про вести работу, иллюстрируя деление на 3 равные части: берём 3 кружка и расставляем по одному в каждый из трёх рядов наб орного полотна, берём следующие 3 и снова расставляем по одному и т. д. Сколько кружков получилось в каждом ряду? Скольк о раз по 3 кружка содержится в 15 кружках?

Решение второй задачи из задания № 2 дети могут легко прои ллюстрировать сами в тетрадях: 16 фишек (точек, кружков, треу гольников) разбивают дугами или вертикальными отрезками по 2 фишки и подсчитывают число получившихся пар.

Кроме того, опираясь на рисунок, дети решают примеры на деление (с. 61, № 1). При этом надо формулировать задания по-разному:

— Положи карандаш так, чтобы отделить 6 кружков. 

Сколько раз по 2 кружка содержится в 6 кружках?

— Отдели карандашом 8 кружков. Посмотри внима- тельно: горизонтальная линия делит их на 2 равные части. Сколько кружк ов в каждой части?

На следующем уроке учащиеся знакомятся с названиями чис ел и выражения при делении (с. 62). Методика работы над тер минологией знакома учителю. Дети узнают названия либо по учебн ику, либо по таблице — демонстрационному пособию, которое на длительное время вывешивается в классе. Далее надо следить за тем, чтобы дети активно использовали терминологию. Основная цель данного урока — решая задачи на деление по содерж анию и на равные части с одинаковыми числами, показать, что в решении задачи результаты получаются одинаковыми, хотя ил люстрации (схемы) к каждой задаче будут различаться; различ ным будет и смысл ответа в задачах.

Используя материал, данный на с. 63, 66—70, на уроках закрепл ения следует решать в сопоставлении задачи, раскрывающие конкретный смысл умножения и деления. На каждом уроке, отведённом делению, необходимо закрепить умение находить произведения разными способами (с. 62, № 7; с. 63, № 1—3 и др.), навыки устного и письменного сложения и вычитания, а также умения решать задачи в два действия. Разнообразить ра боту детей на уроках поможет включение упражнений с геомет рическим материалом: измерение и построение отрезков, распо знавание видов углов в многоугольниках, нахождение периметра прямоугольника (в том числе квадрата).

Для того чтобы дети могли находить результаты деления на основе знания соответствующих случаев умножения, необходимо ознакомить их со связью между произведением и множителям и (с. 72—74). С этой целью можно предложить учащимся расс мотреть рисунки и примеры, составленные по этим рисункам (с. 72). Вспомнив названия чисел при умножении, дети читают примеры на деление, используя терминологию действия умножен ия: произведение 8 делим на первый множитель 4, получаем второй множитель 2 (аналогично читают следующий пример). На основе этих частных выводов ученики делают общий вывод свои ми словами или читают по учебнику. Для закрепления знания связи выполняют задания № 1 и 2 (с. 72). Аналогичные упраж нения выполняют на следующем уроке (с. 73). Важно, чтобы дети не только называли ответы, но и приводили пояснения: «Произведение чисел 4 и 3 равно 12; делю произведение 12 на первый множитель 4, получаю второй множитель 3; делю прои зведение 12 на второй множитель 3, получаю первый множитель 4».

Тема следующего урока «Приёмы умножения и деления на 10» (с. 74). Здесь применяются знания конкретного смысла и переместительного свойства умножения, а также связи между произведением и множителями. Для подготовки можно решить четвёрку примеров: 6 • 2, 2 • 6, 12 : 6, 12 : 2 (с объяснением, как получен каждый следующий пример из предыдущего).

Прочитав в учебнике объяснения (с. 74), учащиеся выполняю т задание № 1: сначала составляют и решают 1-й столбик (до случая 10 • 10), где результаты находят на основе конкретно го смысла умножения; затем решают примеры 2-го столбика, используя приём перестановки множителей; результаты деления в 3-м и 4-м столбиках находят путём деления произведения на один из множителей. Часть примеров решают с пояс нением вслух, часть — самостоятельно с пояснением про себя.

На уроках закрепления случаи умножения и деления с числ ом 10 включаются как в примеры, так и в задачи (с. 74, № 3; с. 75, № 2; с. 76, № 2).

Кроме того, на этих уроках дети решают задачи с величина ми: цена, количество, стоимость (с. 72, № 3; с. 73, № 3 и др.). Заметим, что в задачах используется только термин «цена» как наиболее известный детям, названия других величин и связи межд у ними будут изучаться в 3 классе. Например: «Цена тетради 3 р. Сколько стоят 5 таких тетрадей?» (с. 73, № 3). Сделав схематический рисунок (нарисовав 5 кружочков и рядом с кажд ым записав 3 р.), дети отвечают на вопрос задачи, опираясь на конкретный смысл умножения (надо число 3 взять слагаемым 5 раз, т. е. 3 умножить на 5). Затем составляют обратные зада чи, например: «За 5 одинаковых тетрадей заплатили 15 р. Скольк о стоит одна тетрадь?» Чтобы ответить на вопрос задачи, надо произведение 15 разделить на один из множителей — 5, получает ся другой множитель — 3. Значит, ответ задачи: цена тетра ди 3 р.

Специальный урок отводится для рассмотрения задач на нах ождение третьего слагаемого, когда известна сумма трёх слага емых и два из них (с. 76).

К решению задач этого вида дети достаточно подготовлены: они решали много простых задач на нахождение неизвестного слагаемого, а также решали составные задачи на вычитание сумм ы из числа. Если учитель сочтёт необходимым, можно на подг отовительном этапе напомнить детям, включив такие задачи, нап ример, в устный счёт. При этом задачу на вычитание суммы из числа полезно решить разными способами.

В учебнике на с. 76 приведены задачи данного вида. К обеи м задачам дано несколько выражений, смысл которых должны объяснить дети. Поэтому решение этих задач разными способам и не вызывает особых затруднений у учащихся. При решении задачи № 2 целесообразно использовать чертёж. Заметим: так как детям знакомо сложение отрезков, то более удачным надо считать изображение суммы трёх слагаемых одним отрезком, на котором отмечены как известные слагаемые, так и искомое слаг аемое. Это замечание относится также и к другим задачам, вклю чённым в учебник (с. 77, № 4; с. 78, № 4 и др.).

Главная задача при изучении материала следующих уроков (с. 80—101) — составить вместе с детьми таблицы умножения и деления, выполнить различные упражнения, способствующие прочному запоминанию этих таблиц. Вместе с тем на основе изу ченных знаний об умножении и делении рассматриваются разл ичные приёмы нахождения табличных результатов, которыми учащ иеся могут воспользоваться в случае забывания какого-то результата.

При рассмотрении этой темы можно выделить две подтемы: таблицы умножения и деления с числом 2 (умножение числа 2, умножение на 2, деление на 2); затем в таком же порядке изу чаются таблицы с числом 3. На каждом из этих этапов включ ается достаточное число уроков на закрепление изученного.

Таблица умножения с числом 2 (всего 8 случаев) рассматри вается на двух уроках (с. 80, 81). При ознакомлении с таблиц ей первые 4 случая можно записать на доске и предложить уча щимся прочитать их. Учитель поясняет: «Вычислив результаты этих примеров, мы получим таблицу умножения числа 2, кото рую надо запомнить».

Результаты находят, заменяя умножение сложением, опираясь на соответствующую иллюстрацию и сумму нескольких одинаков ых слагаемых, каждое из которых равно 2 (с. 80). Дети запис ывают и читают таблицу: 2 умножить на 2, получится 4; 2 умн ожить на 3, получится 6 и т. д. Для закрепления проводится работа по учебнику. Так как легче запоминать таблицу умножен ия, когда постоянным является второй множитель (её можно читать коротко, со словом «дважды»), то учитель предлагает детям, применив перестановку множителей, записать таблицу умн ожения на 2 и постараться её запомнить. Показывают приёмы запоминания: чтение (краткое) вслух и про себя; воспроизведен ие таблицы, когда закрыты результаты или, наоборот, закрыты выражения; воспроизведение табличных случаев подряд или враз бивку и т. п.

Для первичного закрепления предлагаются упражнения № 1, 2 (с. 80). Аналогично проводится работа над второй частью таблицы на следующем уроке (с. 81).

На уроке закрепления особое внимание уделяют разным спос обам вычисления табличных результатов в случае их забывания. Это не только замена умножения сложением, но и использован ие других случаев из таблицы, которые хорошо известны (с. 82). Чтобы дети смогли воспользоваться различными приёмами вы числений на данном уроке и в дальнейшем, надо включить уп ражнения на применение таких приёмов (с. 82, № 1).

Составление таблицы деления на 2 тоже является способом закрепления таблицы умножения. Прежде всего, опираясь на ил люстрации, учитель повторяет с детьми связь между произведе нием и множителями (с. 83, № 1). По каждому примеру на умн ожение составляют и записывают два примера на деление. Учит ель обращает внимание детей на запоминание соответствующих троек чисел (иногда их называют «тройками дружных чисел»).

Далее отводится несколько уроков на закрепление всех расс мотренных таблиц с числом 2 (с. 84, 87). В учебнике даны разн ообразные упражнения: решение примеров в одно и несколько действий, решение задач, нахождение значений буквенных выраж ений, сравнение выражений и др. Полезно также использовать игровые и занимательные упражнения: решить круговые примеры, пройти лабиринт, продолжить ряд чисел, составленный по определённому правилу, поработать на Вычислительной машине и т. п.

Методика работы над таблицами умножения и деления с чис лом 3 (с. 90—99) аналогична выше рассмотренной. Однако, учит ывая накопленный детьми опыт, следует предоставлять им больш е самостоятельности. Несмотря на то что основное внимание уделяется на этих уроках новым таблицам, необходимо системат ически включать табличные случаи с числом 2.

Последние 8—10 уроков отводятся повторению основных вопросов из пройденного (с. 102—111). Материал в учебнике изложен по темам: нумерация; выражения, равенства, неравенс тва, уравнения; сложение и вычитание; решение задач; длина отрезка, единицы длины; геометрические фигуры. Планируя ра боту на уроках, учитель уделяет больше внимания тем вопросам, которые, по его мнению, усвоены детьми недостаточно. Разуме ется, на каждом уроке по-прежнему закрепляют знание таблиц сложения и вычитания, таблиц умножения и деления, а также умение решать задачи. Для проверки оценки знаний и умений в учебнике даны тесты (с. 100—101), а также разноуровневые контрольные работы (с. 110—111).

Тексты контрольных работ, составленные в соответствии с требованиями программы по математике, также представлены в пособии для учителя «Математика. 1—4 классы. Контрольные работы» автора С. И. Волковой (2 класс).

ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ (ПРЕДМЕТНЫЕ, ЛИЧНОСТНЫЕ, МЕТАПРЕДМЕТНЫЕ) ПО ИТОГАМ ОБУЧЕНИЯ ВО 2 КЛАССЕ^[5]

Личностные результаты

У учащегося будут сформированы:

•         понимание того, что одна и та же математическая модель отражает одни и те же отношения между различными объектами;

•         элементарные умения в проведении самоконтроля и самооценки результатов своей учебной деятельности (поурочно и по результатам изучения темы);

•         элементарные умения самостоятельного выполнения работ и осознание личной ответственности за проделанную работу;

•         элементарные правила общения (знание правил общения и их применение);

•         начальные представления об основах гражданской идентичности (через систему определённых заданий и упражнений);

•         уважение семейных ценностей, понимание необходимости бережного отношения к природе, к своему здоровью и здоровью других людей.

Учащийся получит возможность для формирования:

•         интереса к отражению математическими способами отношений между различными объектами окружающего мира;

•         первичного (на практическом уровне) понимания значения математических знаний в жизни человека и первоначальных умений решать практические задачи с использованием математических знаний;

•         потребности в проведении самоконтроля и в оценке результатов учебной деятельности.

Метапредметные результаты

РЕГУЛЯТИВНЫЕ

Учащийся научится:

•         понимать, принимать и сохранять учебную задачу и решать её в сотрудничестве с учителем в коллективной деятельности;

•         составлять под руководством учителя план действий для решения учебных задач;

•         выполнять план действий и проводить пошаговый контроль его выполнения в сотрудничестве с учителем и одноклассниками;

•         в сотрудничестве с учителем находить несколько способов решения учебной задачи, выбирать наиболее рациональный.

Учащийся получит возможность научиться:

•         принимать учебную задачу, предлагать возможные способы её решения, воспринимать и оценивать предложения других учеников по её решению;

•         оценивать правильность выполнения действий по решению учебной задачи и вносить необходимые исправления;

•         выполнять учебные действия в устной и письменной форме, использовать математические термины, символы и знаки;

•         контролировать ход совместной работы и оказывать помощь товарищу в случаях затруднений.*

ПОЗНАВАТЕЛЬНЫЕ Учащийся научится:

•         строить несложные модели математических понятий и отношений, ситуаций, описанных в задачах;

•         описывать результаты учебных действий, используя математические термины и записи;

•         понимать, что одна и та же математическая модель отражает одни и те же отношения между различными объектами;

•         иметь общее представление о базовых межпредметных понятиях: числе, величине, геометрической фигуре;

•         применять полученные знания в изменённых условиях;

•         осваивать способы решения задач творческого и поискового характера; выполнять сравнение, обобщение, классификацию заданных объектов;

•         выделять из предложенного текста информацию, дополнять ею текст задачи с недостающими данными, составлять по ней текстовые задачи с разными вопросами и решать их;

•         осуществлять поиск нужной информации в материале учебника и в других источниках (книги, аудио- и видеоносители, а также Интернет с помощью взрослых);

•         представлять собранную в результате расширенного поиска информацию в разной форме (пересказ, текст, таблицы).

Учащийся получит возможность научиться:

•         фиксировать математические отношения между объектами и группами объектов в знаково-символической форме (на моделях);

•         осуществлять расширенный поиск нужной информации в различных источниках, использовать её для решения задач, математических сообщений, изготовления объектов с использованием свойств геометрических фигур;

•         анализировать и систематизировать собранную информацию и представлять её в предложенной форме (пересказ, текст, таблица).

КОММУНИКАТИВНЫЕ Учащийся научится:

•         строить речевое высказывание в устной форме, использовать математическую терминологию;

•         оценивать различные подходы и точки зрения на обсуждаемый вопрос;

•         уважительно вести диалог с товарищами, стремиться к тому, чтобы учитывать разные мнения;

•         принимать активное участие в работе в паре и в группе с одноклассниками: определять общие цели работы, намечать способы их достижения, распределять роли в совместной деятельности, анализировать ход и результаты проделанной работы;

•         вносить и отстаивать свои предложения по организации совместной работы, понятные для партнёра, по обсуждаемому вопросу;

•         осуществлять взаимный контроль и оказывать в сотрудничестве необходимую взаимную помощь.

Учащийся получит возможность научиться:

•         самостоятельно оценивать различные подходы и точки зрения, высказывать своё мнение, аргументированно его обосновывать;

•         контролировать ход совместной работы и оказывать помощь товарищу в случаях затруднения.¹

^* Работа на обозначенный результат будет продолжена в основной и старшей школе, а также при изучении других курсов системы учебников «Школа России».

Предметные результаты

ЧИСЛА И ВЕЛИЧИНЫ

Учащийся научится:

• образовывать, называть, читать, записывать числа от

0 до 100;

•         сравнивать числа и записывать результат сравнения;

•         упорядочивать заданные числа;

•         заменять двузначное число суммой разрядных слагаемых;

•         выполнять сложение и вычитание вида 30 + 5, 35 – 5, 35 – 30;

•         устанавливать закономерность — правило, по которому составлена числовая последовательность (увеличение/ уменьшение числа на несколько единиц); продолжать её или восстанавливать пропущенные в ней числа;

•         группировать числа по заданному или самостоятельно установленному признаку;

•         читать и записывать значения длины, используя изученные единицы измерения этой величины (миллиметр, сантиметр, дециметр, метр) и соотношения между ними: 1 м = 100 см; 1 м = 10 дм; 1 дм = 10 см; 1 см = 10 мм;

•         читать и записывать значение величины время, используя изученные единицы измерения этой величины (час, минута) и соотношение между ними: 1 ч = 60 мин; определять по часам время с точностью до минуты;

•         записывать и использовать соотношение между рублём и копейкой: 1 р. = 100 к.

Учащийся получит возможность научиться:

•         группировать объекты по разным признакам;

•         самостоятельно выбирать единицу для измерения таких величин, как длина, время, в конкретных условиях и объяснять свой выбор.

АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ Учащийся научится:

•         воспроизводить по памяти таблицу сложения чисел в пределах 20 и использовать её при выполнении действий сложения и вычитания;

•         выполнять сложение и вычитание в пределах 100: в более лёгких случаях устно, в более сложных — письменно (столбиком);

•         применять переместительное и сочетательное свойства сложения при вычислениях.

•         выполнять проверку правильности выполнения сложения и вычитания;

•         называть и обозначать действия умножения и деления;

•         заменять сумму одинаковых слагаемых произведением и произведение суммой одинаковых слагаемых;

•         умножать 1 и 0 на число; умножать и делить на 10;

•         читать и записывать числовые выражения в 2 действия;

•         находить значения числовых выражений в 2 действия, содержащих сложение и вычитание (со скобками и без скобок);

•         использовать термины уравнение, буквенное выражение.

Учащийся получит возможность научиться:

•         вычислять значение буквенного выражения, содержащего одну букву при заданном её значении;

•         решать одношаговые уравнения подбором неизвестного числа;

•         моделировать действия умножение и деление с использованием предметов, схематических рисунков и схематических чертежей;

•         раскрывать конкретный смысл действий умножение  и деление;

•         применять переместительное свойство умножения при вычислениях;

•         называть компоненты и результаты действий умножения и деления;

•         устанавливать взаимосвязи между компонентами и результатом умножения;

•         выполнять умножение и деление с числами 2 и 3.

РАБОТА С ТЕКСТОВЫМИ ЗАДАЧАМИ Учащийся научится:

•         решать задачи в 1—2 действия на сложение и вычитание, на разностное сравнение чисел и задачи в одно действие, раскрывающие конкретный смысл действий умножение и деление;

•         выполнять краткую запись задачи, схематический рисунок;

•         составлять текстовую задачу по схематическому рисунку, по краткой записи, по числовому выражению, по решению задачи.

Учащийся получит возможность научиться:

•         решать задачи, используя общий план работы над задачей, проверять решение задач указанным способом.

ПРОСТРАНСТВЕННЫЕ ОТНОШЕНИЯ. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ

Учащийся научится:

•         распознавать и называть углы разных видов: прямой, острый, тупой;

•         распознавать и называть геометрические фигуры: треугольник, четырёхугольник и др., выделять среди четырёхугольников прямоугольник (квадрат);

•         выполнять построение прямоугольника (квадрата) с заданными длинами сторон на клетчатой разлиновке с использованием линейки;

•         соотносить реальные объекты с моделями и чертежами треугольника, прямоугольника (квадрата).

Учащийся получит возможность научиться:

•         изображать прямоугольник (квадрат) на нелинованной бумаге с использованием линейки и угольника. ГЕОМЕТРИЧЕСКИЕ ВЕЛИЧИНЫ Учащийся научится:

•         читать и записывать значения длины, используя изученные единицы длины и соотношения между ними (миллиметр, сантиметр, дециметр, метр);

•         вычислять длину ломаной, состоящей из 2—5 звеньев, и периметр многоугольника (треугольника, четырёхугольника, пятиугольника).

Учащийся получит возможность научиться:

•         выбирать наиболее подходящие единицы длины в конкретной ситуации;

•         вычислять периметр прямоугольника (квадрата); • проводить логические рассуждения и делать выводы. РАБОТА С ИНФОРМАЦИЕЙ Учащийся научится:

•         читать и заполнять таблицы по результатам выполнения задания;

•         заполнять свободные клетки в несложных таблицах, определяя правило составления таблиц;

•         понимать простейшие высказывания с логическими связками: если…, то…; все; каждый и др., выделяя верные и неверные высказывания.

Учащийся получит возможность научиться:

•         самостоятельно оформлять в виде таблицы зависимости между величинами: цена, количество, стоимость.

ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ

  * Здесь и далее: задания из рубрики «Странички для любознательных» по усмотрению учителя могут быть использованы на отдельном уроке  или распределены по урокам всей темы.

** На выполнение заданий рубрики «Проверим себя и оценим свои достижения» на уроке отводится 10—12 мин.

Продолжение

Продолжение

МЕТОДИЧЕСКИЕ РАЗРАБОТКИ УРОКОВ

Развёрнутый план урока по теме

«Замена двузначного числа суммой разрядных слагаемых»

Развёрнутый план урока по теме «Длина ломаной»

Развёрнутый план урока по теме «Переместительное и сочетательное свойства сложения» (закрепление)

СОДЕРЖАНИЕ

Введение .............................................................................3

Научно-методические основы курса математики

и их реализация в УМК для 2 класса ............................4

Особенности структуры и содержания учебника ..............13 Описание содержания

и структуры учебника ................................................13

Достижение личностных

и метапредметных результатов ....................................16

Методические особенности

работы с учебником ...............................................................24

Реализация системно-деятельностного подхода ..........24

Методика работы

над дополнительным материалом учебника ...........36

Методика работы

по основным вопросам предметного содержания ......52

Планируемые результаты

(предметные, личностные, метапредметные)

по итогам обучения во 2 классе .....................................135 Личностные результаты .............................................135 Метапредметные результаты .....................................136

Предметные результаты .............................................138

Тематическое планирование ..........................................141

Методические разработки уроков ..................................147

Учебное издание

Серия «Школа России»

Волкова Светлана Ивановна

Степанова Светлана Вячеславовна

Бантова Мария Александровна

Бельтюкова Галина Васильевна

МАТЕМАТИКА

Методические рекомендации

2 класс

Учебное пособие для общеобразовательных организаций

Центр начального образования Редакция естественно-математических предметов

Руководитель Центра Ю. Е. Акимова

Заведующий редакцией О. А. Подымова Редакторы А. Е. Бойцова, И. В. Чернецова-Рождественская

Ответственный за выпуск И. В. Чернецова-Рождественская

Оператор Е. С. Максимова

Художественный редактор Е. Ю. Новикова Вёрстка В. В. Верженской

Технический редактор Н. Н. Бажанова

Корректоры И. Н. Панкова, И. В. Чернова

             Налоговая       льгота     —       Общероссийский        классификатор        продукции

ОК 005-93—953000. Изд. лиц. Серия ИД № 05824 от 12.09.01. Подписано в печать с диапозитивов 00.06.17. Формат 60  90 ¹/₁₆.

Бумага офсетная. Гарнитура Школьная. Печать офсетная. Уч.-изд. л. 000. Тираж      экз. Заказ №    .

Акционерное общество «Издательство «Просвещение». 127521, Москва, 3-й проезд Марьиной рощи, 41.

ОАО ордена «Знак Почёта» «Смоленская областная типография им. В. И. Смирнова». 214000, г. Смоленск, пр. Гагарина, 2.

Индивидуальное планирование учителя

Индивидуальное планирование учителя

Индивидуальное планирование учителя

Индивидуальное планирование учителя