Поделиться
МАТЕРИАЛ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ.doc
Свойства и графики тригонометрических функций
Функция y=sinx
Таблица значений тригонометрической функции y=sinx
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
0 |
|
|
|
1 |
|
|
|
0 |
|
|
|
-1 |
|
|
|
0 |
1 единичный отрезок = 2 клетки
π
≈ 3,14 ≈ 3=6 клеток 
=1 клетка
=1,5 клетки 
=2 клетки
=3 клетки 
=12 клеток
Постройте координатную плоскость: ось ОХ от начала и до конца страницы, ось OY - три клетки верх и три клетки вниз.
Отметьте единичный отрезок на оси OY – 2 клетки, на оси ОХ – соответствующие точки.
Проведите асимптоты графика пунктирной линией. (прямые, ограничивающие график функции)
Отметьте точки на координатной плоскости, учитывая область значений функции y=sinx: Ef=[-1;1], и постройте эскиз графика.
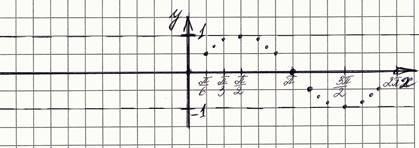
Учитывая, что sin(x+2π)=sinx (значения функции повторяются через 12 клеток) и sin(-x)=-sinx, постройте остальные элементы графика, перенеся каждую точку на 12 клеток вправо и влево
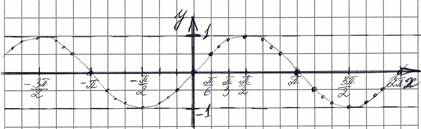
Получаем график функции y=sinx.
Свойства функции. (n
Z)
1. Область определения: Df(sin)=R
2. Область значения: Ef(sin)=[-1;1]
3. Нечетная: sin(-x)=-sinx
4. Периодичная: T=2π
5. Нули функции: OX – (πn;0) OY – (0;0)
6. Промежутки знакопостоянства:
f(x)>0 при x
(2πn; π+2πn) f(x)<0 при x
(-π+2πn; 2πn)
7. Монотонность функции
f(x) возрастает при x
[-
+2πn; 
+2πn]
f(x) убывает при x
[
+2πn; 
+2πn]
8. Экстремумы функции
(-
+2πn; -1) – точка минимума (
+2πn; 1) – точка максимума
Обратная функция
Так
как функция синус возрастает на отрезке [-
;
] и принимает все значения от -1 до
1, то для нее существует обратная: y=
arcsinx (арксинус).
Определение:
Арксинусом числа а называется такое число из отрезка [-
; 
]
, синус которого равен а.
Например:
arcsin 
=
, так как sin
=
arcsin (-
)=-
, так как sin (-
)=-
Функция y=cos x
По формулам приведения sin(x+
)=cosx. Получаем, что для построения
графика функции y=cos x достаточно произвести преобразование над графиком
функции y= sin x.
Выполним
сдвиг вдоль оси ОХ влево на 
=3 клетки.
Получаем график функции y=cosx.
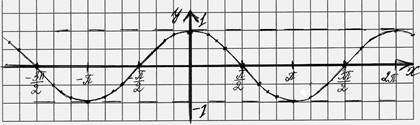
Свойства функции. (n
Z)
1. Область определения: Df(cos)=R
2. Область значения: Ef(cos)=[-1;1]
3. Четная: cos(-x)=cosx
4. Периодичная: T=2π
5. Нули
функции: OX – (
+
πn;0) OY – (0;1)
6. Промежутки знакопостоянства:
f(x)>0 при x
( -
+2πn; 
+2πn) f(x)<0 при x
(
+2πn; 
+
2πn)
7. Монотонность функции
f(x) возрастает при x
[-π+2πn; 2πn]
f(x) убывает при x
[2πn; π +2πn]
8. Экстремумы функции
(π+2πn; -1) – точка минимума (2πn; 1) – точка максимума
Обратная функция
Так как функция косинус убывает на отрезке[0; π] и принимает все значения от -1 до 1, то для нее существует обратная: y= arccosx (арккосинус).
Определение: Арккосинусом числа а называется такое число из отрезка [0; π] , косинус которого равен а.
Например:
arccos 
=
, так как cos
=
arccos (-
)=
, так как cos
=-
Функция y=tg x
Таблица значений тригонометрической функции y=tgx
|
x |
0 |
|
|
|
|
|
y |
0 |
|
1 |
|
∞ |
Проведите
асимптоты графика пунктирной линией через точки x=
(прямые, ограничивающие график
функции)
Учитывая, что tg(x+π)=tgx (значения функции повторяются через 6 клеток) и tg(-x)=-tgx, постройте график функции y=tgx.
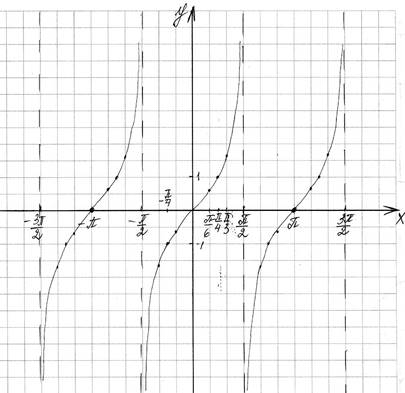
Свойства функции. (n
Z)
1.
Область определения: Df(tg)= ( -
+πn; 
+πn)
2. Область значения: Ef(tg)=R
3. Нечетная: tg(-x)=-tgx
4. Периодичная: T=π
5. Нули функции: OX – (πn;0) OY – (0;0)
6. Промежутки знакопостоянства:
f(x)>0 при x
(πn; 
+πn) f(x)<0 при x
(-
+πn; πn)
7. Монотонность функции
f(x) возрастает при x
(-
+πn; 
+πn)
8. Экстремумы функции - нет
Обратная функция
Так как
функция тангенс возрастает на отрезке (-
;
) и принимает все действительные значения
, то для нее существует обратная: y=
arctgx (арктангенс).
Определение:
Арктангенсом числа а называется такое число из отрезка (-
; 
)
, тангенс которого равен а.
Например:
arctg 1=
,
так как tg 
=1
arctg (-
)=-
, так как tg (-
)=-
Функция y=ctg x
По
формулам приведения tg(x-
)=-ctgx. Получаем, что для построения
графика функции y=ctg x достаточно произвести преобразование над графиком
функции y= tg x: сдвиг на 3 клетки вправо и преобразование симметрии
относительно оси ОХ.
Выполним
сдвиг вдоль оси ОХ вправо на 
=3 клетки,
отобразим верхнюю часть графика вниз, нижнюю – вверх (перевернем график). Получаем график функции y=ctgx.
Постройте график функции y=ctg x
Свойства функции. (n
Z)
1. Область определения: Df(ctg)= ( πn; π+πn)
2. Область значения: Ef(ctg)=R
3. Нечетная: ctg(-x)=-ctgx
4. Периодичная: T=π
5. Нули
функции: OX – (
+
πn;0) OY – нет
6. Промежутки знакопостоянства:
f(x)>0 при x
(πn; 
+πn) f(x)<0 при x
(-
+πn; πn)
7. Монотонность функции
f(x) убывает при x
(πn; π +πn)
8. Экстремумы функции – нет
Обратная функция
Так как функция котангенс убывает на отрезке(0; π) и принимает все действительные значения, то для нее существует обратная: y= arcctgx (арккотангенс).
Определение: Арккотангенсом числа а называется такое число из отрезка (0; π), котангенс которого равен а.
Например:
arcctg 
=
, так как ctg
=
arcctg (-
)=
, так как cos
=-
Преобразование графиков
|
1 |
f (x+a) |
Перенос графика y=f(x) вдоль оси ОХ (a>0 – влево, a<0 -вправо) |
|
2 |
f (x)+b |
Перенос графика y=f(x) вдоль оси ОY (b>0 – вверх, b<0 -вниз) |
|
3 |
-f (x) |
Симметрия относительно оси абсцисс |
|
4 |
f (-x) |
Симметрия относительно оси ординат |
|
5 |
|f (x)| |
Часть графика в верхней полуплоскости и на оси абсцисс без изменения, а вместо части графика в нижней полуплоскости строим ей симметричную относительно оси ОХ |
|
6 |
f (|x|) |
Часть графика в правой полуплоскости и на оси ординат без изменения, а вместо части графика в левой полуплоскости строим ей симметричную относительно оси ОY |
|
7 |
f (kx), (k>0) |
При k>1 сжатие к точке (0;0) вдоль оси абсцисс в k раз, при 0<k<1 растяжение от точки (0;0) вдоль оси абсцисс в 1/k раз |
|
8 |
k f(x), (k>0) |
При k>1 растяжение от точки (0;0) вдоль оси ординат в k раз, при 0<k<1 сжатие к точке (0;0) вдоль оси ординат в 1/k раз |
ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Постройте графики функций
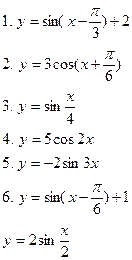
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
