Пособие по подготовке к ЕГЭ по профильной математике (задание № 11)

Затиева Ольга Викторовна

Пособие

по решению задач №11

ЕГЭ по профильной математике

2024 – 2025 уч.год

1. Графики одной функции

1.1. Линейная функция

Задание: на рисунке изображён график функции

f(x)= kx+b. Найдите значение x, при котором f(x)= -13,5

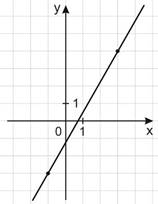
Решение 1:

1) Для начала найдем значения k и b. Данный график функции проходит через точки (3; 4) и (-1; -3). Подставим координаты наших точек в уравнение прямой y = kx + b, получим систему:

2) Для того, чтобы решить эту системы мы вычтем из первого уравнения второе:

=>

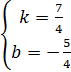
3) Получаем уравнение прямой:

4) Находим, при каком значении x значение функции равно -13,5, подставив      

y = -13,5

= -13,5

7x-5 = -54

7x = -49

x = -7

Решение 2: посмотрев на две точки которые нам даны, мы можем достроить прямоугольный треугольник. Коэффициент k равняется тангенсу угла, между прямой и положительным направлением оси OX. Таким образом тангенс угла равен , значит k=. Для нахождения b смотри пункт один из  первого решения.

Ответ: -7

1.2. Функции модуля

Задание: на рисунке изображен график функции вида f(x)=|ax+b|+c, где числа a, b и c – целые. Найдите f(88).

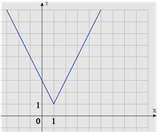
Решение1:

1) Найдем наименьшее значение функции. Оно равно 1, значит c=1.

2) f(1)=1, значит |a+b|+1=1 => a+b = 0.

3) f(0)=3, значит, |0+b|=3 =>

Эти варианты оба дают одну и ту же функцию. Можем считать, что b=2, a=-2

Для нахождения значения a, можно использовать тангенс угла наклона прямых к оси OX.

2) Получаем уравнение:

f(x)=|-2x+2|+1

3) Находим f(88):

f(88)=|-288+2|+1=175

Ответ: 175

1.3. Функция корня

         Задание: на рисунке изображен график функции вида y=+ c, где числа a, b и c – целые. Найдите f (160).

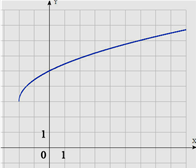
Решение:

1) Данный график на 3 сдвинут вверх относительно оси OX, значит, с=3.

f(-2)=3, значит, +3=3 => -2a+b=0

f(0)=5, значит, +3=5 => b=4, a=2

Также b можно найти другим способом. График смещен на 2 относительно оси OY влево. Значит, b==4.

2) Получаем уравнение:

y=+ 3

3) Находим f(160)= , +3=21

         Ответ: 21

1.4. Гипербола

Задание: на рисунке изображен график функции вида

y= +c, где числа a, b и c – целые. Найдите f (12).

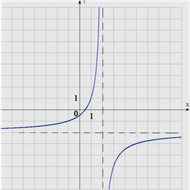
Решение:

1) Посмотрев на рисунок, мы видим, что гипербола имеет горизонтальную асимптоту y = -2, значит, c = -2. Так же, гипербола имеет вертикальную асимптоту x = 2, значит, b = -2

2) f (1)=1 ( находим с помощью точки на графике), подставляем значения в исходную формулу:

 – 2 = 1 => a=-3

3) Получаем уравнение:

y=  - 2

4)  Находим f(12):

f(12)= – 2= -2,3

         Ответ: -2,3

1.5. Квадратичная функция

Задание: на рисунке показан график функции вида f(x)=a+bx+c, где числа a, b и c – целые. Найдите f (18).

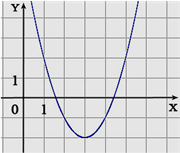
Решение 1:

1) Вершина данной параболы находится в точке x=3, значит, - = 3 => b=-6a. Значение функции при x=1, равно 2, значит, a+b+c=2. Значение функции при x=2 равно -1, значит, 4a+2b+c=-1.

2) Получаем и решаем систему:

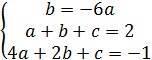
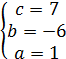
3) Получаем уравнение:

f(x)=- 2

4) Находим f (18):

f(18)= 18× 18-6 × 18+7=223

         Ответ: 223

Решение 2: по графику видно, что уравнение данной параболы

f(x)=- 2

Находим f (18):

f (18) = -2=223

Ответ: 223

1.6. Графики тригонометрических функций

Задание: на рисунке показан график функции вида f(x)=a× cos(bx)+ c, где числа a, b и c – целые. Найдите f (  ).

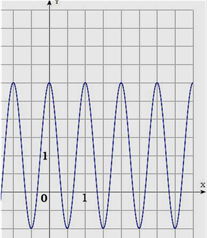
Решение:

1) По графику видно, что fmin= -1, a fmax= 3.

=1.

2) f(0)= a× cos(0)+1=3, значит, a+1=3 => a=2

3) По рисунку видно, что наименьший положительный период равен 1, значит, b=2 => b=2

4) Получаем уравнение:

f(x)=2× cos(2x)+ 1

5) Находим f (  ).

f (  )=2× cos(2)+1= 2× cos(6)+1=2× cos( )+1=

= -1+1=0

         Ответ: 0

Задание: на рисунке показан график функции вида f(x)=a× sin(bx)+c, где числа a, b и c – целые. Найдите f (  ).

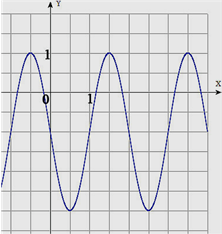
Решение: 

1) f(0)= a× sin(0)+c= -1 ó 0+c= -1, c= -1

2) По рисунку видно, что наименьший положительный период равен 2, значит:  2b=2 => b=1

3) По графику fmin= -3, a fmax=1.

=2

График в окрестности x=0 убывает => a= -2

4) Получаем уравнение:

f(x)=-2× sin(x) -1

5) Находим f (  ).

f (  )= -2× sin()-1=-2× sin(4)-1=2× sin( ) -1=0

         Ответ: 0

1.7. Показательная функция

Задание: на рисунке показан график функции вида f(x)=+c, где числа a, b и c – целые. Найдите f (3).

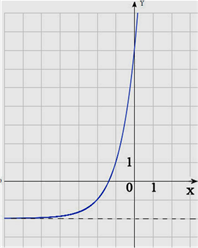
Решение:

1)Имеется асимптота y=-2, значит c=-2 (график смещен вниз на две клетки)

2) f(0)=7, значит, -2=7 =>  =9 => b=2

3) f(-1)=1, значит,  - 2=1 =>=3 => a=1

4) Получаем уравнение: 

f(x)=-2

5) Находим f (3).

f (3)= -2=241

         Ответ: 241

1.8. График логарифма

Задание: на рисунке показан график функции вида f(x)=(x+b) +c, где числа a, b и c – целые. Найдите f (510).

Решение:

1)Данный график получается из графика y=(x) сдвигом влево на 2 по оси OY, значит, b=2 и сдвигом вниз на 2 по оси OX, значит, с=-2

2) Получаем уравнение:

f(x)=(x+2) -2

3) Находим f (510).

f (510) =

         Ответ: 7

2. Графики двух функций

2.1. Парабола + прямая

Задание: на рисунке показаны графики функций g(x)= kx+b и f(x)=a+bx+c, которые пересекаются в точках А и В. Найдите абсциссу точки В.

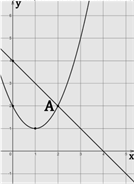
Решение:

1) Прямая проходит через точки (2;2) и (0;4). Получаем и решаем систему

Таким образом, уравнение данной прямой y= -x+4

2) Уравнение параболы имеет вид у=a+bx+с. По графику видно, что с=2. Абсцисса вершины x=1, значит, -  = 1 => b=-2a. Значение в х=1 равно 1, значит, a+b+c=1.  Получаем систему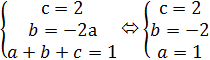

3) Уравнение параболы у=- 2x+2.

Чтобы найти пересечения графиков функций приравняем их уравнения

- 2x+2= -x+4

- x – 2=0

х1= -1

х2= 2

Абсцисса точки В это х=-1.

         Ответ: -1

2.2. Гипербола + прямая

Задание: на рисунке показаны графики функций

y= kx - 2 и y=, которые пересекаются в точках А и В. Найдите ординату точки В.

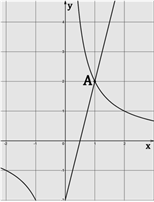
Решение:

1)  Прямая y= kx – 2 проходит через точку (1;2). Получаем уравнение 2=k-2 => k=4. Получаем уравнение данной прямой y= 4x – 2.

2) График гиперболы y= также проходит через точку (1;2). Получаем уравнение 2= => a=2.  Получаем уравнение y=

3) Для поиска пересечения графиков приравниваем их уравнения

4x – 2= ó  ó ó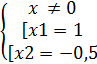

4) x=-0,5 это абсцисса точки В. Чтобы найти ее ординату, надо подставить

x=-0,5 в любую функцию которая нам дана.

y=4(-0,5) – 2= -4

         Ответ: -4

2.3. Парабола + парабола.

Задание: на рисунке показаны графики функций

f(x)=-2-2x+4 и g(x)=a+bx+c, которые пересекаются в точках А (-1;4) и В (; .

Найдите .

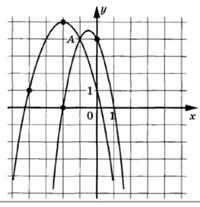
         Решение:

Для начала найдем вершину, чтобы понять уравнение какой параболы нам известно.  = - 0,5. Таким образом известная нам парабола находится правее.

1) Подставим точки c рисунка в уравнение g(x)=a+bx+c и получаем систему.

Точки: (-4;1), (-2;5), (0;1).

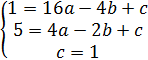
Решаем дальше систему с двумя уравнениями.

óóó

2) Подставляем значения переменных в уравнение.

g(x)=--4x+1

3) Приравниваем оба уравнения и находим x:

-4x+1=-2-2x+4

-2x-3=0

 x=3 или x=-1 так как точка с пересечением при x= -1 уже есть, выбираем вторую.

Ответ: 3

2.4. Корень + прямая.

Задание: на рисунке показаны графики функций вида f(x)=a и g(x)=kx+b, которые пересекаются в точке А. Найдите абсциссу точки А.

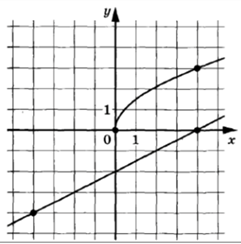
         Решение:

1) Подставим точку (4;3), данную на рисунке в уравнение f(x)=a.

3=a

3=2a

 a=1,5

2) Подставим точки (4;0), (-4;4), данные на рисунке в уравнение g(x)=kx+b. Получаем систему:

óó

Подставим значения переменных в уравнение:

g(x)=0,5x-2

3) Приравняем два уравнения:

0,5x-2=0,5

x-4=3

9x=-8x+16

-17x+16=0

 x=16 или x=1

         Ответ: 16

2.5. Прямая + прямая.

         Задание: на рисунке показаны графики двух линейных функций. Найдите ординату точки пересечения графиков.

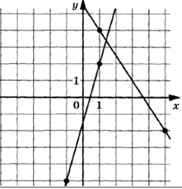
         Решение:

1) Уравнение прямой имеет вид у=kx+b.

2) Подставим точки (1;4), (-2;5) в уравнение прямой и получим систему: 

ó 6=-4k ó k=-1,5; b=5,5

Получаем уравнение: y= -1,5x+5,5

3) Подставим точки (1;2), (-1;-5)в уравнение второй прямой и получим систему:

ó 2b=-3ó b=-1,5; k=3,5

Получаем уравнение: y=3,5x-1,5

4) Приравняем два уравнения и находим абсциссу точки пересечения:

-1,5x+5,5=3,5x-1,5

x=1,4

5) Находим ординату точки пересечения, подставив значение x в уравнение:

 y=3,51,4-1,5

 y=3,4

Ответ: 3,4

3. Дополнительные задания

3.1.

         Здание: на рисунке показан график функции вида f(x)=a+bx+c, где числа a, b и c – целые. Найдите f (-5).

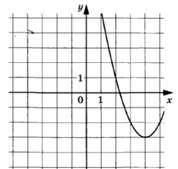
3.2.

         Здание: на рисунке показан график функции вида f(x)=a+bx+c, где числа a, b и c – целые. Найдите f (-9).

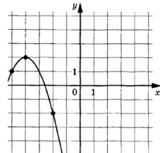
3.3.

Задание: на рисунке изображен график функции вида f (x)= +a.

Найдите f (-8).

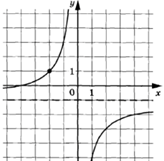
3.4.

Задание: на рисунке изображен график функции вида f (x)= +a.

Найдите при каком значении x значение функции равняется 7.

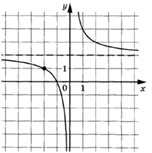
3.5.

Задание: на рисунке показаны графики функций g(x)= kx+b и f(x)=a+bx+c, которые пересекаются в точках А и В. Найдите абсциссу точки В.

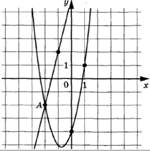
3.6.

Задание: на рисунке показаны графики функций f(x)= 3x+3 и g(x)=a+bx+c, которые пересекаются в точках А (-1;0) и В (; .

Найдите .

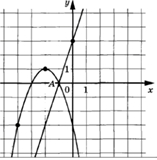
3.7.

Задание: на рисунке изображен график функции вида f(x)=k+ p

Найдите значение x, при котором f(x)=-10.

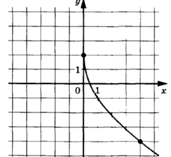
3.8.

Задание: на рисунке показан график функции вида f(x)=k

Найдите f(0,25).

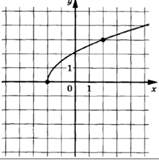
3.9.

Задание: на рисунке показан график функции вида f(x)=b+x. Найдите f (81).

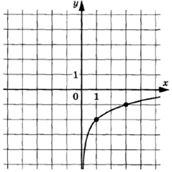
3.10.

Задание: на рисунке показан график функции вида f(x)=b+x. Найдите значение x, при котором f (x)=-2.

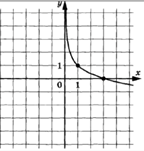
3.11.

Задание: на рисунке показаны графики функций f(x)=2-5x+4 и g(x)=a+bx+c, которые пересекаются в точках А и В. Найдите ординату точки В.

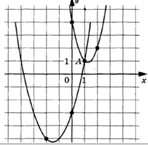
3.12.

Задание: на рисунке показан график функции f(x)=kx+b. Найдите f(-18).

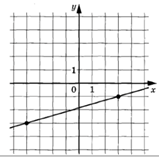
3.13.

Задание: на рисунке показан график функции вида f(x)=a× cosx+ b. Найти a.

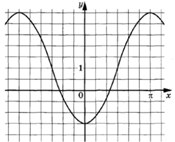
3.14.

Задание: на рисунке показаны графики функций g(x)= ax+b и f(x)=, которые пересекаются в точках А(-2;3) и В (; . Найдите .

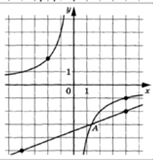
3.15.

Задание: на рисунке показаны графики функций вида f(x)=a и g(x)=kx+b, которые пересекаются в точках А (;  и В(4;5). Найдите .

Ответы:

3.1) 78

3.2) -23

3.3) -0,5

3.4) 0,4

3.5) 2,5

3.6) -15

3.7) 16

3.8) 2,25

3.9) 2

3.10) 27

3.11) 67

3.12) -7

3.13) -2,5

3.14) -0,5

3.15) 1,25