Построение пьезометрических напорных линий. Практическая.

СПб ГБПОУ «Санкт–Петербургский техникум отраслевых технологий финансов и права»

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к выполнению практической работы «Построение пьезометрических напорных линий»

(для студентов специальности 15.02.07

 «Автоматизация технологических процессов и производств»)

Разработал: Савватеев Андрей Сергеевич

Санкт- Петербург

2016

Практическая работа № 4

Построение пьезометрических напорных линий

Цель работы: научиться рассчитывать пьезометрический напор и строить пьезометрические напорные линии.

Теория. Уравнение Бернулли для потока идеальной жидкости:

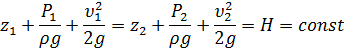
При движении реальной вязкой жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию.

В результате полная удельная энергия жидкости в сечении 1 – 1 будет больше полной удельной энергии в сечении 2 – 2 на величину потерянной энергии.

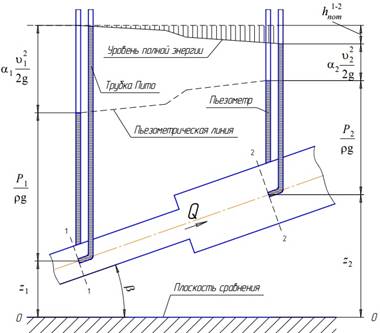
Рис.1

Уравнение Бернулли для реальной жидкости будет иметь вид:

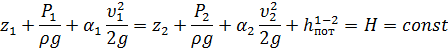
где    – потерянная энергия или потерянный напор

Потерянный напор  складывается из линейных потерь , вызванных силой трения между слоями жидкости, и потерь , вызванных местными сопротивлениями (изменениями конфигурации потока)

Из рис. 1 видно, что по мере движения жидкости от сечения 1—1 до сечения 2 – 2 потерянный напор все время увеличивается (потерянный напор выделен вертикальной штриховкой).

Таким образом, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного напора между сечениями 1—1 и 2—2. Кроме этого в уравнение включены два коэффициента и , которые называются коэффициентами Кориолиса и учитывают неравномерность распределения скоростей в потоке вязкой жидкости. Эти коэффициенты зависят от режима течения жидкости (

.

Уравнение Бернулли для реальной жидкости применяется в технике, например для расчетов водопроводов, нефтепроводов, газопроводов и т.д.

Рассмотрим следующую задачу:

Из бака при постоянном напоре по прямому горизонтальному трубопроводу с вентилем вытекает вода в атмосферу (рис. 2).

Определить расход воды в трубопроводе при полном открытии вентиля и построить пьезометрическую и напорную линии.

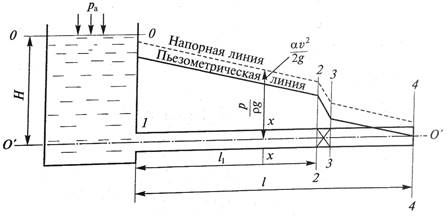
Рис.2

Уравнение Бернулли для сечений 0—0 и 4—4 относительно плоскости сравнения 0’—0’, проведенной через ось трубы:

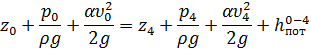
В данном случае

т.к. скорость движения воды в баке много меньше, чем скорость движения воды в трубе, то  

Тогда полный напор:

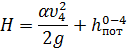
Потерянный напор:

Где  – суммарные потери напора на преодоление местных сопротивлений;  – потери напора на трение по длине трубопровода;         – сумма коэффициентов потерь в местных сопротивлениях.

Или полный напор:

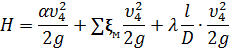
Т.к.  , то

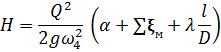
Учитывая, что  , расход жидкости определится:

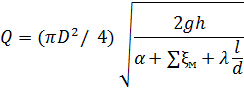
где

Для построения пьезометрической линии определим пьезометрический напор в любом сечении трубопровода:

Уравнение Бернулли для сечений 0—0 и х—х относительно плоскости сравнения 0’—0’:

т.к. пьезометрический напор зависит только от избыточного давления, то для всех сечений считаем  , тогда:

Пьезометрический напор в сечении 1—1:

где

Пьезометрический напор в сечении 2—2 определяется с учетом            

Пьезометрический напор в сечении 3—3 определяется с учетом         

В сечении 4 — 4  и

Исходные данные для расчетов

В качестве исходных данных задаются:

- длина горизонтального трубопровода ;

- диаметр трубопровода ;

- расстояние от начала трубопровода до вентиля ;

- постоянный напор ;

- коэффициент гидравлического трения ;

- коэффициент потерь в вентиле при его полном открытии ;

- коэффициент потерь на входе в трубу ;

- коэффициент неравномерности скоростей (Кориолиса) ;

Исходные данные представлены в таблице.

Порядок проведения расчетов

1.     Найти расход воды в трубопроводе при полном открытии вентиля.

2.     Найти скорость течения воды.

3.     Вычислить пьезометрический напор в сечения 1—1 ; 2—2; 3—3.

4.    Вычислить скоростной (динамический) напор по формуле

Результаты расчетов

1.     Исходные данные и полученные данные занести в таблицу.

2.     Откладывая полученные значения пьезометрического напора в каждом сечении от плоскости сравнения 0’ – 0’, построить пьезометрическую линию (в масштабе).

3.     С учетом равномерности напора в трубопроводе постоянного сечения, построить напорную линию параллельно пьезометрической и выше последней на величину скоростного напора (см. рис. 2).